Algorithm partI 第2节课 Union−Find

发展一个有效算法的具体（一般）过程：

union-find用来解决dynamic connectivity，下面主要讲quick find和quick union及其应用和改进。

基本操作：find/connected queries和union commands

动态连接性问题的场景：

1.1  建立模型（Model the problem）：

关于object：0-N-1

关于连接的等价性：

关于连接块：

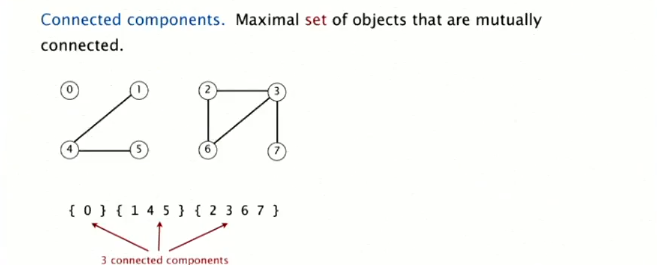
关于基本操作find query和union command：

比如union操作：

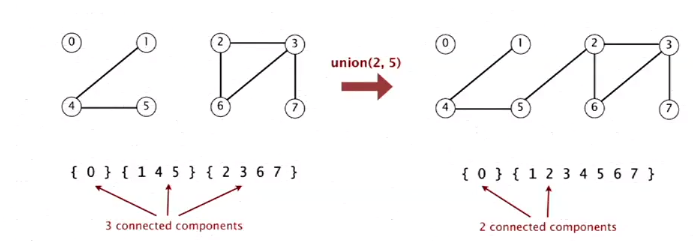
目标：

练习：

答案：C。最后剩下的连接块有{0,5,6}{3,4}{1,2,7,8,9}。

1.2  算法及其改进（Algorithm and improvement）：

1.2.1  Quick Find

实现过程：

 public class QuickFindUF
 {
     private int[] id;

     public QuickFindUF(int N)
     {
         id = new int[N];
         for (int i = 0; i < N; i++)
                 id[i] = i;
     }

     public boolean connected(int p, int q)
     { return id[p] == id[q]; }

     public void union(int p, int q)
     {
         int pid = id[p];
         int qid = id[q];
         for (int i = 0; i < id.length; i++)
             //这里有个约定：
             //p和q联合的时候，所有和p是一个连接块（connected conponents）的点的id都要设置为与id[q]相等
             if (id[i] == pid) id[i] = qid;
     }
 }

各个函数的时间复杂度：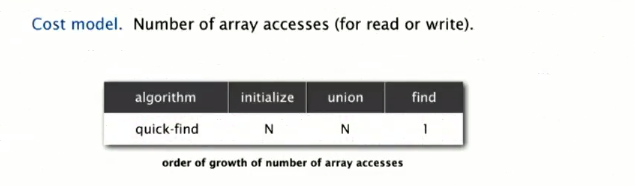

弊端：

对N个实体做N次的union操作，时间复杂度是O(N²)。换言之，Quick find太慢，不适合大量的数据。

练习：

答案：C。最差情况就是除了id[q]，其他元素都要改变。

1.2.2  Quick Union

说明：

实现过程：

 public class QuickUnionUF
 {
     private int[] id;//id[i],节点i的父节点

     public QuickFindUF(int N)
     {
         id = new int[N];
         //划分为N棵子树，每个子树的根节点就是本身
         for (int i = 0; i < N; i++)
                 id[i] = i;
     }

     private int root(int i)//找打i所在子树的根节点
     {
         //如果id[i] == i,说明i是某一棵子树的根节点
         while (i != id[i]) i = id[i];
         return i;
     }

     public boolean connected(int p, int q)
     {
         return root(p) == root(q);
     }

     public void union(int p, int q)//将p所在子树的根节点的父节点设为q所在子树的根节点
     {
         int i = root(p);
         int j = root(q);
         id[i] = j;
     }
 }

各个操作的时间复杂度：注意quick union的union和find是最差情况（例如，形成的子树很高）的时间复杂度。

弊端：

练习：

答案：D。3的根节点是6:3->5->2->6。7的根节点是6:7->1->9->5->2->6。

练习：

答案：C

1.2.3  Weighted quick union

Improvement 1：weighting。为每个树保留track记录树的规模；union的时候将规模小的树的根节点添加为规模大的树的根节点的子节点。主要针对Quick union中容易出现树很高的情况。

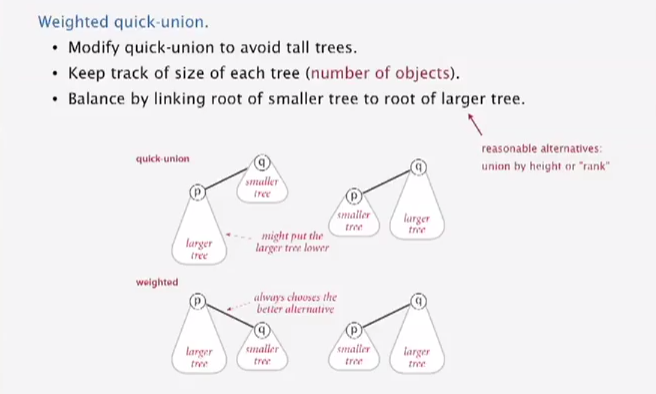
实现过程：

 public class WeightedQuickUnionUF {
     private int[] id,sz;

     public WeightedQuickUnionUF(int N)
     {
         id = new int[N];
         sz = new int[N];//记录以i为根节点的树的节点个数
         for (int i = 0; i < N; i++)
         {
             sz[i] = 1;
             id[i] = i;
         }
     }

     private int root(int i)//和quick union相同
     {
         while (i != id[i]) i = id[i];
         return i;
     }

     public boolean connected(int p, int q)//和quick union相同
     {
         return root(p) == root(q);
     }

     public void union(int p, int q)
     {
         int i = root(p);
         int j = root(q);
         if (i == j) return;
         if (sz[i] < sz[j]){id[i] = j; sz[j] += sz[i];}
         else {id[j] = i; sz[i] += sz[j];}
     }
 }

各个函数的时间复杂度：注意到weighted quick union中的union和connected操作的时间复杂度都是log₂N。

命题：按照Weighted quick union实现的树的任意一个节点的深度不会超过log₂N。

证明：关注任意节点x。

1. 只有当包含x的子树T1作为lower tree被合并的时候，x的深度才有可能增加1。

2. 另一棵树T2，其中sz[T2]>=sz[T1]。

每合并1次，树的规模*2，并且最后的树的规模==N，所以x最多只能增加log₂N次，意味着节点x最后的深度不会超过log₂N。

Weighted quick union和Quick union的比较实例：

Weighted quick union实现结果更加均衡，叶节点到根的距离最大为4，每个节点到根节点的距离的平均要远远小于Quick union的结果。

1.2.4 Weighted quick union with path compressioin

Improvement 2：path compression。就是路径压缩。

实现过程有2种方式：主要区别是root函数的实现。

1. 找到当前点x的根节点后，将x与根节点相连路径上的所有节点的父节点设为根节点。

2. 在寻找当前点x的根节点的过程中，直接将x的父节点设置为x的父节点的父节点。

下面只展示union函数的实现：

方式1：

 private int root(int i)
     {
         if (id[i] == i) return i;//只有指向根节点才返回
         return id[i] = root(id[i]);
     }

方式2：

     private int root(int i)
     {
         while (i != id[i])
         {
             id[i] = id[id[i]];//指向父节点的父节点
             i = id[i];
         }
         return i;
     }

对N个点使用Weighted quick union with path compressioin中的union find操作m次的时间复杂度：

关于lg*的解释：http://stackoverflow.com/questions/2387656/what-is-olog-n/2387669

log* (n)- "log Star n" as known as "Iterated logarithm"

In simple word you can assume log* (n)= log(log(log(.....(log* (n))))

已经证明，union find问题的时间复杂度不可能到O(N)。

练习：

答案：

总结：