替罪羊树（Scapegoat Tree）

入门模板题 洛谷oj P3369

题目描述

　　您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

  1. 插入xx数
  2. 删除xx数(若有多个相同的数，因只删除一个)
  3. 查询xx数的排名(排名定义为比当前数小的数的个数+1+1。若有多个相同的数，因输出最小的排名)
  4. 查询排名为xx的数
  5. 求xx的前驱(前驱定义为小于xx，且最大的数)
  6. 求xx的后继(后继定义为大于xx，且最小的数)

输入格式

　　第一行为n，表示操作的个数,下面n行每行有两个数opt和x，opt表示操作的序号( 1≤opt≤6 )

输出格式

　　对于操作3,4,5,6每行输出一个数，表示对应答案

输入样例

10

1 106465
4 1
1 317721
1 460929
1 644985
1 84185
1 89851
6 81968
1 492737
5 493598

输出样例

106465

84185
492737

数据范围

1.n的数据范围： n≤100000

2.每个数的数据范围： [-10^7, 10^7]

　　网上的资料比较琐碎难懂，之前看了很多资料一直不能理解平衡树（我太弱了）……前几天突然莫名其妙明白了，想写一篇笔记记录一下（乱写一通）。

0x00 二叉查找树

　　要初步弄懂平衡树，首先要知道这是一棵二叉查找树。

　　二叉查找树（Binary Search Tree），当然也可以叫它二叉搜索树，或者二叉排序树（反正都一个意思都是二叉树），它的定义如下：

　　　　或者是一棵空树，或者是具有下列性质的二叉树：

（1）若左子树不空，则左子树上所有结点的值均小于它的根节点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；

　　　　差不多就像下面这幅图一样：

0x01 平衡树的用途

　　在学平衡树这个数据结构前，相信我们一定会先有个问题：平衡树能拿来干什么？

　　网上的很多资料对这一点写得不太明白（也可能是我太弱了），我先试着乱总结一下：
　　　　现在需要一种数据结构，它需要做到以下几点：
　　　　　1. 高效地查询一个序列中某个数的前面和后面的数（a[i-1]和a[i+1]）。
　　　　　2. 高效地知道第i个数是什么（即a[i]）。
　　　　　3. 高效地插入和删除。
　　显然，我们可以用普通数组优秀地完成第1点和第2点，但第3点不能够了。当然，我们也可以用链表，复杂度O(1)优秀地完成第1点和第3点，但是对于第2点，链表的复杂度就达到了不太理想的O(n)。
　　那我们能不能想办法优化一下链表呢？

　　我们可以回头看一下二叉搜索树的定义，然后我们会发现，假设存在一个从1到8的链表（就像下图，win自带画图画的，不太好看）

　　其实它也满足左边小于右边的定义，也可以勉强算是一棵以序号为每个节点的权值的二叉查找树。

　　

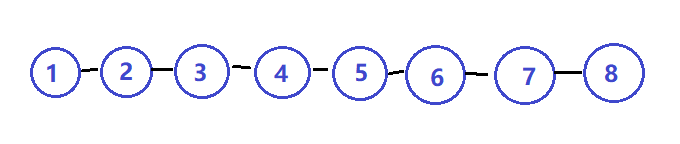
　　但是这样的一棵二叉树是不是很难看很畸形？
　　我们怎么想办法把它变成一棵比较好看的树呢？
　　可以拿笔画画看：
　　我们尝试把中间的节点（4或者5，我选择4）拎出来，然后就变成了这样：

　　

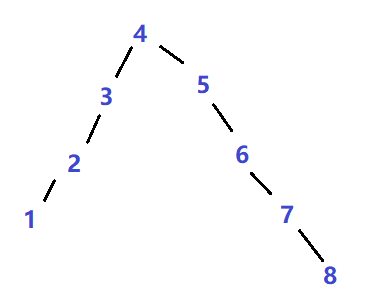
　　是不是好看了一点？有点树的形状了，那我们可以尝试继续把两侧链上的中间节点继续拎出来，不断重复，最终会变成一棵比较好看的树。

　　
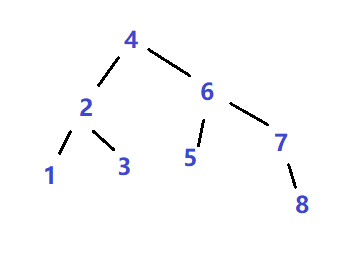
　　这就是平衡二叉树，严格遵守了二叉查找树的定义——左儿子小于右儿子。
　　也许你会有疑问：长成这样的一棵树，怎么做到刚刚链表都不能完全做到的3点要求呢？
　　让我们再看看这棵树：

0x02 查询前驱和后驱
　　对于一个我们已知的节点i，我们先定义与它深度相同的都是它的兄弟节点。

　　那么很显然，i的左兄弟及其子树上的所有节点都比i的左儿子及其子树上的所有节点来得小，且i的左儿子及其子树上的所有点都比i的父亲更大，所以显然，i的前驱要在i的左儿子及其子树上找。

　　同理，仔细观察图，会发现我们所要找的前驱，存在于i的左儿子子树的最右侧，就是i的左儿子的右儿子的右儿子的右儿子的右儿子……（直到最后一个右儿子）

　　这样，我们就可以O(log n)地求出i的前驱了。i的后驱同理。

0x03 查询第i个数

　　前面说过，我们用数的序列编号作为节点的排序权值，所以我们只要像线段树那样从根部开始查一遍就可以了。详细解释：

　　从根结点开始，如果第i个数比当前节点j的序号小，就往左儿子搜，反之右儿子。直到找到第i个数，时间复杂度还是O(log n)。

0x04 插入和删除
　　插在原序列的末尾，所以新节点的编号是n+1。然后我们把这个节点变成根结点的右儿子的右儿子的右儿子……(变成最后一个没有右儿子的节点的右儿子)。

　　删除。其实就是把i节点打个被删除掉的标记（甚至不打也可以）。然后让i的左右儿子之一成为i的父节点的新儿子（就是让某一个儿子取代i节点）。复杂度同O（log n）

　　基本操作差不多就是这样。

　　那么其实还有一个问题：如果操作太多，导致一棵本来平衡的树变成了一条链表，复杂度爆炸，怎么办呢？

0x05 重新建树
　　如果你选择的是替罪羊树，那就是优雅的暴力了。替罪羊树在每个节点上记录子树的节点数size，同时还有一个平衡因子alpha（通常在0.5左右，我选择0.7），当每次更新后，递归回去检查i节点的左右儿子分别乘以平衡因子，是否大于另一个儿子，如果大了，代表这棵树有退化的倾向，赶紧拍平重建（就是把树压成链表，重新建树）。

　　大概就是这样，手机打的好难受，直接上代码好了。

　　(其实我一开始做平衡树时觉得可以用线段树模拟的emmm，就不说了)

　　代码可以配合洛谷的模板题食用

  1. #include <cstdio>
  2. #include <iostream>
  3. using namespace std;
  4. const int INF=;
  5. const int MAX_N=;
  6. const double alpha=0.75;
  7.  
  8. int n;
  9. inline int read(){
  10.     register int ch=getchar(),x=,f=;
  11.     while (ch<''||ch>''){
  12.         if (ch=='-')    f=-;
  13.         ch=getchar();
  14.     } while (ch>=''&&ch<=''){
  15.         x=x*+ch-'';
  16.         ch=getchar();
  17.     } return x*f;
  18. }
  19. struct Tree{
  20.     int fa;
  21.     int size;
  22.     int value;
  23.     int son[];
  24. }tree[MAX_N];
  25. int cnt=;
  26. int root=;
  27. int node[MAX_N];
  28. int sum;
  29.  
  30. bool balance(int x){    //判断是否平衡
  31.     return (double)tree[x].size*alpha>=(double)tree[tree[x].son[]].size&&(double)tree[x].size*alpha>=(double)tree[tree[x].son[]].size;
  32. }
  33. int build(int l,int r){    //重新递归建树
  34.     if (l>r)    return ;
  35.     int mid=(l+r)>>;
  36.     tree[tree[node[mid]].son[]=build(l,mid-)].fa=node[mid],tree[tree[node[mid]].son[]=build(mid+,r)].fa=node[mid];
  37.     tree[node[mid]].size=tree[tree[node[mid]].son[]].size+tree[tree[node[mid]].son[]].size+;
  38.     return node[mid];
  39. }
  40. void recycle(int x){    //把树压成数列
  41.     if (tree[x].son[])    recycle(tree[x].son[]);
  42.     node[++sum]=x;
  43.     if (tree[x].son[])    recycle(tree[x].son[]);
  44. }
  45. void rebuild(int x){
  46.     sum=;
  47.     recycle(x);
  48.     int fa=tree[x].fa,son=(tree[tree[x].fa].son[]==x),now=build(,sum);
  49.     tree[tree[fa].son[son]=now].fa=fa;
  50.     if (x==root)    root=now;
  51. }
  52. void insert(int x){
  53.     int i=root,now=++cnt;    //新节点序号
  54.     tree[now].size=,tree[now].value=x;
  55.     while (true){
  56.         tree[i].size++;
  57.         bool son=(x>=tree[i].value);
  58.         if (tree[i].son[son])    i=tree[i].son[son];
  59.         else{
  60.             tree[tree[i].son[son]=now].fa=i;
  61.             break;
  62.         }
  63.     }
  64.     int flag=;
  65.     for (int j=now;j;j=tree[j].fa)    //logn找不平衡的节点
  66.         if (!balance(j))    flag=j;
  67.     if (flag)    rebuild(flag);    //重建树
  68. }
  69.  
  70. int get_num(int x){
  71.     int i=root;
  72.     while (true){
  73.         if(tree[i].value==x)    return i;
  74.         else    i=tree[i].son[tree[i].value<x];
  75.     }
  76. }
  77. void erase(int x){    //删除
  78.     if (tree[x].son[]&&tree[x].son[]){
  79.         int now=tree[x].son[];
  80.         while (tree[now].son[])    now=tree[now].son[];
  81.         tree[x].value=tree[now].value;
  82.         x=now;
  83.     }
  84.     int son=(tree[x].son[])?tree[x].son[]:tree[x].son[];
  85.     int k=(tree[tree[x].fa].son[]==x);
  86.     tree[tree[tree[x].fa].son[k]=son].fa=tree[x].fa;
  87.     for (int i=tree[x].fa;i;i=tree[i].fa)
  88.         tree[i].size--;
  89.     if (x==root)
  90.         root=son;
  91. }
  92. int get_rank(int x){
  93.     int i=root,ans=;
  94.     while (i)
  95.         if(tree[i].value<x)    ans+=tree[tree[i].son[]].size+,i=tree[i].son[];
  96.         else    i=tree[i].son[];
  97.     return ans;
  98. }
  99. int get_kth(int x){
  100.     int i=root;
  101.     while (true)
  102.         if (tree[tree[i].son[]].size==x-)    return i;
  103.         else if (tree[tree[i].son[]].size>=x)    i=tree[i].son[];
  104.         else    x-=tree[tree[i].son[]].size+,i=tree[i].son[];
  105.     return i;
  106. }
  107. int get_front(int x){
  108.     int i=root,ans=-INF;
  109.     while(i)
  110.         if(tree[i].value<x)    ans=max(ans,tree[i].value),i=tree[i].son[];
  111.         else    i=tree[i].son[];
  112.     return ans;
  113. }
  114. int get_behind(int x){
  115.     int i=root,ans=INF;
  116.     while(i)
  117.         if(tree[i].value>x)    ans=min(ans,tree[i].value),i=tree[i].son[];
  118.         else    i=tree[i].son[];
  119.     return ans;
  120. }
  121. int main(){
  122. //    freopen("test1.in","r",stdin);
  123.     tree[].value=-INF,tree[].size=,tree[].son[]=;
  124.     tree[].value=INF,tree[].size=,tree[].fa=;
  125.     n=read();
  126.     for(int i=,op,x;i<=n;i++){
  127.         op=read(),x=read();
  128.         if(op==)    insert(x);
  129.         if(op==)    erase(get_num(x));
  130.         if(op==)    printf("%d\n",get_rank(x));
  131.         if(op==)    printf("%d\n",tree[get_kth(x+)].value);
  132.         if(op==)    printf("%d\n",get_front(x));
  133.         if(op==)    printf("%d\n",get_behind(x));
  134.     }
  135. }

其他例题

大体上按难度排序？我太弱了也搞不懂。

一.[HNOI2002]营业额统计 （2019.4.10更新）

洛谷oj P2234

　　据说有各种神犇用许多神奇的解法A掉了……但是我这种蒟蒻就先用平衡树练手了。

　　min{|该天以前某一天的营业额-该天营业额|}，即不大于a[i]的最大值和不小于a[i]的最小值，就是寻找a[i]的前驱和后驱，分别减去a[i]取绝对值，再全部加起来，复杂度应该是O(nlogn)。

　　代码：

  1. #include <cstdio>
  2. #include <iostream>
  3. using namespace std;
  4. const int INF=;
  5. const int MAX_N=;
  6. const double alpha=0.75;
  7.  
  8. int n;
  9. inline int read(){
  10.     register int ch=getchar(),x=,f=;
  11.     while (ch<''||ch>''){
  12.         if (ch=='-')    f=-;
  13.         ch=getchar();
  14.     } while (ch>=''&&ch<=''){
  15.         x=x*+ch-'';
  16.         ch=getchar();
  17.     } return x*f;
  18. }
  19. struct Tree{
  20.     int fa;
  21.     int size;
  22.     int value;
  23.     int son[];
  24. }tree[MAX_N];
  25. int cnt=;
  26. int root=;
  27. int node[MAX_N];
  28. int sum;
  29.  
  30. bool balance(register int x){    //判断是否平衡
  31.     return (double)tree[x].size*alpha>=(double)tree[tree[x].son[]].size&&(double)tree[x].size*alpha>=(double)tree[tree[x].son[]].size;
  32. }
  33. inline int build(register int l,register int r){    //重新递归建树
  34.     if (l>r)    return ;
  35.     int mid=(l+r)>>;
  36.     tree[tree[node[mid]].son[]=build(l,mid-)].fa=node[mid],tree[tree[node[mid]].son[]=build(mid+,r)].fa=node[mid];
  37.     tree[node[mid]].size=tree[tree[node[mid]].son[]].size+tree[tree[node[mid]].son[]].size+;
  38.     return node[mid];
  39. }
  40. void recycle(register int x){    //把树压成数列
  41.     if (tree[x].son[])    recycle(tree[x].son[]);
  42.     node[++sum]=x;
  43.     if (tree[x].son[])    recycle(tree[x].son[]);
  44. }
  45. void rebuild(register int x){
  46.     sum=;
  47.     recycle(x);
  48.     int fa=tree[x].fa,son=(tree[tree[x].fa].son[]==x),now=build(,sum);
  49.     tree[tree[fa].son[son]=now].fa=fa;
  50.     if (x==root)    root=now;
  51. }
  52. void insert(register int x){
  53.     int i=root,now=++cnt;    //新节点序号
  54.     tree[now].size=,tree[now].value=x;
  55.     while (true){
  56.         tree[i].size++;
  57.         bool son=(x>=tree[i].value);
  58.         if (tree[i].son[son])    i=tree[i].son[son];
  59.         else{
  60.             tree[tree[i].son[son]=now].fa=i;
  61.             break;
  62.         }
  63.     }
  64.     int flag=;
  65.     for (int j=now;j;j=tree[j].fa)    //logn找不平衡的节点
  66.         if (!balance(j))    flag=j;
  67.     if (flag)    rebuild(flag);    //重建树
  68. }
  69.  
  70. inline int get_front(register int x){
  71.     register int i=root,ans=-INF;
  72.     while(i)
  73.         if(tree[i].value<x)    ans=max(ans,tree[i].value),i=tree[i].son[];
  74.         else    i=tree[i].son[];
  75.     return ans;
  76. }
  77. inline int get_behind(register int x){
  78.     register int i=root,ans=INF;
  79.     while(i)
  80.         if(tree[i].value>x)    ans=min(ans,tree[i].value),i=tree[i].son[];
  81.         else    i=tree[i].son[];
  82.     return ans;
  83. }
  84. bool flag[+];
  85. int result;
  86. int main(){
  87. //  freopen("test1.in","r",stdin);
  88.     tree[].value=-INF,tree[].size=,tree[].son[]=;
  89.     tree[].value=INF,tree[].size=,tree[].fa=;
  90.     n=read();
  91.     int kkk=read();
  92.     result+=kkk;
  93.     insert(kkk);
  94.     flag[kkk]=true;
  95.     for (int i=,a,min,max;i<=n;i++){
  96.         a=read();
  97.         if (flag[a])    continue;
  98.         flag[a]=true;
  99.         insert(a);
  100.         min=get_front(a);
  101.         max=get_behind(a);
  102.         if (min==-INF){
  103.             result+=(max-a);
  104.             continue;
  105.         }
  106.         else if (max==INF){
  107.             result+=(a-min);
  108.             continue;
  109.         }
  110.         result+=(a-min>max-a?max-a:a-min);
  111.     }
  112.     printf("%d",result);
  113.     return ;
  114. }

[学习自百度百科和其他网络资料]

平衡树 替罪羊树（Scapegoat Tree）的更多相关文章

  1. 简析平衡树（一）——替罪羊树 Scapegoat Tree

    前言 平衡树在我的心目中,一直都是一个很高深莫测的数据结构.不过,由于最近做的题目的题解中经常出现"平衡树"这三个字,我决定从最简单的替罪羊树开始,好好学习平衡树. 简介 替罪羊树 ...

  2. [TYVJ1728/BZOJ3224]普通平衡树-替罪羊树

    Problem 普通平衡树 Solution 本题是裸的二叉平衡树.有很多种方法可以实现.这里打的是替罪羊树模板. 此题极其恶心. 前驱后继模块需要利用到rank模块来换一种思路求. 很多细节的地方容 ...

  3. Luogu 3369 / BZOJ 3224 - 普通平衡树 - [替罪羊树]

    题目链接: https://www.lydsy.com/JudgeOnline/problem.php?id=3224 https://www.luogu.org/problemnew/show/P3 ...

  4. bzoj2827: 千山鸟飞绝 平衡树 替罪羊树 蜜汁标记

    这道题首先可以看出坐标没有什么意义离散掉就好了. 然后你就会发现你要每次都更改坐标,而一旦更改受影响的是坐标里的所有数,要是一个一个的改,会不可描述. 所以换个视角,我们要找的是某只鸟所到每个坐标时遇 ...

  5. bzoj 3224: Tyvj 1728 普通平衡树 替罪羊树

    题目链接 您需要写一种数据结构(可参考题目标题),来维护一些数,其中需要提供以下操作:1. 插入x数2. 删除x数(若有多个相同的数,因只删除一个)3. 查询x数的排名(若有多个相同的数,因输出最小的 ...

  6. [luogu3369]普通平衡树(替罪羊树模板)

    解题关键:由于需要根据平衡进行重建,所以不能进行去重,否则无法保证平衡性. #include<cstdio> #include<cstring> #include<alg ...

  7. Bzoj3224 / Tyvj 1728 普通替罪羊树

    Time Limit: 10 Sec  Memory Limit: 128 MBSubmit: 12015  Solved: 5136 Description 您需要写一种数据结构(可参考题目标题), ...

  8. [模板] 平衡树: Splay, 非旋Treap, 替罪羊树

    简介 二叉搜索树, 可以维护一个集合/序列, 同时维护节点的 \(size\), 因此可以支持 insert(v), delete(v), kth(p,k), rank(v)等操作. 另外, prev ...

  9. 在平衡树的海洋中畅游（二）——Scapegoat Tree

    在平衡树的广阔天地中,以Treap,Splay等为代表的通过旋转来维护平衡的文艺平衡树占了觉大部分. 然而,今天我们要讲的Scapegoat Tree(替罪羊树)就是一个特立独行的平衡树,它通过暴力重 ...

随机推荐

  1. Java 设计模式系列（二三）访问者模式(Vistor)

    Java 设计模式系列(二三)访问者模式(Vistor) 访问者模式是对象的行为模式.访问者模式的目的是封装一些施加于某种数据结构元素之上的操作.一旦这些操作需要修改的话,接受这个操作的数据结构则可以 ...

  2. Android应用开发环境的搭建和使用

    主要包括Android SDK.Android开发工具:也包括如何使用Android提供的ADB.DDMS.AAPT.DX等工具,掌握这些工具是开发Android应用的基础技能. 1.Android的 ...

  3. linux上chrome、vlc等程序root不能运行的解决办法

    which vlc 或者 whereis vlc 输入/geteuid,输入i进入输入模式,将geteuid改成getppid,然后ESC,输入wq,保存退出,这样程序root用户就可以运行了. ch ...

  4. PHP性能分析工具：xhprof

    ​phpize的安装   一直想装VLD却一直没装上,因为需要用到phpize,但这个工具大部分机子都没有装,上网搜了一下大部分都是讲phpize的应用没有讲怎么安装. 今天终于搜到了,不过是要在li ...

  5. logback 热修改

    <configuration scan="true" scanPeriod="60 seconds" debug="false"> ...

  6. jQuery-关于Ajax请求async属性的说明及总结

    在jquery的ajax中如果希望实现同步或者异步,我们可以设置async(默认true,表示异步请求),下面举例说明两种请求方式的区别. 1.后台代码 public JsonResult GetDa ...

  7. c# 线程的基本使用

    创建线程 线程的基本操作 线程和其它常见的类一样,有着很多属性和方法,参考下表: 创建线程的方法有很多种,这里我们先从thread开始创建线程 class Program { static void ...

  8. 在.net中创建Access数据库

    static void Main(string[] args) { //环境要求 //安装 access 2003, //引用com组件:Microsoft ADO Ext. 2.8 for DDL ...

  9. 深入了解java虚拟机（JVM） 第十章 字节码指令

    一.字节码指令的含义 Java字节码指令由一个字节长度的,代表某种特定操作含义的数字(操作码)以及其后的零至多个代表此操作所需参数(操作数).此外字节码指令是面向操作数栈的,这里操作数栈在功能上对应实 ...

  10. 2018 OCP 052最新题库及答案-4

    4.For which requirement should you configure shared servers? A) accommodating an increasing number o ...