ng-深度学习-课程笔记-3: Python和向量化(Week2)

1 向量化( Vectorization )

在逻辑回归中，以计算z为例，$ z =  w^{T}+b $，你可以用for循环来实现。

但是在python中z可以调用numpy的方法，直接一句$z = np.dot(w,x) + b$用向量化完成，而且你会发现这个非常快。

ng做了个实验，求两个100万长的一维向量的內积，用向量化花了1.5毫秒，而用for循环计算花了400多毫秒。

所以平常记得用向量化，一定要避免使用for循环，你的代码会快很多。

CPU和GPU都有并行化的指令，有时候叫SIMD( single instruction multiple data )。

如果你使用了这样的内置函数，比如np.function，python的numpy能充分利用并行化去更快的计算。

2 更多向量化的例子( More Vectorization Examples )

平时要避免使用for循环，善用python的numpy库中的内置函数。

比如矩阵A和向量v的內积，可以用np.dot。对一列向量v实施指数运算，可以用np.exp，还有各种np.log，np.abs，np.maxmum( v, 0)等等。

对于 v**2， 1/v这样的操作也要考虑用np里的函数。

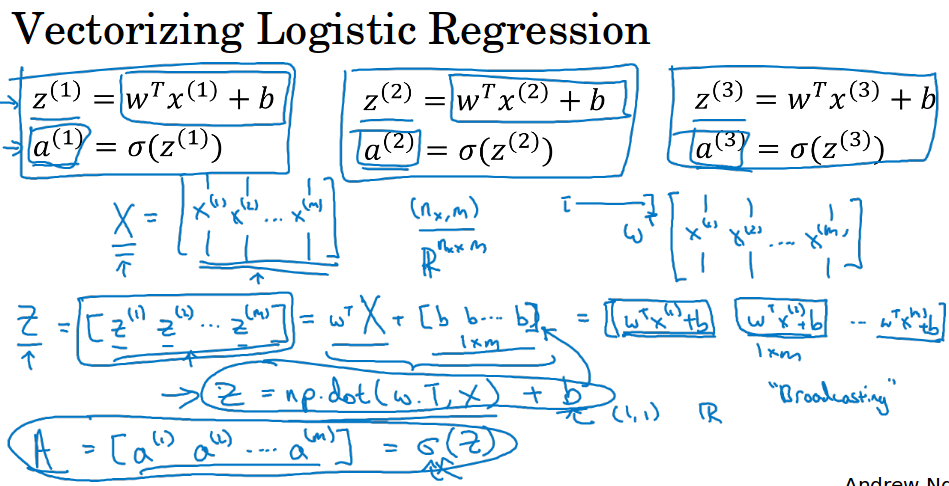
3 向量化逻辑回归( Vectorizing Logistic Regression )

对于逻辑回归的导数计算也应该使用向量化,完全不用for循环。图中给出了向量化的过程。

Z的计算的向量化形式是$z = np.dot(w.T,x) + b$，其中b在这里是一个实数，python在向量和实数相加时，会自动把实数变成一个相同维度的向量再相加。

其中w是n * 1的列向量，w.T是1 * n的列向量，X是n * m的矩阵，结果就是1 * m的向量，最后加上1 * m的b向量，得到1 * m的Z。最后通过sigmoid得到预测值A。

同时还可以利用向量化计算m个数据的梯度，注意是同时计算。下图左边是for循环的实现，右边是向量化的实现。

这里dz是代价函数对z变量的导数，之前推导过等于预测值减去实际值a - y。

dw是代价函数对w的导数，db是代价函数对b的导数，如果不记得了可以翻看上一节课，逻辑回归的内容。

虽然要尽量使用向量化，但是在进行多次梯度下降的迭代还是要用到for循环，这个不可避免。

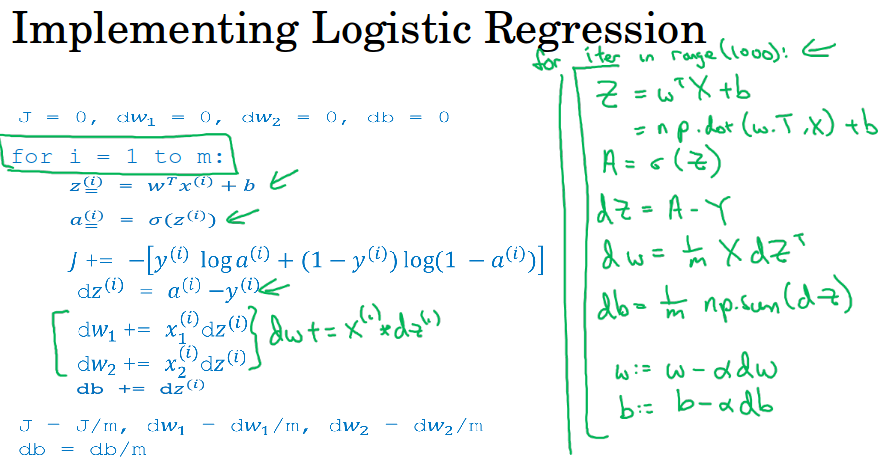
4 python中的广播( python broadcasting)

当你用一个向量加上一个数的时候，python会自动把这个数变成向量再一一相加。

当你用一个m*n的矩阵加（减乘除）上1*n的向量时，python会自动把1*n的向量竖直复制变成m*n再相加。

当你用一个m*n的矩阵加上m*1的向量时，python会自动把m*1的向量水平复制变成m*n再相加。

这是实现神经网络时主要用到的广播，更详细的可以查看numpy文档搜索broadcasting。

对于numpy中的一些用法需要了解，可以帮助你更高效地用矩阵运算来提升程序效率，ng在本节还举了求百分比的例子。

$A.sum(axis=0)$代表竖直求和，如果axis = 1就是水平求和。

5 python / numpy中的向量说明( A note on python/numpy vectors )

numpy和广播使我们可以用一行代码完成很多运算。

但有时可能会引入非常细微的错误，非常奇怪的bug，如果你不熟悉所有的复杂的广播运作方式。

比如你觉得一个行向量和列向量相加应该会报错，但是并不会，而且也不是简单的一一相加。

python这些奇怪的效果有其内在逻辑，如果不熟悉python，你可能会写出奇怪的难以调试的bug。

ng的建议，在实现神经网络的时候不要使用shape为(n,)这样的变量，要用(n,1)。

比如a 的 shape是(5, ) ，当你计算$np.dot(a, a.T)$的时候得到的是一个实数，a和a的转置，它们的shape都是(5, )。

如果a 的 shape是(5, 1)，你计算$np.dot(a, a.T)$的时候得到的就是一个5*5的矩阵。a的shape是( 5, 1)，而a.T的shape是( 1, 5 )。

a.shape = (5, )这是一个秩为1的数组，不是行向量也不是列向量。很多学生出现难以调试的bug都来自秩为1数组。

另外你在代码中做了很多事情后可能不记得或者不确定a是怎样的时候，用$assert( a.shape == (5,1) )$来检查你的矩阵的维度。

如果你得到了(5,) 你可以把它reshape成(5, 1)或(1, 5)，reshape是很快的O(1)复杂度，所以放心大胆的用它，不用担心。