P2610 [ZJOI2012]旅游

题目描述

到了难得的暑假，为了庆祝小白在数学考试中取得的优异成绩，小蓝决定带小白出去旅游~~

经过一番抉择，两人决定将T国作为他们的目的地。T国的国土可以用一个凸N边形来表示，N个顶点表示N个入境/出境口。T国包含N-2个城市，每个城市都是顶点均为N边形顶点的三角形(换而言之，[b]城市组成了关于T国的一个三角剖分[/b])。[b]两人的旅游路线可以看做是连接N个顶点中不相邻两点的线段[/b]。

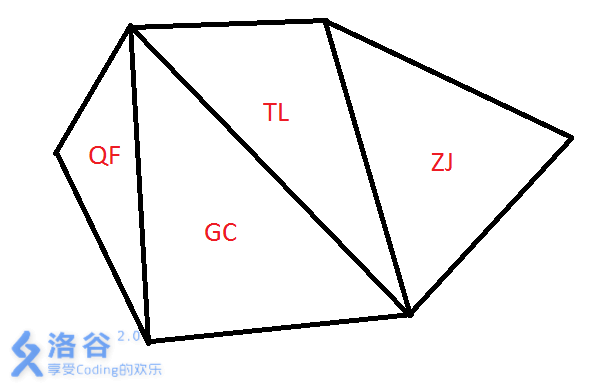
为了能够买到最好的纪念品，小白希望旅游路线上经过的城市尽量多。作为小蓝的好友，你能帮帮小蓝吗？

输入输出格式

输入格式：

每个输入文件中仅包含一个测试数据。

第一行包含两个由空格隔开的正整数N，N的含义如题目所述。

接下来有N-2行，每行包含三个整数 p,q,r，表示该城市三角形的三个顶点的编号(T国的N个顶点按顺时间方向从1至n编号)。

输出格式：

输出文件共包含1行，表示最多经过的城市数目。([b]一个城市被当做经过当且仅当其与线路有至少两个公共点[/b])

输入输出样例

输入样例#1：

6
1 2 4
2 3 4
1 4 5
1 5 6

输出样例#1：

4

说明

对于20%的数据， n<=2000

对于100%的数据， 4<=n<=200000

Solution：

　　本题zyys。

　　我们将能够互相走到的城市之间连边，就能将原题抽象成一棵树，那么最多能走多少个城市就是直径+1了，至于建图直接用map水一下就好了。

代码：

/*Code by 520 -- 8.21*/
#include<bits/stdc++.h>
#define il inline
#define ll long long
#define RE register
#define For(i,a,b) for(RE int (i)=(a);(i)<=(b);(i)++)
#define Bor(i,a,b) for(RE int (i)=(b);(i)>=(a);(i)--)
using namespace std;
typedef pair<int,int> P;
map<P,int> mp;
const int N=;
int n,f[N],ans;
int to[N],net[N],h[N],cnt;
bool vis[N];

int gi(){
    int a=;char x=getchar();
    while(x<''||x>'')x=getchar();
    while(x>=''&&x<='')a=(a<<)+(a<<)+(x^),x=getchar();
    return a;
}

il void add(int u,int v){to[++cnt]=v,net[cnt]=h[u],h[u]=cnt;}

void dp(int u){
    vis[u]=;
    for(RE int i=h[u];i;i=net[i])
        if(!vis[to[i]])
            dp(to[i]),ans=max(ans,f[u]+f[to[i]]+),f[u]=max(f[u],f[to[i]]+);
}

il void init(){
    n=gi()-;
    int a[],tp;
    For(i,,n) {
        a[]=gi(),a[]=gi(),a[]=gi();
        sort(a,a+);
        tp=mp[P(a[],a[])];
        if(tp) add(i,tp),add(tp,i);
        else mp[P(a[],a[])]=i;
        tp=mp[P(a[],a[])];
        if(tp) add(i,tp),add(tp,i);
        else mp[P(a[],a[])]=i;
        tp=mp[P(a[],a[])];
        if(tp) add(i,tp),add(tp,i);
        else mp[P(a[],a[])]=i;
    }
    dp();
    cout<<ans+;
}

int main(){
    init();
    return ;
}