【讲●解】KMP算法

术语与规定

为了待会方便，所以不得不做一些看起来很拖沓的术语，但这些规定能让我们更好地理解$KMP$甚至$AC$自动机。

字符串匹配形式化定义如下：

假设文本是一个长度为$n$的数组$T[1...n]$，而模式是一个长度为$m$的数组$P[1...m]$，其中$m<=n$，进一步假设构成$P$和$T$的元素都是来自一个有限字母集$\Sigma$的字符。例如：$\Sigma=${$0,1$}或者$\Sigma=${$a,b,...,z$}。字符数组通常称为字符串。

我们用$\Sigma^*$表示所有有限长度字符串的集合，该字符串由字母表$\Sigma$中的字符组成。特别地，长度为$0$的空字符用$\varepsilon$表示，也属于$\Sigma^*$。一个字符串$x$的长度用$|x|$表示。两个字符串$x$和$y$的连结用$xy$来表示，长度为$|x|+|y|$，由$x$的字符串后接$y$的字符串构成。

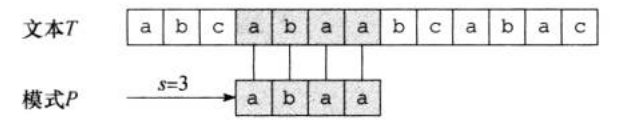
如果$0<=s<=n-m$，并且$T[s+1...s+m]=P[1...m]$（即如果$T[s+j]=P[j]$，其中$1<=j<=m$），那么称模式$P$在文本$T$中出现，且偏移为$s$。如果$P$在$T$中以偏移$s$存在，那么称$s$是有效偏移；否则，称它为无效偏移。如图一，$s=3$就是一个有效位移。根据此约定，字符串匹配问题就可以变成：对于模式串$P$找出所有文本串$T$的有效偏移。

如果对于某个字符串$y\in\Sigma^*$有$x=wy$，则称字符串$w$是字符串$x$的前缀，记作$w\sqsubset x$。类似的，我们也可以定义后缀符号：若$x=yw$，则称字符串$w$是字符串$x$的后缀，记作$w\sqsupset x$。可以看出：如果$w\sqsubset x$，则$|w|<=|x|$。特别地，空字符串$\varepsilon$同时是任何一个字符串的前缀和后缀。

（想一想我们为什么要引入$\sqsupset$和$\sqsubset$符号。）

如果不做特殊说明，我们约定认为$a$为一个字符，即长度为$1$的字符串。

为了使符号简洁，我们把模式$P$的由前$k$个字符组成的前缀$P[1...k]$记作$P_k$，$P_m=P$，采用这种记号，我们又能够把字符串匹配问题表述成：

找到所有偏移$s(0<=s<=n-m)$，使得$P\sqsupset T_{s+m}$。

首先，我们考虑朴素算法的操作过程

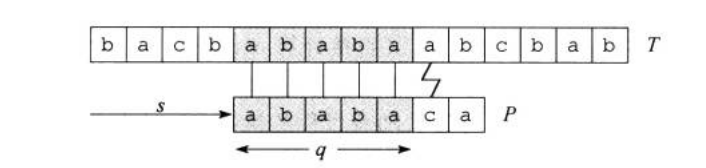
图一展示了一个针对文本串$T$模式串$P$的的一个特定位移$s$。它已经匹配到了$P_q$，在$q+1$的位置与文本串$T$失配。

按照朴素算法的操作，我们这时应进行$s'=s+1，q=1$的操作，把文本串的匹配指针左移到$s'+1$位，模式串$P$匹配指针移回$1$位，从头开始匹配。可这样时间开销是个很大的问题。

那怎么办呢？

我们能不能不把文本串的指针向左移，而直接把模式串的匹配指针对准下一个可能的匹配位置上，即只移动模式串$P$呢？

答案是可以的。

别忘了我们已经匹配好了$P_q$，这意味着我们已经知道了$T[s+1...s+q]=P[1...q]$，如果能把这东西给利用起来那该多好啊！

怎么用呢？

于是，$KMP$算法就来了。

KMP主体

还是用图二。

$q=5$个字符已经匹配成功的信息确定了相应的文本字符。已知的这$p$个文本字符使我们能够立即确认某些偏移一定是无效的。就比如上面所说的$s'=s+1$。

KMP算法思想便是利用已经匹配上的字符信息，使得模式串的指针回退的字符位置能将主串与模式串已经匹配上的字符结构重新对齐。

什么意思？

假设我们存在这样一个映射函数，先把它理解成一个小黑盒。当我们在模式串$q+1$的位置上失配时，它能跳到$P$串的某一位置$k$（注意是$P$串），即$k=next[q]$使得$P_{k}$与先前已匹配的$q$个字符的文本串不发生冲突，然后再比较$k+1$的位置是否与当前文本串指针匹配，如果不能，那继续找$next[k]$；如果能，那就成功匹配一位，进行下一位的匹配。这样，文本串的指针只会向右移而不会向左移。那么这个匹配程序就很好实现了。

这里直接给出伪代码：

KMP-MATCHER(T,P)

  n = T.length

  m = P.length

  next = COMPUTE-PREFIX-FUNCTION(P)//这里的next就是那个小黑盒

  q = 0

  for i=1 to n

    while q>0 and P[q+1]!=T[i]

      q = next[q]

    if P[q+1] == T[i]

      q = q+1

    if q == m

      print "Pattern occurs with shift" i-m

      q = next[q]//匹配成功后肯定要往回走啊

这就是$KMP$算法的主体！

（仔细回味下）

那我们怎么求这个$next[q]$呢？

我们来观察它的性质。

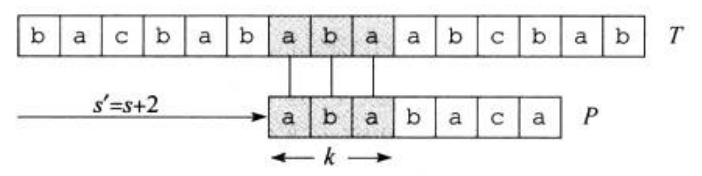
如图三，根据$q=5$个字符已经完全匹配，那么图中的$P_k\sqsupset T[s+1...s+q]$，且$k$是满足此条件的最大值，我们直接可以从$P[k+1]$开始与文本串匹配。也就是说，这里的$k$就是我们要找的$next[q]$。

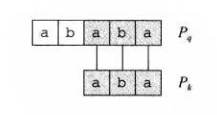
在图四中，我们把$P_q$和$P_k$单独拿了出来，你发现了什么？

$P_k\sqsupset P_q$！

可以看出$k$是满足条件的最大值，也就是说：

\[next[q]=max\{k:k<q且P_k\sqsupset P_q\}
\]

为什么会是这样呢？

我们想要直接在$k+1$位开始匹配，就得保证$P_k\sqsupset T[s+1...s+q]$，虽然我们在$q+1$位失配，但我们已经知道了$P_q = T[s+1...s+q]$，所以即有$P_k\sqsupset P_q$。

那为什么我们会要求$k$为满足条件的最大值呢？

这里先简单理解，$k$为最大值也就包含了$k$为更小值的情况。

那么，这个$next$我们就把它视为$P$的前缀函数。

那么，怎么来求这个$next$呢？

首先，我们肯定能想到一种朴素算法，这里就不细说了，因为用朴素算法还不如敲个$O((n-m+1)m)$的匹配算法呢。。。

那我们怎么来优化求法呢？

同样假设，对于一个模式串$P$，我们已经知道了$next[1...q-1]$，现在，我们来计算$next[q]$。其中，$next[q-1]=k$。

引理1：当$P[k+1]=P[q]$时，可得$next[q]=k+1$。（前缀函数延续性引理）

证明：

因为：$next[q-1]=k$ 即 $P_k\sqsupset P_{q-1}$。

若字符$P[k+1]=P[q]$，则$P_{k+1}\sqsupset P_q$。

所以：$next[q]=k+1$。

证毕。

引理2：若$next[q-1]$的最大候选项为$k$，即$next[q-1]=k$，则它的次大候选项为$next[k]$，次次大为$next[next[k]]$......（前缀函数迭代引理）

证明：（反证法）

若存在$k_0$使得$P_{k_0}\sqsupset P_{q-1}$且$next[k]<k_0<k$。

因为：$next[q-1]=k$，即$P_k\sqsupset P_{q-1}$。

又因为：$k_0<k$。

所以：$P_{k_0}\sqsupset P_k$。

即：$next[k]=k_0$。

这与$next[k]<k_0$矛盾。

所以假设不成立。

证毕。

后面的依次类推。

由前两个引理可以看出，$next[q]$可能的候选项为：$next[q-1]+1$，$next[next[q-1]]+1$......而易知，$next[1]=0$。

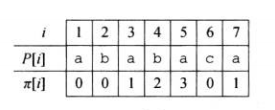
于是，我们便可以高效计算$next$数组。

COMPUTE-PREFIX-FUNCTION(P)

  m = P.length

  pi[1] = 0

  k = 0

  for q=2 to m

    while k>0 and P[k+1]!=P[q]

      k = pi[k]

    if P[k+1] == P[q]

      k = k+1

      pi[q] = k

是不是和KMP-MATCHER很像？

其实，实质上，KMP算法求前缀函数的过程就是模式串的自我匹配。

为什么我们先说$KMP$算法的主体再谈$next$的计算？其实这是从两种角度出发认识$KMP$。讲解主体的时候我们采用了假设法，这是一种十分感性的认知，比较好懂。在讲解$next$的计算时，我们引用了一些数学思维来帮助我们更加理解$KMP$。大家可以看出，实质上，$KMP$主体和$next$的计算是几乎一样的逻辑。

至此，$KMP$算法原理的讲解到此结束。

参考文献

算法导论
算法进阶指南
详解KMP
剖析KMP
字符串匹配算法集合