微软2016校园招聘在线笔试 B Professor Q's Software [ 拓扑图dp ]

传送门

题目2 : Professor Q's Software

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

Professor Q develops a new software. The software consists of N modules which are numbered from 1 to N. The i-th module will be started up by signal S_i. If signal S_i is generated multiple times, the i-th module will also be started multiple times. Two different modules may be started up by the same signal. During its lifecircle, the i-th module will generate K_i signals: E₁, E₂, ..., E_Ki. These signals may start up other modules and so on. Fortunately the software is so carefully designed that there is no loop in the starting chain of modules, which means eventually all the modules will be stoped. Professor Q generates some initial signals and want to know how many times each module is started.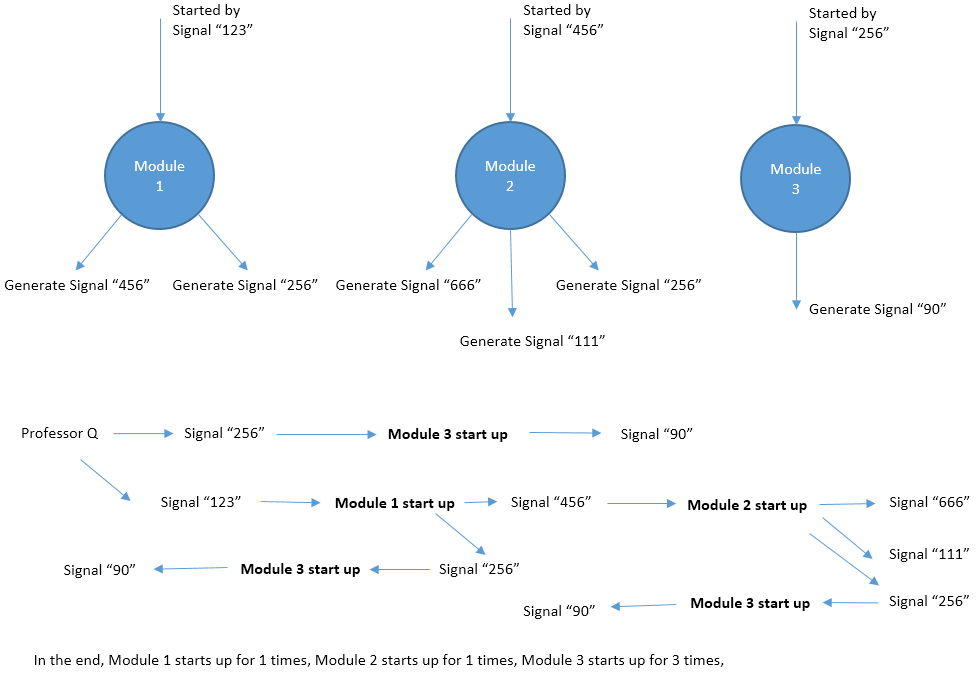

输入

The first line contains an integer T, the number of test cases. T test cases follows.

For each test case, the first line contains contains two numbers N and M, indicating the number of modules and number of signals that Professor Q generates initially.

The second line contains M integers, indicating the signals that Professor Q generates initially.

Line 3~N + 2, each line describes an module, following the format S, K, E₁, E₂, ... , E_K. S represents the signal that start up this module. K represents the total amount of signals that are generated during the lifecircle of this module. And E₁ ... E_K are these signals.

For 20% data, all N, M <= 10
For 40% data, all N, M <= 10³
For 100% data, all 1 <= T <= 5, N, M <= 10⁵, 0 <= K <= 3, 0 <= S, E <= 10⁵.

Hint: HUGE input in this problem. Fast IO such as scanf and BufferedReader are recommended.

输出

For each test case, output a line with N numbers Ans₁, Ans₂, ... , Ans_N. Ans_i is the number of times that the i-th module is started. In case the answers may be too large, output the answers modulo 142857 (the remainder of division by 142857).

样例输入

3
3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90
3 1
100
100 2 200 200
200 1 300
200 0
5 1
1
1 2 2 3
2 2 3 4
3 2 4 5
4 2 5 6
5 2 6 7

样例输出

1 1 3
1 2 2
1 1 2 3 5

题意：

一个有向无环图，初始访问某些点，访问过的点会沿着能连的边一直走到底，问，最后每个点分别被访问了几次。

题解：

来自天猫的思路。

拓扑图dp。一个很好的思路~~~

从根节点开始，如果某个节点访问了，它的所有儿子节点访问数+1。

由于是按照拓扑顺序来处理的（并且没有环），所以，在继续对儿子的儿子处理时，不会再出现儿子节点再增加访问数。

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <cmath>
 #include <string>
 #include <cstdlib>
 #include <algorithm>
 #include <map>
 #include <set>
 #include <utility>
 #include <vector>
 #include <queue>

 using namespace std;

 typedef pair<int,int> PII;
 typedef pair<int,PII> PIII;

 #define LL long long
 #define ULL unsigned long long
 #define m_p make_pair
 #define l_b lower_bound
 #define p_b push_back
 #define w1 first
 #define w2 second
 #define maxlongint 2147483647
 #define biglongint 2139062143

 const int maxn=;
 const int A=;

 int TT,N,M,o,sc,tj;
 vector<int> F[maxn];
 int c[maxn],a[maxn],ans[maxn],vis[maxn],dp[maxn],inp[maxn];

 void dfs(int s)
 {
     if (vis[s]==) return;
     vis[s]=;
     for (int i=;i<F[s].size();i++)
         dfs(F[s][i]);
     ++o,ans[o]=s;
 }

 int main()
 {
     scanf("%d",&TT);
     for (int gb=;gb<=TT;gb++)
     {
         scanf("%d %d",&N,&M);
         for (int i=;i<=M;i++) scanf("%d",&c[i]);
         memset(inp,,sizeof(inp));
         for (int i=;i<=A;i++) F[i].clear();
         for (int i=;i<=N;i++)
         {
             scanf("%d",&a[i]);
             scanf("%d",&sc);
             for (int j=;j<=sc;j++)
             {
                 scanf("%d",&tj);
                 if (tj>A) continue;
                 F[a[i]].p_b(tj);
                 ++inp[tj];
             }
         }
         o=;
         memset(vis,,sizeof(vis));
         for (int i=;i<=A;i++)
             if (inp[i]==) dfs(i);
         memset(dp,,sizeof(dp));
         for (int i=;i<=M;i++) dp[c[i]]++;
         for (int i=A+;i>=;i--)
         {
             sc=ans[i];
             for (int j=;j<F[sc].size();j++)
                 dp[F[sc][j]]+=dp[sc],dp[F[sc][j]]%=;
         }
         for (int i=;i<N;i++) printf("%d ",dp[a[i]]);printf("%d\n",dp[a[N]]);
     }
     return ;
 }