BZOJ 1509[NOI 2003]逃学的小孩 树形dp

1509: [NOI2003]逃学的小孩

Time Limit: 5 Sec  Memory Limit: 64 MB
Submit: 995  Solved: 505
[Submit][Status][Discuss]

Description

Input

第一行是两个整数N（3  N  200000）和M，分别表示居住点总数和街道总数。以下M行，每行给出一条街道的信息。第i+1行包含整数Ui、Vi、Ti（1Ui, Vi  N，1  Ti  1000000000），表示街道i连接居住点Ui和Vi，并且经过街道i需花费Ti分钟。街道信息不会重复给出。

Output

仅包含整数T，即最坏情况下Chris的父母需要花费T分钟才能找到Chris。

Sample Input

4 3
1 2 1
2 3 1
3 4 1

Sample Output

4

 

题解：

这道题目只能讲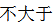这个很关键，所以记录第二长的边乘以两倍，就OK了

什么树形dp，没有的。

 #include<cstdio>
 #include<algorithm>
 #include<cmath>
 #include<iostream>
 #include<cstring>
 #define N 200007
 #define ll long long
 using namespace std;
 
 int n,m;ll ans;
 int cnt,head[N],next[N*],rea[N*];ll val[N*];
 bool boo[N];
 struct Node
 {
     int pos;ll dis;
 }a[N][];
 
 bool cmp(Node x,Node y){return x.dis>y.dis;}
 void add(int u,int v,int fee){next[++cnt]=head[u],head[u]=cnt,rea[cnt]=v,val[cnt]=fee;}
 void dfs_init(int u,int fa)
 {
     for (int i=head[u];i!=-;i=next[i])
     {
         int v=rea[i],fee=val[i];
         if (v==fa) continue;
         dfs_init(v,u);
         a[u][].pos=v;
         a[u][].dis=a[v][].dis+fee;
         sort(a[u]+,a[u]++,cmp);
     }
     ans=max(ans,a[u][].dis+*a[u][].dis+a[u][].dis);
 }
 void dfs_solve(int u)
 {
     boo[u]=;
     for (int i=head[u];i!=-;i=next[i])
     {
         int v=rea[i],fee=val[i];
         if (boo[v])
         {
             if (a[v][].pos!=u) a[u][].dis=a[v][].dis+fee;
             else a[u][].dis=a[v][].dis+fee;
             a[u][].pos=v;
             sort(a[u]+,a[u]++,cmp);
             break;
         }
     }
     ans=max(ans,a[u][].dis+*a[u][].dis+a[u][].dis);
     for (int i=head[u];i!=-;i=next[i])
     {
         int v=rea[i];
         if (!boo[v]) dfs_solve(v);
     }
 }
 int main()
 {
     memset(head,-,sizeof(head));
     scanf("%d%d",&n,&m);
     int x,y,z;
     for (int i=;i<=m;i++)
     {
         scanf("%d%d%d",&x,&y,&z);
         add(x,y,z),add(y,x,z);
     }
     dfs_init(,-);
     dfs_solve();
     printf("%lld\n",ans);
 }