(转载)Catalan数——卡特兰数

Catalan数——卡特兰数 
今天阿里淘宝笔试中碰到两道组合数学题，感觉非常亲切，但是笔试中失踪推导不出来
后来查了下，原来是Catalan数。悲剧啊，现在整理一下

一、Catalan数的定义令h(1)=1，Catalan数满足递归式：h(n) = h(1)*h(n-1) + h(2)*h(n-2) + ... + h(n-1)h(1)，n>=2该递推关系的解为：h(n) = C(2n-2,n-1)/n，n=1,2,3,...（其中C(2n-2,n-1)表示2n-2个中取n-1个的组合数）

问题描述:
12个高矮不同的人，排成两排，每排必须是从矮到高排列，而且第二排比对应的第一排的人高，问排列方式有多少种？
这个笔试题，很YD，因为把某个递推关系隐藏得很深。

问题分析:
我们先把这12个人从低到高排列,然后,选择6个人排在第一排,那么剩下的6个肯定是在第二排.
用0表示对应的人在第一排,用1表示对应的人在第二排,那么含有6个0,6个1的序列,就对应一种方案.
比如000000111111就对应着
第一排：0 1 2 3 4 5
第二排：6 7 8 9 10 11
010101010101就对应着
第一排：0 2 4 6 8 10
第二排：1 3 5 7 9 11
问题转换为，这样的满足条件的01序列有多少个。
观察1的出现，我们考虑这一个出现能不能放在第二排，显然，在这个1之前出现的那些0,1对应的人
要么是在这个1左边，要么是在这个1前面。而肯定要有一个0的，在这个1前面，统计在这个1之前的0和1的个数。
也就是要求，0的个数大于1的个数。
OK，问题已经解决。
如果把0看成入栈操作，1看成出栈操作，就是说给定6个元素，合法的入栈出栈序列有多少个。
这就是catalan数,这里只是用于栈，等价地描述还有，二叉树的枚举、多边形分成三角形的个数、圆括弧插入公式中的方法数，其通项是c(2n, n)/(n+1)。

在<<计算机程序设计艺术>>，第三版，Donald E.Knuth著，苏运霖译，第一卷，508页，给出了证明:
问题大意是用S表示入栈，X表示出栈，那么合法的序列有多少个(S的个数为n)
显然有c(2n, n)个含S，X各n个的序列，剩下的是计算不允许的序列数(它包含正确个数的S和X，但是违背其它条件)。
在任何不允许的序列中，定出使得X的个数超过S的个数的第一个X的位置。然后在导致并包括这个X的部分序列中，以S代替所有的X并以X代表所有的S。结果是一个有(n+1)个S和(n-1)个X的序列。反过来，对一垢一种类型的每个序列，我们都能逆转这个过程，而且找出导致它的前一种类型的不允许序列。例如XXSXSSSXXSSS必然来自SSXSXXXXXSSS。这个对应说明，不允许的序列的个数是c(2n, n-1)，因此an = c(2n, n) - c(2n, n-1)。

验证：其中F表示前排，B表示后排，在枚举出前排的人之后，对应的就是后排的人了，然后再验证是不是满足后面的比前面对应的人高的要求。

#include <iostream>
using namespace std;

int bit_cnt(int n)
{
    int result = ;
    for (; n; n &= n-, ++result);
    return result;
}

int main(void)
{
    int F[], B[];
    int i,j,k,state,ok,ans = ;
    for (state = ; state < ( << ); ++state)
    {
        if (bit_cnt(state) == )
        {
            i = j = ;
            for (int k = ; k < ; ++k)
            {
                if(state&(<<k))
                    F[i++] = k;
                else
                    B[j++] = k;
            }
            ok = ;
            for (k = ; k < ; ++k)
            {
                if (B[k] < F[k])
                {
                    ok = ;
                    break;
                }
            }
            ans += ok;
        }
    }
    cout << ans << endl;
    return ;
}

结果：132

而c(12, 6)/7 = 12*11*10*9*8*7/(7*6*5*4*3*2) = 132

注意：c(2n, n)/(n+1) = c(2n, n) - c(2n, n-1)
估计出题的人也读过<<计算机程序艺术>>吧。

PS：
另一个很YD的问题:
有编号为1到n(n可以很大，不妨在这里假定可以达到10亿)的若干个格子，从左到右排列。
在某些格子中有一个棋子，不妨设第xi格有棋子(1<=i<=k, 1<=k<=n)
每次一个人可以把一个棋子往左移若干步，但是不能跨越其它棋子，也要保证每个格子至多只有一个棋子。
两个人轮流移动，移动不了的为输，问先手是不是有必胜策略。

三、Catalan数的典型应用：

1、括号化问题。矩阵链乘： P=A1×A2×A3×……×An，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

一个有n个X和n个Y组成的字串，且所有的部分字串皆满足X的个数大于等于Y的个数。以下为长度为6的dyck words:
                            XXXYYY     XYXXYY    XYXYXY    XXYYXY    XXYXYY
    将上例的X换成左括号，Y换成右括号，Cn表示所有包含n组括号的合法运算式的个数：
                         ((()))     ()(())      ()()()      (())()      (()())

2、将多边行划分为三角形问题。将一个凸多边形区域分成三角形区域(划分线不交叉)的方法数?

类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

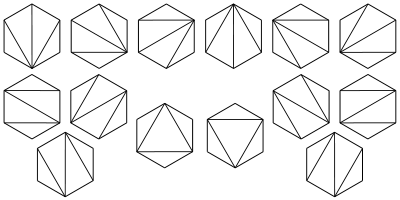
3、出栈次序问题。一个栈(无穷大)的进栈序列为1、2、3、...、n，有多少个不同的出栈序列?
类似：有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

类似：一位大城市的律师在他住所以北n个街区和以东n个街区处工作，每天她走2n个街区去上班。如果他从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？

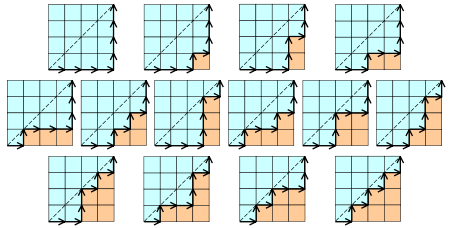
分析：对于每一个数来说，必须进栈一次、出栈一次。我们把进栈设为状态‘1’，出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b)，因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数，1的累计数不小于0的累计数的方案种数。

4、给顶节点组成二叉树的问题。
　　给定N个节点，能构成多少种形状不同的二叉树？
　　(一定是二叉树！先取一个点作为顶点，然后左边依次可以取0至N-1个相对应的，右边是N-1到0个，两两配对相乘，就是h(0)*h(n-1) + h(2)*h(n-2) + ...... + h(n-1)h(0)=h(n))   （能构成h（N）个）

在2n位二进制数中填入n个1的方案数为c(2n,n)，不填1的其余n位自动填0。从中减去不符合要求（由左而右扫描，0的累计数大于1的累计数）的方案数即为所求。
       不符合要求的数的特征是由左而右扫描时，必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数，此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换，使之成为n-m个0和n-m-1个1，结果得1个由n+1个0和n-1个1组成的2n位数，即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
       反过来，任何一个由n+1个0和n-1个1组成的2n位二进制数，由于0的个数多2个，2n为偶数，故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换，使之成为由n个0和n个1组成的2n位数，即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。

因而不合要求的2n位数与n＋1个0，n－1个1组成的排列一一对应。

显然，不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=1/(n+1)*c(2n,n)。
（这个公式的下标是从h(0)=1开始的）