花纹的生成可以使用贴图的方式，同样也可以使用方程，本文列出了几种常用曲线的方程式，以取代贴图方式完成特定花纹的生成。

注意极坐标的使用.................

前面部分基础资料，参考：Python：Matplotlib 画曲线和柱状图（Code）

Pyplot教程：https://matplotlib.org/gallery/index.html#pyplots-examples

顾名思义，蝴蝶曲线（Butterfly curve ）就是曲线形状如同蝴蝶。蝴蝶曲线如图所示，以方程描述，是一条六次平面曲线。如果大家觉得这个太过简单，别着急，还有第二种。如图所示，以方程描述，这是一个极坐标方程。通过改变这个方程中的变量θ，可以得到不同形状与方向的蝴蝶曲线。如果再施以复杂的组合和变换，我们看到的就完全称得上是一幅艺术品了。

Python代码：

import numpy as np

import matplotlib.pyplot as plt

import os,sys,caffe

import matplotlib as mpl

from mpl_toolkits.mplot3d import Axes3D  #draw lorenz attractor

# %matplotlib inline

from math import sin, cos, pi

import math

def mainex():

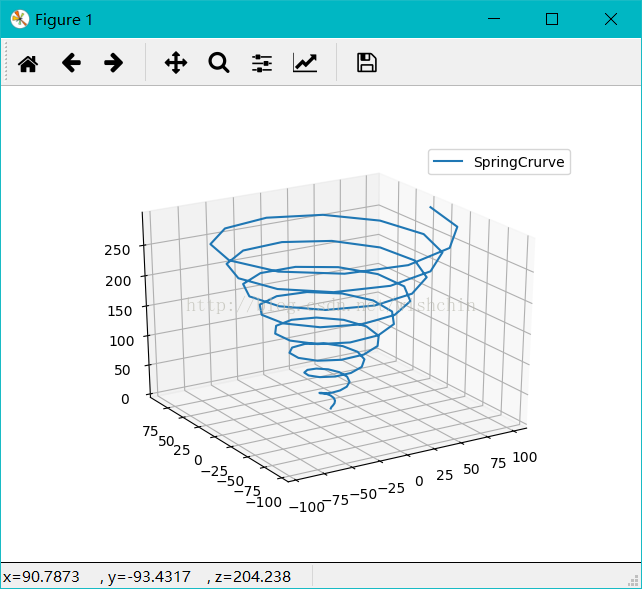
    #drawSpringCrurve();#画柱坐标系螺旋曲线

    #HelicalCurve();#采用柱坐标系#尖螺旋曲线

    #Votex3D();

    #phoenixCurve();

    #ButterflyCurve();

    #ButterflyNormalCurve();

    #dicareCurve2d();

    #WindmillCurve3d();

    #HelixBallCurve();#球面螺旋线

    #AppleCurve();

    #HelixInCircleCurve();#使用scatter，排序有问题

    seperialHelix();

def drawSpringCrurve():

    #碟形弹簧

    #圓柱坐标

    #方程：

    #import matplotlib as mpl

    #from mpl_toolkits.mplot3d import Axes3D

    #import numpy as np

    #import matplotlib.pyplot as plt

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    # Prepare arrays x, y, z

    #theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)

    #z = np.linspace(-2, 2, 100)

    #r = z**2 + 1

    t = np.arange(0,100,1);

    r = t*0 +20;

    theta = t*3600 ;

    z = np.arange(0,100,1);

    for i in range(100):

        z[i] =(sin(3.5*theta[i]-90))+24*t[i];

    x = r * np.sin(theta);

    y = r * np.cos(theta);

    ax.plot(x, y, z, label='SpringCrurve');

    ax.legend();

    plt.show();

def HelicalCurve():

    #螺旋曲线#采用柱坐标系

    t = np.arange(0,100,1);

    r =t ;

    theta=10+t*(20*360);

    z =t*3;

    x = r * np.sin(theta);

    y = r * np.cos(theta);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='HelicalCurve');

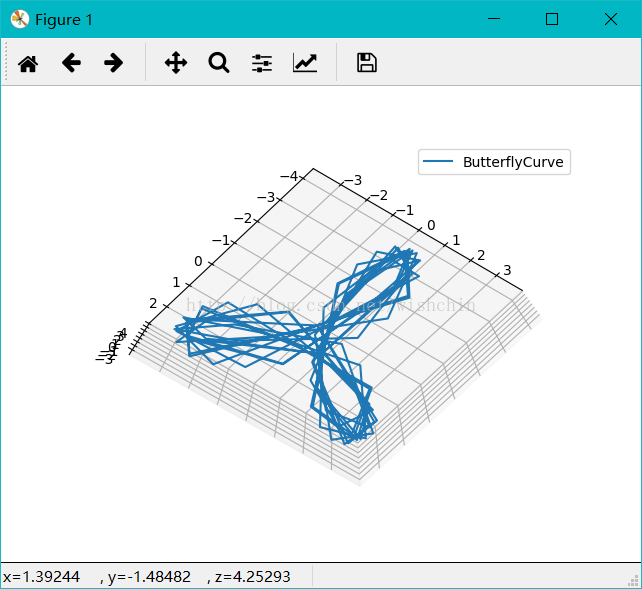
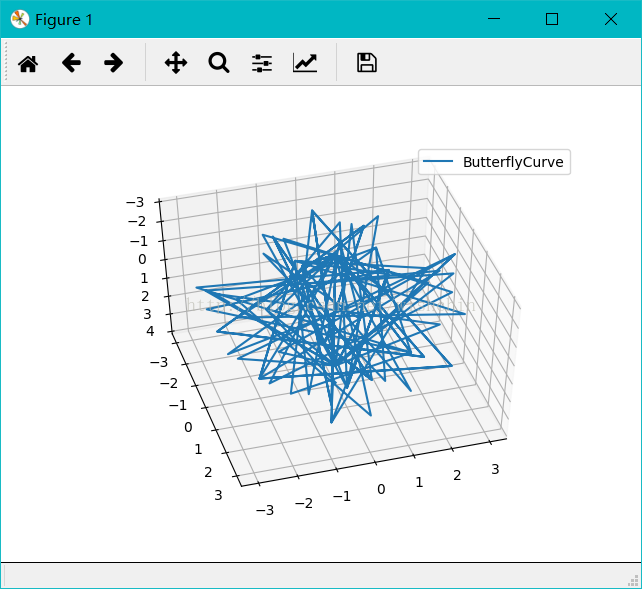
    ax.legend();

    plt.show();

def ButterflyCurve():

    #蝶形曲线，使用球坐标系#或许公式是错误的，应该有更加复杂的公式

    t = np.arange(0,4,0.01);

    r = 8 * t;

    theta = 3.6 * t * 2*1 ;

    phi   = -3.6 * t * 4*1;

    x = t*1;

    y = t*1;

    #z = t*1;

    z =0

    for i in range(len(t)):

        x[i] = r[i] * np.sin(theta[i])*np.cos(phi[i]);

        y[i] = r[i] * np.sin(theta[i])*np.sin(phi[i]);

        #z[i] = r[i] * np.cos(theta[i]);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='ButterflyCurve');

    #ax.scatter(x, y, z, label='ButterflyCurve');

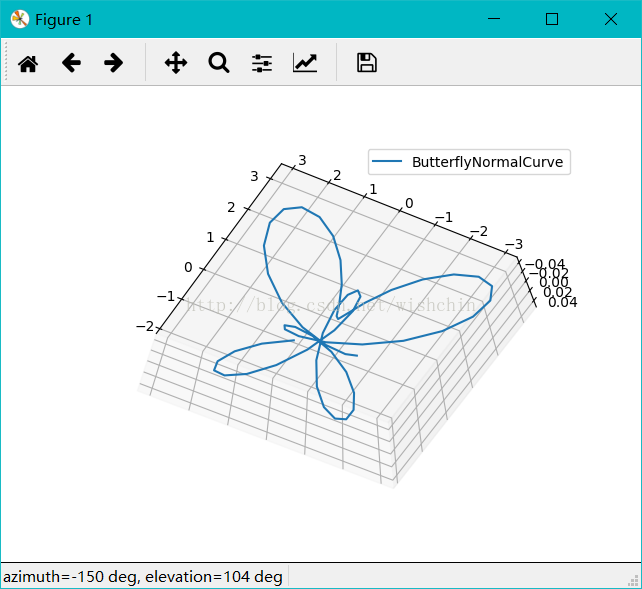
    ax.legend();

    plt.show();

def ButterflyNormalCurve():

    #蝶形曲线，使用球坐标系#或许公式是错误的，应该有更加复杂的公式

    #螺旋曲线#采用柱坐标系

    #t = np.arange(0,100,1);

    theta=np.arange(0,6,0.1);#(0,72,0.1);

    r =theta*0;

    z =theta*0;

    x =theta*0;

    y =theta*0;

    for i in range(len(theta)):

        r[i] = np.power(math.e,sin(theta[i]))- 2*cos(4*theta[i])

        + np.power( sin(1/24 * (2*theta[i] -pi ) ) , 5 );

        #x[i] = r[i] * np.sin(theta[i]);

        #y[i] = r[i] * np.cos(theta[i]);

    x = r * np.sin(theta);

    y = r * np.cos(theta);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='ButterflyNormalCurve');

    ax.legend();

    plt.show();

def phoenixCurve():

    #蝶形曲线，使用球坐标系

    t = np.arange(0,100,1);

    r = 8 * t;

    theta = 360 * t * 4 ;

    phi   = -360 * t * 8;

    x = t*1;

    y = t*1;

    z = t*1;

    for i in range(len(t)):

        x[i] = r[i] * np.sin(theta[i])*np.cos(phi[i]);

        y[i] = r[i] * np.sin(theta[i])*np.sin(phi[i]);

        z[i] = r[i] * np.cos(theta[i]);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='phoenixCurve');

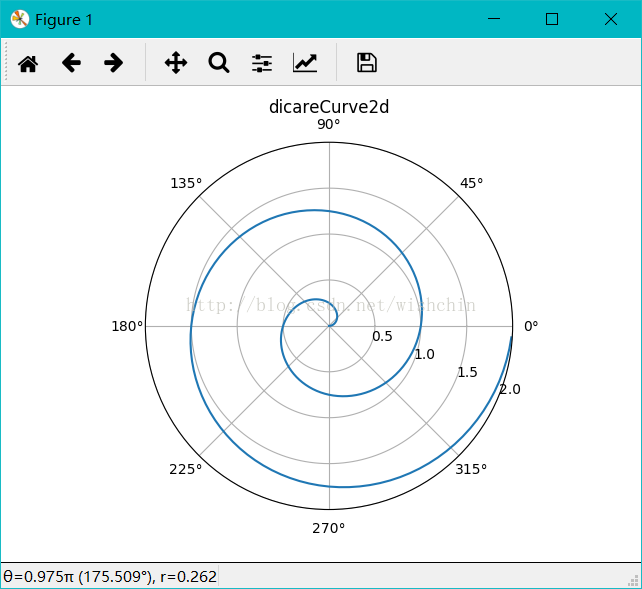
    ax.legend();

    plt.show();

def dicareCurve2d():

    r = np.arange(0, 2, 0.01)

    theta = 2 * np.pi * r

    ax = plt.subplot(111, projection='polar')

    ax.plot(theta, r)

    ax.set_rmax(2)

    ax.set_rticks([0.5, 1, 1.5, 2])  # Less radial ticks

    ax.set_rlabel_position(-22.5)  # Move radial labels away from plotted line

    ax.grid(True)

    ax.set_title("dicareCurve2d", va='bottom')

    plt.show();

def WindmillCurve3d():

    #风车曲线

    t = np.arange(0,2,0.01);

    r =t*0+1 ;

    #r=1

    ang =36*t;#ang =360*t;

    s =2*pi*r*t;

    x = t*1;

    y = t*1;

    for i in range(len(t)):

        x[i] = s[i]*cos(ang[i]) +s[i]*sin(ang[i]) ;

        y[i] = s[i]*sin(ang[i]) -s[i]*cos(ang[i]) ;

    z =t*0;

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='WindmillCurve3d');

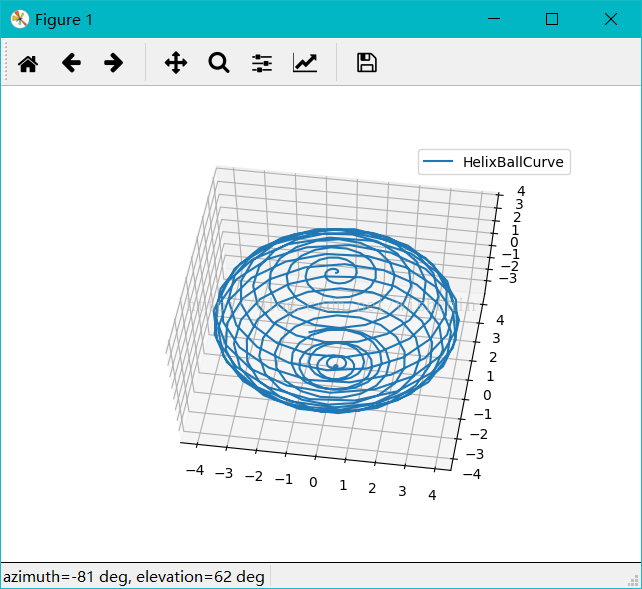
    ax.legend();

    plt.show();

def HelixBallCurve():

    #螺旋曲线，使用球坐标系

    t = np.arange(0,2,0.005);

    r =t*0+4 ;

    theta =t*1.8

    phi =t*3.6*20

    x = t*1;

    y = t*1;

    z = t*1;

    for i in range(len(t)):

        x[i] = r[i] * np.sin(theta[i])*np.cos(phi[i]);

        y[i] = r[i] * np.sin(theta[i])*np.sin(phi[i]);

        z[i] = r[i] * np.cos(theta[i]);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='HelixBallCurve');

    ax.legend();

    plt.show();

def seperialHelix():

    #螺旋曲线，使用球坐标系

    t = np.arange(0,2,0.1);

    n = np.arange(0,2,0.1);

    r =t*0+4 ;

    theta =n*1.8 ;

    phi =n*3.6*20;

    x = t*0;

    y = t*0;

    z = t*0;

    for i in range(len(t)):

        x[i] = r[i] * np.sin(theta[i])*np.cos(phi[i]);

        y[i] = r[i] * np.sin(theta[i])*np.sin(phi[i]);

        z[i] = r[i] * np.cos(theta[i]);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='ButterflyCurve');

    ax.legend();

    plt.show();

def AppleCurve():

    #螺旋曲线

    t = np.arange(0,2,0.01);

    l=2.5

    b=2.5

    x =  t*1;

    y =  t*1;

    z =0;#z=t*0;

    n = 36

    for i in range(len(t)):

        x[i]=3*b*cos(t[i]*n)+l*cos(3*t[i]*n)

        y[i]=3*b*sin(t[i]*n)+l*sin(3*t[i]*n)

    #x = r * np.sin(theta);

    #y = r * np.cos(theta);

    mpl.rcParams['legend.fontsize'] = 10;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='AppleCurve');

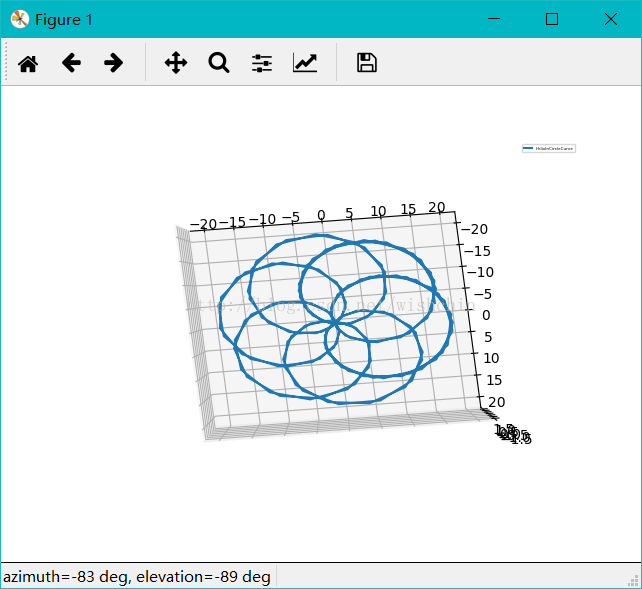
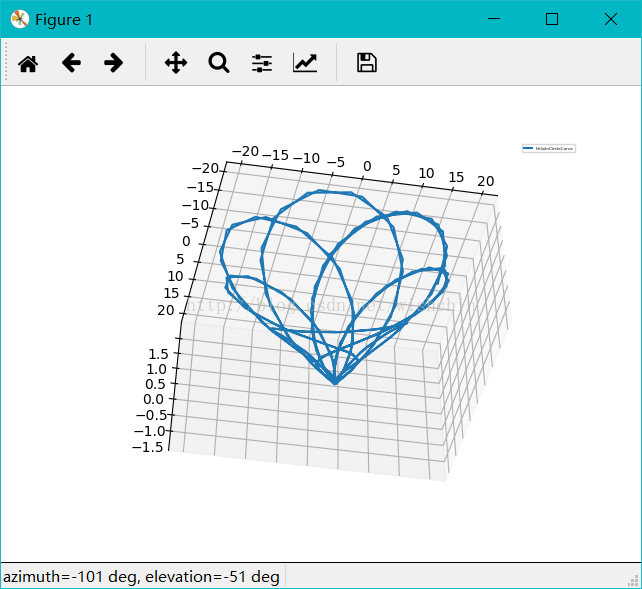
    ax.legend();

    plt.show();

def HelixInCircleCurve():

    #园内螺旋曲线#采用柱坐标系

    t = np.arange(-1,1,0.01);

    theta=t*36 ;#360 deta 0.005鸟巢网 #36 deta 0.005 圆内曲线

    x =  t*1;

    y =  t*1;

    z =  t*1;

    r =  t*1;

    n = 1.2

    for i in range(len(t)):

        r[i]=10+10*sin(n*theta[i]);

        z[i]=2*sin(n*theta[i]);

        x[i] = r[i] * np.sin(theta[i]);

        y[i] = r[i] * np.cos(theta[i]);

    mpl.rcParams['legend.fontsize'] = 3;

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.plot(x, y, z, label='HelixInCircleCurve');

    #ax.scatter(x, y, z, label='HelixInCircleCurve');

    ax.legend();

    plt.show();

def Votex3D():

    def midpoints(x):

        sl = ()

        for i in range(x.ndim):

            x = (x[sl + np.index_exp[:-1]] + x[sl + np.index_exp[1:]]) / 2.0

            sl += np.index_exp[:]

        return x

    # prepare some coordinates, and attach rgb values to each

    r, g, b = np.indices((17, 17, 17)) / 16.0

    rc = midpoints(r)

    gc = midpoints(g)

    bc = midpoints(b)

    # define a sphere about [0.5, 0.5, 0.5]

    sphere = (rc - 0.5)**2 + (gc - 0.5)**2 + (bc - 0.5)**2 < 0.5**2

    # combine the color components

    colors = np.zeros(sphere.shape + (3,))

    colors[..., 0] = rc

    colors[..., 1] = gc

    colors[..., 2] = bc

    # and plot everything

    fig = plt.figure();

    ax = fig.gca(projection='3d');

    ax.voxels(r, g, b, sphere,

              facecolors=colors,

              edgecolors=np.clip(2*colors - 0.5, 0, 1),  # brighter

              linewidth=0.5);

    ax.set(xlabel='r', ylabel='g', zlabel='b');

    plt.show();

def drawFiveFlower():

    theta=np.arange(0,2*np.pi,0.02)

    #plt.subplot(121,polar=True)

    #plt.plot(theta,2*np.ones_like(theta),lw=2)

    #plt.plot(theta,theta/6,'--',lw=2)

    #plt.subplot(122,polar=True)

    plt.subplot(111,polar=True)

    plt.plot(theta,np.cos(5*theta),'--',lw=2)

    plt.plot(theta,2*np.cos(4*theta),lw=2)

    plt.rgrids(np.arange(0.5,2,0.5),angle=45)

    plt.thetagrids([0,45,90]);

    plt.show(); 

if __name__ == '__main__':

    import argparse

    mainex();

画图结果：

  

  

   

   

    

ProE常用曲线方程：Python Matplotlib 版本代码（蝴蝶曲线）的更多相关文章

  1. ProE常用曲线方程：Python Matplotlib 版本代码（玫瑰曲线）

    Pyplot教程:https://matplotlib.org/gallery/index.html#pyplots-examples 玫瑰曲线 文字描述 平面内,围绕某一中心点平均分布整数个正弦花瓣 ...

  2. ProE复杂曲线方程：Python Matplotlib 版本代码（L系统，吸引子和分形)

    对生长自动机的研究由来已久,并在计算机科学等众多学科中,使用元胞自动机的概念,用于生长模拟.而复杂花纹的生成,则可以通过重写一定的生长规则,使用生成式来模拟自然纹理.当然,很多纹理是由人本身设计的,其 ...

  3. 常用统计分析python包开源学习代码 numpy pandas matplotlib

    常用统计分析python包开源学习代码 numpy pandas matplotlib 待办 https://github.com/zmzhouXJTU/Python-Data-Analysis

  4. python 低版本一段扫描代码

    个人在做Linux渗透测试往内网跨的时候,通常我碰到的Linux环境都会是如下集中情况 1: DMZ,严格的DMZ,根本跨不到内网里去.这种最恶心了. 2:WEB SERVER,严格区分,工作机和工作 ...

  5. python 常忘代码查询 和autohotkey补括号脚本和一些笔记和面试常见问题

    笔试一些注意点: --,23点43 今天做的京东笔试题目: 编程题目一定要先写变量取None的情况.今天就是因为没有写这个边界条件所以程序一直不对.以后要注意!!!!!!!!!!!!!!!!!!!!! ...

  6. 一文总结数据科学家常用的Python库（下）

    用于建模的Python库 我们已经到达了本文最受期待的部分 - 构建模型!这就是我们大多数人首先进入数据科学领域的原因,不是吗? 让我们通过这三个Python库探索模型构建. Scikit-learn ...

  7. 总结数据科学家常用的Python库

    概述 这篇文章中,我们挑选了24个用于数据科学的Python库. 这些库有着不同的数据科学功能,例如数据收集,数据清理,数据探索,建模等,接下来我们会分类介绍. 您觉得我们还应该包含哪些Python库 ...

  8. Python - matplotlib 数据可视化

    在许多实际问题中,经常要对给出的数据进行可视化,便于观察. 今天专门针对Python中的数据可视化模块--matplotlib这块内容系统的整理,方便查找使用. 本文来自于对<利用python进 ...

  9. 我常用的 Python 调试工具 - 博客 - 伯乐在线

    .ckrating_highly_rated {background-color:#FFFFCC !important;} .ckrating_poorly_rated {opacity:0.6;fi ...

随机推荐

  1. NOIP2010 提高组合集

    NOIP 2010 提高组合集 T1 机器翻译 模拟题,用一个栈模拟,桶记录即可. #include <iostream> #include <cstdio> #include ...

  2. log4j.properties的简单配置和使用

    log4j.properties  // 日志文件名不能随便写, 是properties文件 log4j.rootLogger=INFO, Console //表示INFO级别 输出到控制台 #Con ...

  3. MyBatis3错误：Exception in thread "main" java.lang.NoClassDefFoundError: org/apache/log4j/Priority的问题解决

    在使用Maven新建QuitStart类型项目时,引入了MyBatis3.2.0版本的JAR包之后,出现如下错误: Exception in thread "main" java. ...

  4. 非常适合新手的jq/zepto源码分析05

    zepto的原型  $.fn  属性: constructor //构造行数 forEach: emptyArray.forEach, //都是原生数组的函数reduce: emptyArray.re ...

  5. LeetCode 234. Palindrome Linked List （回文链表）

    Given a singly linked list, determine if it is a palindrome. Follow up:Could you do it in O(n) time ...

  6. vim入门级使用

    1.刚进入是 command mode 命令行模式 2.i  进入插入 insert  mode 模式 在插入模式下只能 输入内容,如果要删除内容,需要切换到命令行模式,移动光标进行删除. 3.esc ...

  7. linux下查看一个文件的属性（ls，lsattr，file，stat）

    查看文件属性有多种方法,且这些方法中偏向不同,具体如下:1,ls    ls -a 查看所有文件    ls -l 查看详细的属性  2,lsattr    查看文件的扩展属性,    如果文件被 c ...

  8. 启动Tomcat任何程序都报错

    启动Tomcat出现: Cannot publish to the server because it is missing its runtime environment. 可能是servers中不 ...

  9. 【POJ 2503】 Babelfish

    [题目链接] http://poj.org/problem?id=2503 [算法] 字符串哈希 [代码] #include <algorithm> #include <bitset ...

  10. 设计模式（二）：单例模式（DCL及解决办法）

    public class Singleton { //懒汉模式 双重检查锁定DCL(double-checked locking) //缺点:由于jvm存在乱序执行功能,DCL也会出现线程不安全的情况 ...