开店 BZOJ 4012

开店

【问题描述】

风见幽香有一个好朋友叫八云紫，她们经常一起看星星看月亮从诗词歌赋谈到人生哲学。最近她们灵机一动，打算在幻想乡开一家小店来做生意赚点钱。这样的想法当然非常好啦，但是她们也发现她们面临着一个问题，那就是店开在哪里，面向什么样的人群。很神奇的是，幻想乡的地图是一个树形结构，幻想乡一共有 n个地方，编号为 1 到 n，被 n-1 条带权的边连接起来。每个地方都住着一个妖怪，其中第 i 个地方的妖怪年龄是 x_i。妖怪都是些比较喜欢安静的家伙，所以它们并不希望和很多妖怪相邻。所以这个树所有顶点的度数都小于或等于 3。妖怪和人一样，兴趣点随着年龄的变化自然就会变化，比如我们的 18 岁少女幽香和八云紫就比较喜欢可爱的东西。幽香通过研究发现，基本上妖怪的兴趣只跟年龄有关，所以幽香打算选择一个地方 u（u为编号），然后在 u开一家面向年龄在 L到R 之间（即年龄大于等于 L、小于等于 R）的妖怪的店。也有可能 u这个地方离这些妖怪比较远，于是幽香就想要知道所有年龄在 L 到 R 之间的妖怪，到点 u 的距离的和是多少（妖怪到 u 的距离是该妖怪所在地方到 u 的路径上的边的权之和） ，幽香把这个称为这个开店方案的方便值。幽香她们还没有决定要把店开在哪里，八云紫倒是准备了很多方案，于是幽香想要知道，对于每个方案，方便值是多少呢。

【输入格式】

第一行三个用空格分开的数 n、Q和A，表示树的大小、开店的方案个数和妖怪的年龄上限。

第二行n个用空格分开的数 x_1、x_2、…、x_n，x_i 表示第i 个地点妖怪的年龄，满足0<=x_i<A。(年龄是可以为 0的，例如刚出生的妖怪的年龄为 0。)

接下来 n-1 行，每行三个用空格分开的数 a、b、c，表示树上的顶点 a 和 b 之间有一条权为c(1 <= c <= 1000)的边，a和b 是顶点编号。

接下来Q行，每行三个用空格分开的数 u、 a、 b。对于这 Q行的每一行，用 a、b、A计算出 L和R，表示询问“在地方 u开店，面向妖怪的年龄区间为[L,R]的方案的方便值是多少”。

对于其中第 1 行，L 和 R 的计算方法为：L=min(a%A,b%A), R=max(a%A,b%A)。

对于第 2 到第 Q 行，假设前一行得到的方便值为 ans，那么当前行的 L 和 R 计算方法为： L=min((a+ans)%A,(b+ans)%A), R=max((a+ans)%A,(b+ans)%A)。

【输出格式】

对于每个方案，输出一行表示方便值。

【样例输入】

10 10 10

0 0 7 2 1 4 7 7 7 9

1 2 270

2 3 217

1 4 326

2 5 361

4 6 116

3 7 38

1 8 800

6 9 210

7 10 278

8 9 8

2 8 0

9 3 1

8 0 8

4 2 7

9 7 3

4 7 0

2 2 7

3 2 1

2 3 4

【样例输出】

1603

957

7161

9466

3232

5223

1879

1669

1282

0

【数据范围】

满足 n<=150000,Q<=200000。对于所有数据，满足 A<=10^9

---

题解：

画图分析可知：

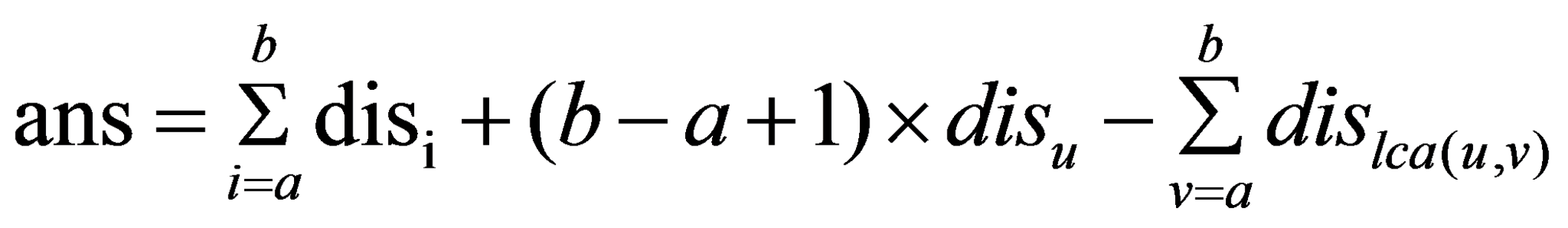
其中dis表示点到根的距离，区间[a,b]表示在要求年龄范围内的点，lca(u,v)表示点u和点v的最近公共祖先

点u的所有祖先都在根到u的路径上，点v同样

那么树链剖分+可持久化线段树

以dfs序建立线段树

将每个点按年龄顺序加入

在树剖往上跳的过程中，覆盖祖先到它的区间，表示有一个点经过这些点

用前缀和处理出这一段区间的边权和（边为它父亲连向它的边），就可以区间加了

查询时第一部分也也用前缀和维护，第二部分直接求，第三部分用可持久化线段树

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 typedef long long lol;
 inline int Get()
 {
     int x;
     char c;
     while((c = getchar()) < '' || c > '');
     x = c - '';
     while((c = getchar()) >= '' && c <= '') x = x *  + c - '';
     return x;
 }
 const int me = ;
 const int inf = ;
 struct point
 {
     int id, age;
 };
 point dot[me];
 inline bool operator < (const point &a, const point &b)
 {
     if(a.age != b.age) return a.age < b.age;
     return a.id < b.id;
 }
 int n, q;
 int root;
 int rt[me];
 int tot, to[me], fir[me], nex[me];
 lol mo;
 lol val[me];
 inline void Ins(const int &x, const int &y, const int &z)
 {
     nex[++tot] = fir[x];
     fir[x] = tot;
     to[tot] = y;
     val[tot] = z;
 }
 int stamp;
 int si[me], pos[me], top[me], son[me], fat[me], last[me];
 lol dis[me];
 void Chain_one(const int &u)
 {
     si[u] = ;
     for(int i = fir[u]; i; i = nex[i])
     {
         int v = to[i];
         if(v == fat[u]) continue;
         fat[v] = u;
         last[v] = val[i];
         dis[v] = dis[u] + val[i];
         Chain_one(v);
         si[u] += si[v];
         if(si[son[u]] < si[v]) son[u] = v;
     }
 }
 lol sum_dis[me], sum_edge[me];
 void Chain_two(const int &u)
 {
     pos[u] = ++stamp;
     sum_edge[stamp] = last[u];
     if(son[u])
     {
         top[son[u]] = top[u];
         Chain_two(son[u]);
     }
     for(int i = fir[u]; i; i = nex[i])
     {
         int v = to[i];
         if(v == son[u] || v == fat[u]) continue;
         top[v] = v;
         Chain_two(v);
     }
 }
 int lc[], rc[];
 lol sum[], cnt[];
 int Modify(const int &y, const int &l, const int &r, const int &a, const int &b)
 {
     int x = ++tot;
     lc[x] = lc[y];
     rc[x] = rc[y];
     sum[x] = sum[y];
     cnt[x] = cnt[y];
     if(a == l && b == r)
     {
         ++cnt[x];
         return x;
     }
     sum[x] += sum_edge[b] - sum_edge[a - ];
     int mi = l + r >> ;
     if(a > mi) rc[x] = Modify(rc[x], mi + , r, a, b);
     else
         if(b <= mi) lc[x] = Modify(lc[x], l, mi, a, b);
         else
             lc[x] = Modify(lc[x], l, mi, a, mi), rc[x] = Modify(rc[x], mi + , r, mi + , b);
     return x;
 }
 lol Query(const int &x, const int &l, const int &r, const int &a, const int &b)
 {
     lol res = (sum_edge[b] - sum_edge[a - ]) * cnt[x];
     if(a == l && b == r) return res + sum[x];
     int mi = l + r >> ;
     if(a > mi) return res + Query(rc[x], mi + , r, a, b);
     if(b <= mi) return res + Query(lc[x], l, mi, a, b);
     return res + Query(lc[x], l, mi, a, mi) + Query(rc[x], mi + , r, mi + , b);
 }
 inline int Add(int x)
 {
     while(top[x] != )
     {
         root = Modify(root, , n, pos[top[x]], pos[x]);
         x = fat[top[x]];
     }
     root = Modify(root, , n, pos[top[x]], pos[x]);
     return root;
 }
 inline lol Ask(const int &rt, int x)
 {
     lol res = ;
     while(top[x] != )
     {
         res += Query(rt, , n, pos[top[x]], pos[x]);
         x = fat[top[x]];
     }
     return res + Query(rt, , n, pos[top[x]], pos[x]);
 }
 int main()
 {
     n = Get(), q = Get(), mo = Get();
     for(int i = ; i <= n; ++i) dot[i] = (point) {i, Get()};
     sort(dot + , dot +  + n);
     for(int i = ; i < n; ++i)
     {
         int x, y, z;
         x = Get(), y = Get(), z = Get();
         Ins(x, y, z);
         Ins(y, x, z);
     }
     Chain_one();
     top[] = ;
     Chain_two();
     for(int i = ; i <= n; ++i)
     {
         sum_edge[i] += sum_edge[i - ];
         sum_dis[i] = sum_dis[i - ] + dis[dot[i].id];
     }
     tot = ;
     for(int i = ; i <= n; ++i) rt[i] = Add(dot[i].id);
     lol ans = ;
     while(q--)
     {
         lol u = Get(), a = Get(), b = Get();
         a = (a + ans) % mo;
         b = (b + ans) % mo;
         if(a > b) swap(a, b);
         a = lower_bound(dot + , dot +  + n, (point) {, a}) - dot;
         b = upper_bound(dot + , dot +  + n, (point) {inf, b}) - dot - ;
         lol c, d;
         c = Ask(rt[a - ], u);
         d = Ask(rt[b], u);
         ans = sum_dis[b] - sum_dis[a - ] + (b - a + ) * dis[u] - ((d - c) << );
         printf("%lld\n", ans);
     }
 }