Codeforces Round #329 (Div. 2) D. Happy Tree Party(LCA+并查集)

题目链接

题意:就是给你一颗这样的树，用一个$y$来除以两点之间每条边的权值，比如$3->7$，问最后的y的是多少，修改操作是把权值变成更小的。

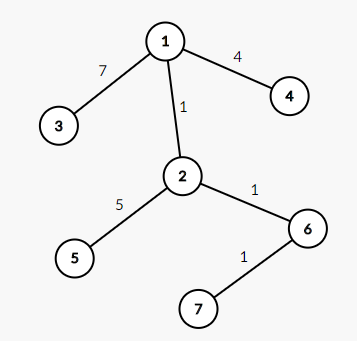
这个$(y<=10^{18})$除的权值如果是$>=2$，那么最多除60几次就变成0了，问题关键是路径上会有好多1存在，这时候我们可以用并查集把他们并到一块，这样就能跳着查了。

具体查法：

从$u$到$LCA(u,v)$，路径上除一遍。

从$v$到$LCA(u,v)$，路径上除一遍。

修改操作如果变成1，就与前面的点合并。

 #include <iostream>
 #include <algorithm>
 #include <cstdio>
 using namespace std;

 typedef long long ll;
 const int maxn = 2e5 + ;
 ///加边
 int cnt = , h[maxn];
 struct edge
 {
     int to, pre;
     ll v;
 } e[maxn << ];
 void add(int from, int to, ll v)
 {
     cnt++;
     e[cnt].pre = h[from]; ///5-->3-->1-->0
     e[cnt].to = to;
     e[cnt].v = v;
     h[from] = cnt;
 }
 ///LCA
 int dist[maxn];
 int dep[maxn];
 int anc[maxn][]; ///2分的父亲节点
 ll len[maxn];
 void dfs(int u, int fa)
 {
     for(int i = h[u]; i; i = e[i].pre)
     {
         int v = e[i].to;
         if(v == fa) continue;
         dist[v] = dist[u] + e[i].v;
         dep[v] = dep[u] + ;
         anc[v][] = u;
         len[v] = e[i].v;
         dfs(v, u);
     }
 }
 void LCA_init(int n)
 {
     for(int j = ; ( << j) < n; j++)
         for(int i = ; i <= n; i++) if(anc[i][j-])
         anc[i][j] = anc[anc[i][j-]][j-];
 }
 int LCA(int u, int v)
 {
     int log;
     if(dep[u] < dep[v]) swap(u, v);
     for(log = ; ( << log) < dep[u]; log++);
     for(int i = log; i >= ; i--)
         if(dep[u] - ( << i) >= dep[v]) u = anc[u][i];
     if(u == v) return u;
     for(int i = log; i >= ; i--)
         if(anc[u][i] && anc[u][i] != anc[v][i])
             u = anc[u][i], v = anc[v][i];
     return anc[u][];
 }
 int fa[maxn];
 int Find(int x)
 {
     if(x == fa[x]) return x;
     return fa[x] = Find(fa[x]);
 }
 int main()
 {
     int n, m; scanf("%d %d", &n, &m);
     cnt = ;
     for(int i = ; i <= n; i++) h[i] = ;
     for(int i = ; i <= n - ; i++)
     {
         int u, v;
         ll w; scanf("%d %d %lld", &u, &v, &w);
         add(u, v, w), add(v, u, w);
     }
     ///LCA初始化
     dfs(, );
     LCA_init(n);
     ///并查集初始化
     for(int i = ; i <= n; i++) fa[i] = i;
     while(m--)
     {
         int op, a, b, p;
         ll c, y;
         scanf("%d", &op);
         if(op == )
         {
            scanf("%d %d %lld", &a, &b, &y);
            int fp = LCA(a, b);
            a = Find(a);
            while(dep[a] > dep[fp] && y > 0LL)
            {
                if(len[a] == 1LL)
                {
                    fa[a] = anc[a][];
                    a = Find(a);
                }
                else
                {
                    y /= len[a];
                    a = Find(anc[a][]);
                }
            }
            b = Find(b);
            while(dep[b] > dep[fp] && y > 0LL)
            {
                if(len[b] == 1LL)
                {
                    fa[b] = anc[b][];
                    b = Find(b);
                }
                else
                {
                    y /= len[b];
                    b = Find(anc[b][]);
                }
            }
            printf("%lld\n", y);
         }
         else
         {
             scanf("%d %lld", &p, &c);
             int u = e[p * ].to, v = e[(p * ) ^ ].to;
             if(u == anc[v][])
             {
                 len[v] = c;
                 if(c == 1LL)
                 {
                     fa[v] = u;
                 }
             }
             else
             {
                 len[u] = c;
                 if(c == 1LL)
                 {
                     fa[u] = v;
                 }
             }
         }
     }
     return ;
 }