Unity插值函数Lerp()与增量时间Time.deltatime

一、Unity插值函数Lerp()

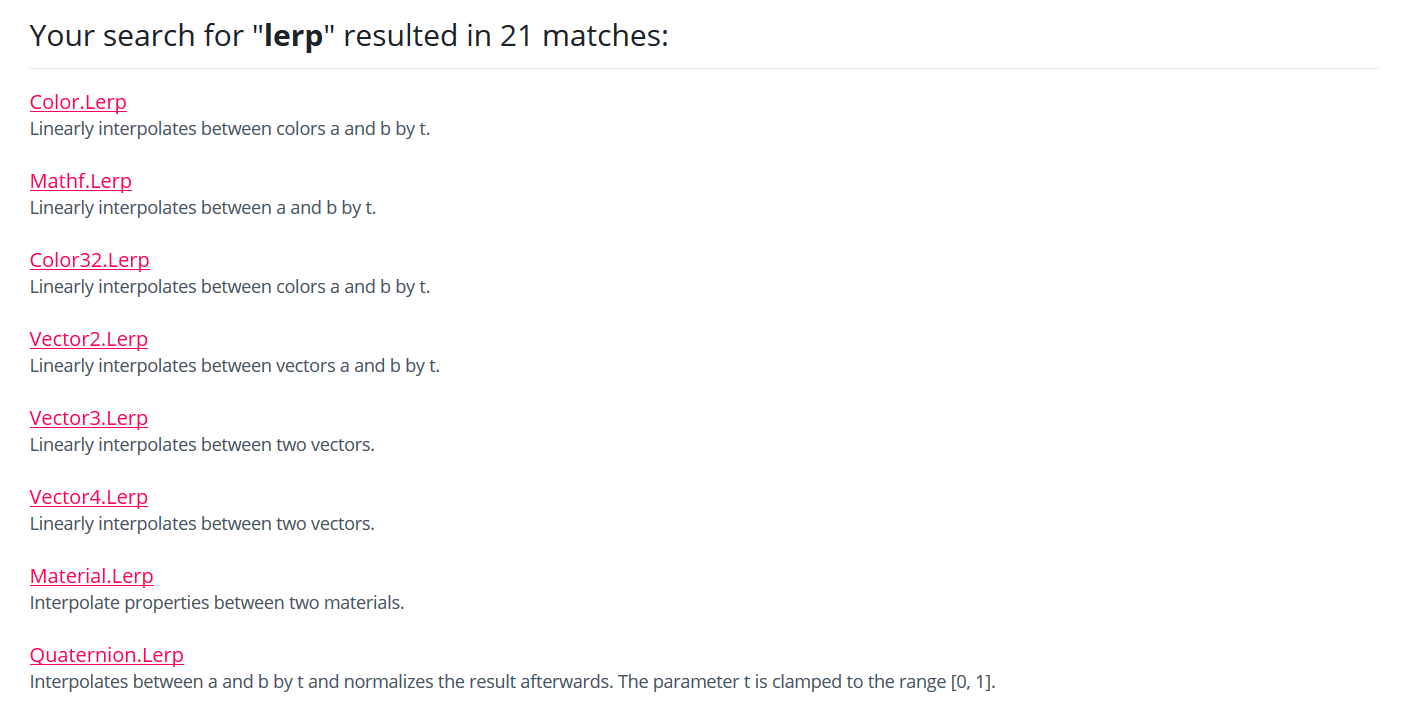
通过官方文档简单了解插值函数(https://docs.unity3d.com/ScriptReference/index.html)，可以看到插值函数有很多

Mathf.Lerp()

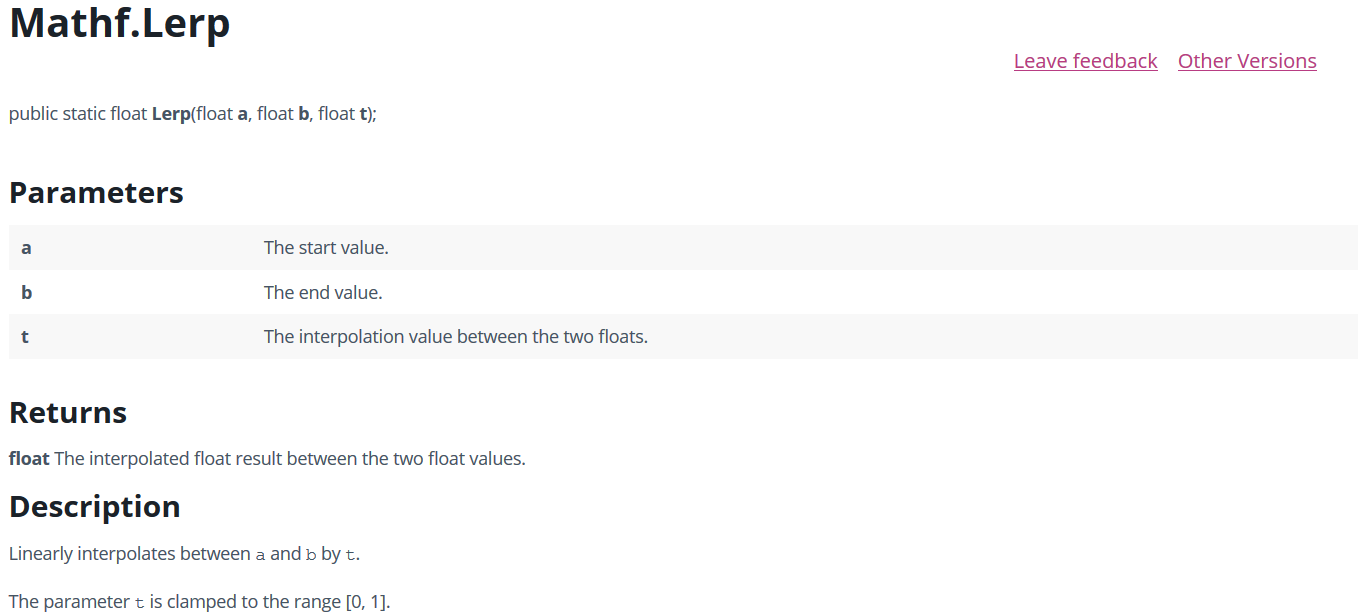
从最简单的数学插值来看，插值函数接收三个参数a，b，t，在ab之间，以t作为比例来插值。

例如，Lerp(0, 10, 0.4f)，此时返回4，即 a + (b - a) * t

注意，第三个参数要小于1，如果大于1，则还是返回b。

其他的插值也类似于此，只不过插值的对象变为向量，颜色等等。

二、增量时间Time.deltatime

游戏都是一帧一帧显示的，平时说的60FPS就是1秒60帧；帧率越高，游戏运行就越流畅。

增量时间deltatime，就是从上一帧到现在所经过的时间。如果游戏稳定在60FPS，那么增量时间就是1/60s，当然实际游戏运行帧数肯定在不断变化，所以Time.delta的值也在不断地变化。简单来说，Time.deltatime就是运行每一帧所花的时间。

三、插值函数的作用

在看官方文档以及其他的代码时，经常发现插值函数的第三个参数往往和增量时间有关，如：

using UnityEngine;

public class Example : MonoBehaviour
{
    Transform target;
    float speed = 0.1f;
    void Update()
    {
        transform.position = Vector3.Lerp(transform.positon, target.position, Time.deltatime * speed);
    }
}

那么为什么线性插值的第三个参数要用到增量时间呢？

首先，需要理解为什么要利用插值函数。

不妨想象以下游戏场景，在主人身后有一只宠物，它会时刻跟在主人身后，如果主人走远了，它也会快速跟上。

可以发现两点，第一，宠物不是瞬间移动到主人身后的，而是一点一点走过来的，第二，宠物和主人离得越远，宠物跟随的速度就越快，离主人越近，宠物的速度就越慢，而Lerp()函数就可以实现弹性跟随的效果。

transform.position = Vector3.Lerp(transform.positon, target.position, Time.deltatime * speed);

这行代码中，Lerp()函数返回一个自身位置和target位置之间的一个位置，比例是Time.deltatime * speed，然后再把这个值作为自己的新位置

如果第三个参数是0.5，自身位置为0，目标位置为10，那么第一次自身从0移动到5，第二次从5移动到7.5，即每次都会移动（目标位置 - 自身位置）* 0.5的位置，由于自己越来越接近目标位置，这个值也会越来越小，所以每次往前移动的距离也就越来越小，这样就实现了弹性的效果。

当然，从数学的角度来看，只能无限接近目标位置，永远也到达不了目标位置，但是玩家是感觉不出这一点的差距的。

四、使用增量时间进行插值

最后回到本篇的重点，为什么在插值函数中要使用增量时间作为参数呢？

还是以最简单的数学插值为例

a = Mathf.Lerp(a, b, 0.1f);

每次运行后，a都会以10%的速度向b靠近。假设a和b之间相差1个单位，第一帧后，a和b之间剩余的距离变为0.9，第二帧过后，a和b之间剩余的距离变为0.81 = 0.9 * 0.9。以此类推，第n帧过后，a和b之间的剩余距离变为0.9^n

如果FPS=10，那么一秒后a和b之间的剩余距离变为0.9^10，如果如果FPS=20，那么一秒后a和b之间的剩余距离变为0.9^20，也就是说插值效果和电脑运行的帧率有关。

下面考虑使用增量时间的情况（一般会用speed来乘以增量时间，这里为了简化就假设speed为1）

a = Mathf.Lerp(a, b, Time.deltatime);

类似的，在n帧过后，a和b之间的剩余距离变为 (1 - Time.deltatime) ^ n，如果假设电脑帧率稳定的话，根据增量时间的定义，Time.deltatime表示每帧运行的事件，即Time.deltatime= 1/n

那么，a和b之间的剩余距离变为 (1 - 1/n) ^ n。可以看出，插值效果仍然和帧率有关，但是如果带入数字详细计算的话，会发现实际差距已经很小。

例如，n = 30，即FPS=30，那么结果大致是0.36166，如果 n = 60，结果大致是0.36479

这种写法比较简便，而且不同帧率下的插值效果相差很小，这也是为什么大部分代码都会这么写的原因。

最后，给出如下写法：

a = Mathf.Lerp(a, b, 1 - speed ^ Time.deltatime);

通过同样的计算可得，a和b之间的剩余距离变为 [1 - (1 - speed ^ (1/n) ] ^ n = speed，这种写法做到了完全和帧率无关，即无论在哪一台电脑上运行，在相同的时间后都会有相同的插值效果

五、总结

在不苛求完美的情况下，一般采取第二种写法，就可以取得较好的插值效果效果

参考文章：https://www.construct.net/en/blogs/ashleys-blog-2/using-lerp-delta-time-924