BZOJ2038 [2009国家集训队]小Z的袜子 莫队+分块

作为一个生活散漫的人，小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿。终于有一天，小Z再也无法忍受这恼人的找袜子过程，于是他决定听天由命……

具体来说，小Z把这N只袜子从1到N编号，然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双，

甚至不在意两只袜子是否一左一右，他却很在意袜子的颜色，毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z，他有多大的概率抽到两只颜色相同的袜子。当然，小Z希望这个概率尽量高，所以他可能会询问多个(L,R)以方便自己选择

题解:

　　先推公式:

　　对于一个区间$[l,r]$,每种袜子的个数$c_i$,其拿到一对相同袜子的种类数等于:

　　　　　　

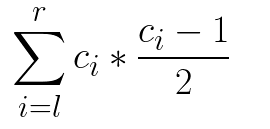
　　总的种类则为:

　　　　　　

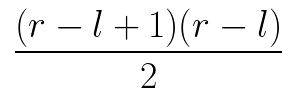
　　所以最终的概率就是:

　　　　　　

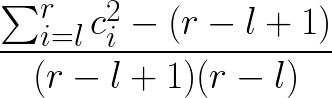
　　　　(博客园的latex老出bug,脑壳痛)

　　显然,问题是如何求分子,也就是一个区间内,每种数字个数的的平方和

　　首先想到线段树,但是这个题显然不满足区间加法,普通的线段树无法解决

　　即,无法通过$[l,m]$与$[m+1,r]$的答案,直接得到$[l,r]$的答案

　　于是考虑采用莫队算法离线询问,因为我们发现,一旦我们得到了$[l,r]$的答案

　　我们就可以$O(1)$的得到$[l\pm 1,r]$与$[l,r\pm 1]$的答案,我们按区间排序询问即可

　　那如何最少次数的转移来得到所有答案呢?

　　问题就等价于平面上的曼哈顿最小生成树了

　　曼哈顿最小生成树的算法是$O(nlogn)$的

　　但在这道题上,根据证明,复杂度会退化

　　于是考虑使用数列分块,每次移动区间的时候,按照块移动

　　我们记录当前的询问的$l$和$r$

　　询问按照$l$所属的块进行排序,同一块内按照$r$排序

　　

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=1e5+10;
const int INF=0x3f3f3f3f;
int casn,n,m,k,size;
ll num[maxn],sum[maxn],ans1[maxn],ans2[maxn];
int id[maxn];
struct node{
	int l,r,id;
}cmd[maxn];
int cmp(node a,node b){
	if(id[a.l]==id[b.l]) return a.r<b.r;
	return id[a.l]<id[b.l];
}
void update(ll &now,int pos,int x) {
	now-=sum[num[pos]]*sum[num[pos]];
	sum[num[pos]]+=x;
	now+=sum[num[pos]]*sum[num[pos]];
}
int main() {
	scanf("%d%d",&n,&m);
	size=sqrt(n);
	for(int i=1;i<=n;i++) id[i]=(i-1)/size+1;
	for(int i=1;i<=n;i++) scanf("%lld",num+i);
	int a,b;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&a,&b);
		cmd[i]=(node){a,b,i};
	}
	ll now=0,gcd,c,d;
	int l=1,r=0;
	sort(cmd+1,cmd+1+m,cmp);
	for(int i=1;i<=m;i++){
		while(l<cmd[i].l)update(now,l++,-1);
		while(r>cmd[i].r)update(now,r--,-1);
		while(l>cmd[i].l)update(now,--l,1);
		while(r<cmd[i].r)update(now,++r,1);
		if(cmd[i].l==cmd[i].r){
			ans2[cmd[i].id]=1;
			continue;
		}
		c=now-(cmd[i].r-cmd[i].l+1);
		d=(ll)(cmd[i].r-cmd[i].l)*(cmd[i].r-cmd[i].l+1);
		gcd=__gcd(c,d);
		ans1[cmd[i].id]=c/gcd;
		ans2[cmd[i].id]=d/gcd;
	}
	for(int i=1;i<=m;i++) {
		printf("%lld/%lld\n",ans1[i],ans2[i]);
	}
	return 0;
}

　　没有用读入优化,开了之后应该是不到1000ms