Dijkstra—校园景点游览问题
#include<iostream>
#include<cstdio>
#include<cstring>
#define MAX 9999999
using namespace std;
typedef struct ArcCell{
int length;//两点间的距离
}ArcCell, AdjMatrix[][];
//景点
typedef struct {
char sce_name[];//景点名称
int sce_num;//景点代号
char sce_intro[];//景点简介
}Scenery;
//图的数组表示法
typedef struct {
Scenery vexs[];
AdjMatrix arcs;
int vexnum,arcnum;
}MGraph;
//全局变量
int Path[];//记录最短路径上的节点
int D[];//记录节点到起始节点的距离
bool final[];//标记该节点是否在路径上
//由风景名称获取风景在数组中的下标
int GetSce(char sce_name[],MGraph G){
int i;
for(i=;i<=G.vexnum;i++)
if(strcmp(sce_name,G.vexs[i].sce_name)==)return i;
return -;
}
//创建一个图
void Creat_Graph(MGraph &G){
int i,j;
int n1,n2,weight; //起始下标、终止下标、权值
char start[], end[];
printf("■请输入景点个数: ");
scanf("%d",&G.vexnum);//景点个数
printf("■请输入路的条数: ");
scanf("%d",&G.arcnum);//路的条数
printf("\n■输入景点信息(名称(char)、代号(int)、简介(char)). \n");
for(i=;i<=G.vexnum;i++){
printf("第 %d 个景点: ",i);
scanf("%s",G.vexs[i].sce_name);
scanf("%d",&G.vexs[i].sce_num);
scanf("%s",G.vexs[i].sce_intro);
}
printf("\n■输入路况: \n");
//先把二维数组给填一下 (相当于vexnum阶矩阵)
for(i=;i<=G.vexnum;i++){
for(j=;j<=G.vexnum;j++){
G.arcs[i][j].length = MAX;
}
} for(i=;i<=G.arcnum;i++){
printf("■弧头 & 弧尾 & 权值: ");
scanf("%s",start);
scanf("%s",end);
n1 = GetSce(start,G);//经上面的景点信息获取景点的下标
n2 = GetSce(end,G);
scanf("%d",&weight);
G.arcs[n1][n2].length = weight;//矩阵双向的权值
G.arcs[n2][n1].length = weight;
}
printf("OK! 信息录入完毕!\n\n");
}
//输出最短路径
void OutPutPath(MGraph G,bool find,int sn,int en){
int i;
int path[];
if(!find){
printf("Sorry,无法找到从%s到%s的路.\n\n",G.vexs[sn].sce_name,G.vexs[en].sce_name);
return;
}
else {
printf("\n■■■%s 到 %s 最短路径上依次为: ",G.vexs[sn].sce_name,G.vexs[en].sce_name);
path[] = en;
int k = ,x = Path[en];
while(x != sn){
path[k++] = x;
x = Path[x];
}
path[k] = sn;
for(i=k;i>=;i--){
printf("%s",G.vexs[path[i]].sce_name);
if(i!=){
printf(" → ");
}
}
printf("\n■■■其最短路径长度为: %d\n",D[en]);
printf("\n");
}
}
//迪杰斯特拉算法求最短路径
void Dijkstra(MGraph G,int sn,int en){
int i;
int v, min;//v--点的下标,min--节点离起始的距离
for(i=; i<=G.vexnum; i++){
final[i] = false;//用于记录是否在已确定的点的集合中
D[i] = G.arcs[sn][i].length;//每个点与起点的距离
//初始化记录最短路径的数组
if(D[i]!= MAX)//与起点相连
Path[i] = sn;
else//不与起点相连
Path[i] = ;
}
D[sn] = ;//初始化最开始的距离0
final[sn] = true;//起始节点在路径上
Path[sn] = sn;//记录最短路径上的第一个节点
bool find = false;//判断是否找到从起点到终点的路
while(){
min = MAX;
v = -;//先默认一个不存在的下标,下面根据各步的比较把最近点的下标赋给v
for(i = ; i <= G.vexnum; i++){//找到当前位置与起点最近的点
if(final[i]==false && D[i] < min){//剩下的Ian还没连到最短路径上,而且点和最短路径的节点有通路
v = i;
min = D[i];
}
}
if(v==-){//如果找不到最近的点,就没有必要求最短路径了,直接输出找不到路
find = false;
break;
}
final[v] = true;
for(i=;i<=G.vexnum;i++){//修改每个点到起点的最近距离 ,若修改了,则说明通过v点修改点离起点更近了,此时记录Path[i] = v;
if(final[i]==false && (min + G.arcs[v][i].length <D[i])){
D[i] = min + G.arcs[v][i].length;
Path[i] = v;//这样就把下一个最近的点连接到路径上了
}
}
if(v == en){//到达尾节点,结束循环
find = true;
break;
}
}
OutPutPath(G,find,sn,en);//输出最短路径
}
int main(){
while(){
MGraph G;
char start[],end[],name[],num;//起点集、终点集、名称集、景点对应的下标
int sn,en,choice;//起始点、终止点
printf("\t\t■校园景点游览■\n");
Creat_Graph(G);//创建图
while(){
printf("■用户操作:\n");
printf("(1)景点信息 (2)最短距离\n");
scanf("%d",&choice);
if(choice == ){
printf("■请输入要查找的景点的名称: ");
scanf("%s",name);
num = GetSce(name, G);
printf("名称:%s 代号:%d 简介:%s\n\n",name,G.vexs[num].sce_num,G.vexs[num].sce_intro);
}else if(choice == ){
printf("起点 & 终点:");
scanf("%s",start);
scanf("%s",end);
sn = GetSce(start,G);
en = GetSce(end,G);
if(sn==en)
printf("您输入的起始位置和终止位置相等,所以不必查询.\n\n");
else
Dijkstra(G,sn,en);//输出最短路径
}
printf("■请输入您的选择:\n");
printf("■(0)继续查询 (1)退出 \n\n");
int q;
scanf("%d",&q);
if(q){
printf("May the code be with u!");
exit();
}
}
}
return ;
}
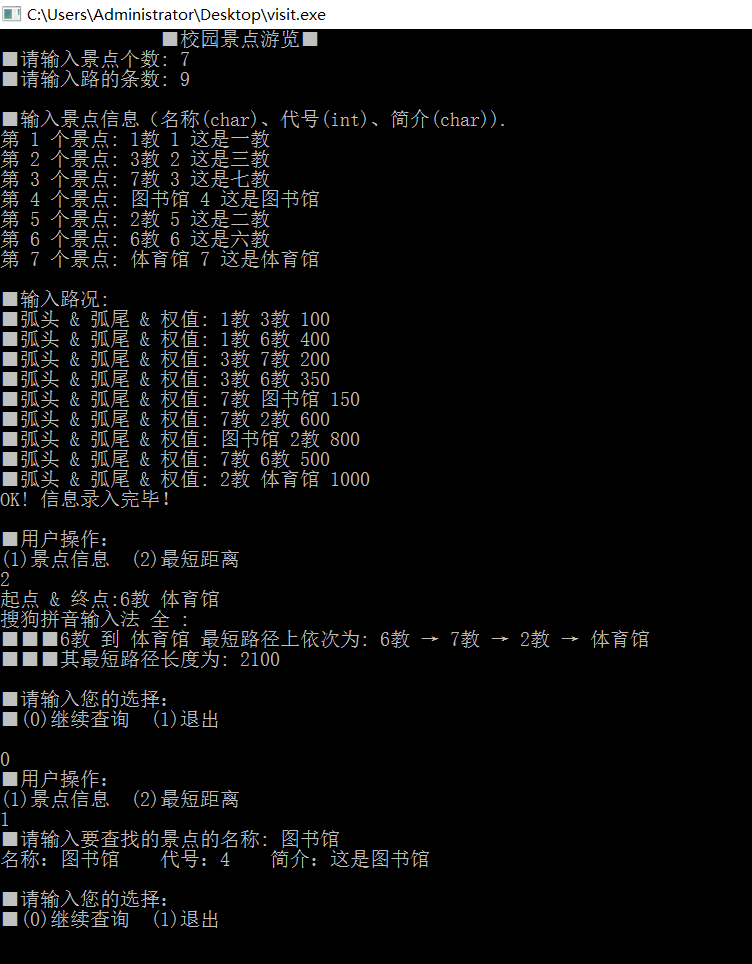
Dijkstra—校园景点游览问题的更多相关文章
- Java实现 蓝桥杯 算法训练 景点游览
试题 算法训练 景点游览 资源限制 时间限制:1.0s 内存限制:256.0MB 问题描述 小明来到一个景区游玩,但是他的时间有限,没办法逛遍所有的景点,所以他从网上下载了每个景点的评分,他希望能够使 ...
- 每日Scrum--No.9
Yesterday:测试软件 Today:写阶段性的总结 Problem: (1)晚上我们的团队进行了收尾工作:第一阶段的任务基本完成,软件主要实现了校园景点照片以及对应的介绍,查询最短路径,查询涉及 ...
- hiho 第118周 网络流四·最小路径覆盖
描述 国庆期间正是旅游和游玩的高峰期. 小Hi和小Ho的学习小组为了研究课题,决定趁此机会派出若干个调查团去沿途查看一下H市内各个景点的游客情况. H市一共有N个旅游景点(编号1..N),由M条单向游 ...
- A*寻路算法的探寻与改良(三)
A*寻路算法的探寻与改良(三) by:田宇轩 第三分:这部分内容基于树.查找算法等对A*算法的执行效率进行了改良,想了解细 ...
- A*寻路算法的探寻与改良(二)
A*寻路算法的探寻与改良(二) by:田宇轩 第二部分:这部分内容主要是使用C语言编程实现A*, ...
- poj 3229 The Best Travel Design ( 图论+状态压缩 )
The Best Travel Design Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 1359 Accepted: ...
- 各团队对《t铁大导航》评价及我组回复
组名 对我们组的建议 我组回复 (1)跑男 你们的导航前期要做到什么样的程度呢?其实我一直是很期待你们完成时我能够用你们的导航来感受一下咱们铁大校园风情.你们用了数据结构算法来找最短路径,那你们能不能 ...
- 【每日scrum】NO.9
(1)这是我们冲刺的最后一天,晚上我们的团队进行了收尾工作:第一阶段的任务基本完成,软件主要实现了校园景点照片以及对应的介绍,查询最短路径,查询涉及相关景点的查询,查询全部路径,基本界面的设计,导航功 ...
- hihocoder #1394 : 网络流四·最小路径覆盖(最小路径覆盖)
#1394 : 网络流四·最小路径覆盖 时间限制:10000ms 单点时限:1000ms 内存限制:256MB 描述 国庆期间正是旅游和游玩的高峰期. 小Hi和小Ho的学习小组为了研究课题,决定趁此机 ...
随机推荐
- 封装HttpUrlConnection开箱即用
因为经常用到 便写出来方边使用 直接复制本类即可 import java.io.*; import java.net.HttpURLConnection; import java.net.URL; i ...
- zookeeper-分布式锁的代码实现-【每日五分钟搞定大数据】
本文涉及到几个zookeeper简单的知识点,永久节点.有序节点.watch机制.比较基础,熟悉的就别看了跳过这篇吧 每个线程在/locks节点下创建一个临时有序节点test_lock_0000000 ...
- 朱晔的互联网架构实践心得S1E4:简单好用的监控六兄弟
朱晔的互联网架构实践心得S1E4:简单好用的监控六兄弟 [下载本文PDF进行阅读] 这里所说的六兄弟只指ELK套件(ElasticSearch+Logstash+Kibana)以及TIG套件(Tele ...
- [书籍]重温《Framework Design Guidelines》
1. 前言 最近重温了<Framework Design Guidelines>. <Framework Design Guidelines>中文名称为<.NET设计规范 ...
- CF每日一练 Codeforces Round #520 (Div. 2)
比赛过程总结:过程中有事就玩手机了,后面打的状态不是很好,A题理解错题意,表明了内心不在状态,B题想法和思路都是完全正确的,但是并没有写出来,因为自己代码能力不强,思路不是特别清晰,把代码后面写乱了, ...
- python 的内存回收,及深浅Copy详解
一.python中的变量及引用 1.1 python中的不可变类型: 数字(num).字符串(str).元组(tuple).布尔值(bool<True,False>) 接下来我们讲完后你就 ...
- python安装与使用(Windows)
日常使用PHP开发较多,但是有些地方PHP的语言的瓶颈就显露出来了,例如,同样是抓取一个网站的内容,使用PHP需要较为复杂的正则匹配,效率较为低下.python具有丰富的类库,拿过来直接可以使用,功能 ...
- PHP之CLI模式
转载: http://www.cnblogs.com/zcy_soft/archive/2011/12/10/2283437.html 所有的PHP发行版,不论是编译自源代码的版本还是预创建的版本,都 ...
- awr format
AWR-Format工具 在Chrome高版本中配置使用AWR-Format for Chrome插件
- Oracle 表分区(Partition)
表分区功能能够改善应用程序性能,提高数据库可管理性和可用性,是数据库管理非常关键的技术.数据库通过使用分区提高查询性能,简化日常管理维护工作. 1 分区优点 1) 减少维护工作量,独立管理每个表分区比 ...
