[matlab] 23.matlab自带kmeans函数 实现聚类
clc,clear all;
point=[1.40000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.30000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.70000000000000,0.400000000000000;1.40000000000000,0.300000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.50000000000000,0.100000000000000;1.50000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.40000000000000,0.100000000000000;1.10000000000000,0.100000000000000;1.20000000000000,0.200000000000000;1.50000000000000,0.400000000000000;1.30000000000000,0.400000000000000;1.40000000000000,0.300000000000000;1.70000000000000,0.300000000000000;1.50000000000000,0.300000000000000;1.70000000000000,0.200000000000000;1.50000000000000,0.400000000000000;1,0.200000000000000;1.70000000000000,0.500000000000000;1.90000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.60000000000000,0.400000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.60000000000000,0.200000000000000;1.50000000000000,0.400000000000000;1.50000000000000,0.100000000000000;1.40000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.20000000000000,0.200000000000000;1.30000000000000,0.200000000000000;1.40000000000000,0.100000000000000;1.30000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.30000000000000,0.300000000000000;1.30000000000000,0.300000000000000;1.30000000000000,0.200000000000000;1.60000000000000,0.600000000000000;1.90000000000000,0.400000000000000;1.40000000000000,0.300000000000000;1.60000000000000,0.200000000000000;1.40000000000000,0.200000000000000;1.50000000000000,0.200000000000000;1.40000000000000,0.200000000000000;4.70000000000000,1.40000000000000;4.50000000000000,1.50000000000000;4.90000000000000,1.50000000000000;4,1.30000000000000;4.60000000000000,1.50000000000000;4.50000000000000,1.30000000000000;4.70000000000000,1.60000000000000;3.30000000000000,1;4.60000000000000,1.30000000000000;3.90000000000000,1.40000000000000;3.50000000000000,1;4.20000000000000,1.50000000000000;4,1;4.70000000000000,1.40000000000000;3.60000000000000,1.30000000000000;4.40000000000000,1.40000000000000;4.50000000000000,1.50000000000000;4.10000000000000,1;4.50000000000000,1.50000000000000;3.90000000000000,1.10000000000000;4.80000000000000,1.80000000000000;4,1.30000000000000;4.90000000000000,1.50000000000000;4.70000000000000,1.20000000000000;4.30000000000000,1.30000000000000;4.40000000000000,1.40000000000000;4.80000000000000,1.40000000000000;5,1.70000000000000;4.50000000000000,1.50000000000000;3.50000000000000,1;3.80000000000000,1.10000000000000;3.70000000000000,1;3.90000000000000,1.20000000000000;5.10000000000000,1.60000000000000;4.50000000000000,1.50000000000000;4.50000000000000,1.60000000000000;4.70000000000000,1.50000000000000;4.40000000000000,1.30000000000000;4.10000000000000,1.30000000000000;4,1.30000000000000;4.40000000000000,1.20000000000000;4.60000000000000,1.40000000000000;4,1.20000000000000;3.30000000000000,1;4.20000000000000,1.30000000000000;4.20000000000000,1.20000000000000;4.20000000000000,1.30000000000000;4.30000000000000,1.30000000000000;3,1.10000000000000;4.10000000000000,1.30000000000000;6,2.50000000000000;5.10000000000000,1.90000000000000;5.90000000000000,2.10000000000000;5.60000000000000,1.80000000000000;5.80000000000000,2.20000000000000;6.60000000000000,2.10000000000000;4.50000000000000,1.70000000000000;6.30000000000000,1.80000000000000;5.80000000000000,1.80000000000000;6.10000000000000,2.50000000000000;5.10000000000000,2;5.30000000000000,1.90000000000000;5.50000000000000,2.10000000000000;5,2;5.10000000000000,2.40000000000000;5.30000000000000,2.30000000000000;5.50000000000000,1.80000000000000;6.70000000000000,2.20000000000000;6.90000000000000,2.30000000000000;5,1.50000000000000;5.70000000000000,2.30000000000000;4.90000000000000,2;6.70000000000000,2;4.90000000000000,1.80000000000000;5.70000000000000,2.10000000000000;6,1.80000000000000;4.80000000000000,1.80000000000000;4.90000000000000,1.80000000000000;5.60000000000000,2.10000000000000;5.80000000000000,1.60000000000000;6.10000000000000,1.90000000000000;6.40000000000000,2;5.60000000000000,2.20000000000000;5.10000000000000,1.50000000000000;5.60000000000000,1.40000000000000;6.10000000000000,2.30000000000000;5.60000000000000,2.40000000000000;5.50000000000000,1.80000000000000;4.80000000000000,1.80000000000000;5.40000000000000,2.10000000000000;5.60000000000000,2.40000000000000;5.10000000000000,2.30000000000000;5.10000000000000,1.90000000000000;5.90000000000000,2.30000000000000;5.70000000000000,2.50000000000000;5.20000000000000,2.30000000000000;5,1.90000000000000;5.20000000000000,2;5.40000000000000,2.30000000000000;5.10000000000000,1.80000000000000]; figure;
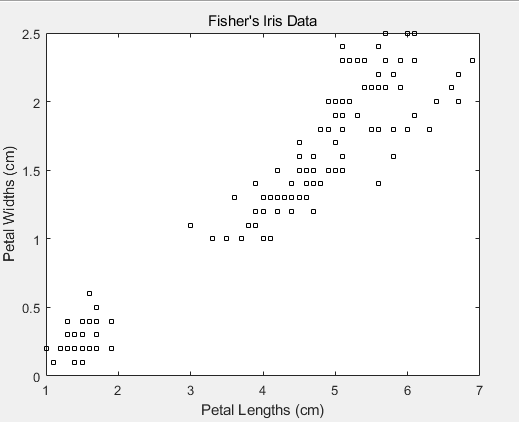
plot(point(:,1),point(:,2),'ks','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)'; rng(1); % For reproducibility
[idx,C] = kmeans(point,3); x1 = min(point(:,1)):0.01:max(point(:,1));
x2 = min(point(:,2)):0.01:max(point(:,2));
[x1G,x2G] = meshgrid(x1,x2);
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C); figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(point(:,1),point(:,2),'ks','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;
kmeans

rng default; % For reproducibility
X = [randn(100,2)*0.75+ones(100,2);
randn(100,2)*0.5-ones(100,2)]; figure(1);
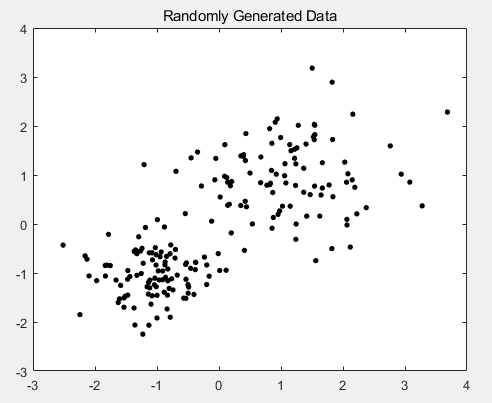
plot(X(:,1),X(:,2),'k.','MarkerSize',12);
title 'Randomly Generated Data'; opts = statset('Display','final');
[idx,C] = kmeans(X,2,'Distance','cityblock','Replicates',5,'Options',opts); %这里可以改聚类数量 figure(2);
plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)
hold on
plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)
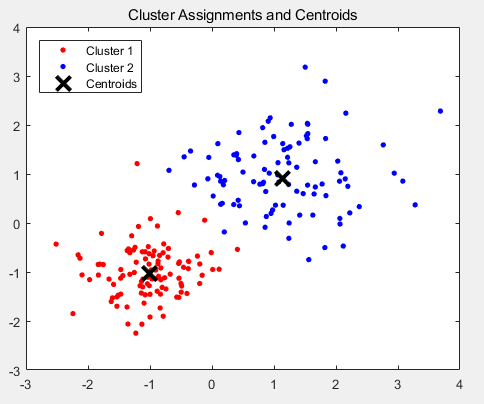
plot(C(:,1),C(:,2),'kx','MarkerSize',15,'LineWidth',3) %标记聚类中心
legend('Cluster 1','Cluster 2','Centroids','Location','NW')
title 'Cluster Assignments and Centroids'
hold off
kmeans
[matlab] 23.matlab自带kmeans函数 实现聚类的更多相关文章
- matlab学习-使用自带的函数
>> %定义矩阵求最大值>> a=[1 7 3;6 2 9];>> A=max(a);>> a a = 1 7 3 6 2 9 >> A A ...
- MATLAB实现最优低通滤波器的函数
MATLAB实现最优低通滤波器的函数 % Fs --Data rate % Fpass --pass band % Fstop --Cutoff frequencies % Apass ...
- 数学建模及机器学习算法(一):聚类-kmeans(Python及MATLAB实现,包括k值选取与聚类效果评估)
一.聚类的概念 聚类分析是在数据中发现数据对象之间的关系,将数据进行分组,组内的相似性越大,组间的差别越大,则聚类效果越好.我们事先并不知道数据的正确结果(类标),通过聚类算法来发现和挖掘数据本身的结 ...
- [转]matlab语言中的assert断言函数
MATLAB语言没有系统的断言函数,但有错误报告函数 error 和 warning.由于要求对参数的保护,需要对输入参数或处理过程中的一些状态进行判断,判断程序能否/是否需要继续执行.在matlab ...
- 【matlab】MATLAB程序调试方法和过程
3.8 MATLAB程序的调试和优化 在MATLAB的程序调试过程中,不仅要求程序能够满足设计者的设计需求,而且还要求程序调试能够优化程序的性能,这样使得程序调试有时比程序设计更为复杂.MATLAB ...
- Easyui中 alert 带回调函数的 消息框
带回调函数的 消息框: $.messager.alert({ title:'消息', msg:'电话号码 只能是数字!', icon: 'info', width: 300, top:200 , // ...
- 定时器(setTimeout/setInterval)调用带参函数失效解决方法
也许你曾碰到过这样的问题,不管是setInterval()还是setTimeout(),当code参数里放一个带参函数时,定时器都会失效,看下面这个例子: function test(str){ al ...
- 第7.23节 Python使用property函数定义属性简化属性访问的代码实现
第7.23节 Python使用property函数定义属性简化属性访问的代码实现 一. 背景 在本章前面章节中,我们介绍了类相关的知识,并举例进行了说明,在这些例子中会定义一些形如 ...
- Python实现kMeans(k均值聚类)
Python实现kMeans(k均值聚类) 运行环境 Pyhton3 numpy(科学计算包) matplotlib(画图所需,不画图可不必) 计算过程 st=>start: 开始 e=> ...
随机推荐
- webpack4 系列教程(十二):处理第三方JavaScript库
教程所示图片使用的是 github 仓库图片,网速过慢的朋友请移步<webpack4 系列教程(十二):处理第三方 JavaScript 库>原文地址.或者来我的小站看更多内容:godbm ...
- mybatis类型别名
在mybatis中,statement的parameterType指定了输入参数的类型,resultType指定了输出结果的映射类型可以针对parameterType或resultType中指定的类型 ...
- WORLD 目录排版调整
文本如下: ----------------------------------------------------------------- 前言1 简介2 我爱你3 圣灵丹方士大夫4 阿类似的看风 ...
- 2018-09-24 Java源码英翻中网页演示
在线演示地址: 源代码翻译 两部分如下. 独立的Java代码翻译库 续前文代码翻译尝试-使用Roaster解析和生成Java源码 源码库: program-in-chinese/java_code_t ...
- iphone怎么投屏到电脑屏幕上
随着苹果手机的更显换代,苹果手机的功能越来越强大,其中iphone手机更新了airplay镜像功能,所以想要手机投屏电脑的小伙伴就更加方便了,但是iphone怎么投屏到电脑呢?大家不用着急,下面即将为 ...
- java排序算法之希尔排序
希尔排序是冲破二次时间屏障的第一批算法之一. 它是通过比较相距一定间隔的元素来工作,各趟比较所用的距离随着算法的进行而减小,直到最后一趟(比较相邻元素)为止.因此希尔排序也叫缩减增量排序. 希尔排序使 ...
- zxing开源库的基本使用
如果你的项目中有模块跟二维码相关的话,那你一定听过或者用过大名鼎鼎的zxing开源库. 什么是zxing? ZXing是一个开源的,用Java实现的多种格式的1D/2D条码图像处理库,它包含了联系到其 ...
- Android ScrollView内部组件设置android:layout_height="fill_parent"无效的解决办法
问题:scrollview内部组件都设置了android:layout_height="fill_parent"却没有效果. 解决办法:设置scrollview的fillViewp ...
- Flutter 布局(三)- FittedBox、AspectRatio、ConstrainedBox详解
本文主要介绍Flutter布局中的FittedBox.AspectRatio.ConstrainedBox,详细介绍了其布局行为以及使用场景,并对源码进行了分析. 1. FittedBox Scale ...
- seajs的原理以及基本使用
seajs模块化开发 模块化开发,把整个文件分割成一个一个小文件. 使用方法 使用方法特别简单,首先在官网中下载sea.js,然后在页面中引入. index.html // 1.路径 // 2.回调 ...
