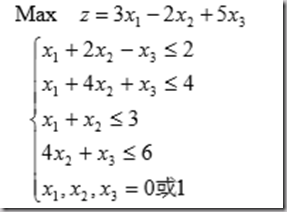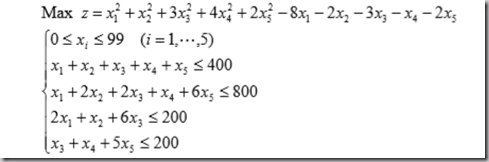【数学建模】day02-整数规划
基本类似于中学讲的整数规划--线性规划中变量约束为整数的情形。
目前通用的解法适合整数线性规划。不管是完全整数规划(变量全部约束为整数),还是混合整数规划(变量既有整数又有实数),MATLAB都提供了通用的求解函数。
一、0-1型整数规划
这类规划将变量限制为0和1,有时候多个规划问题可以通过引入0-1变量将问题统一在一个规划问题中讨论。例如:
拥有相互排斥的规划约束:
一般的,
二、0-1整数规划的一个解法:隐枚举法
因为变量的取值是取0-1的,所以可以枚举所有取值求得极大/极小值。例如,求解
(1)试探一个可行解(x1,x2,x3)=(1,0,0),相应的目标函数值是3。暂做最优解。
(2)继续试探其他可行解。倘若目标函数值小于3则不考虑,这相当于增加了目标大于等于3的又一个约束。否则目标函数值大于3,则新的可行解暂做最优解,更新当前最优目标函数值,重复(2)。
(3)直到:枚举完所有可行解。
三、固定费用问题
举例说明这类问题是:有三种产品投资方式,相应增加A产品投资会使得A的固定成本上升,而由于产品产量增加使得单个产品费用下降,问如何投资使得成本最低。
解决这个问题的一个方法可以是:列成本函数,引入0-1变量统一到一个规划问题中。具体求解不赘述。
四、非线性整数规划的一个方法:蒙特卡洛法
尽管整数规划由于限制变量为整数而增加了难度;然而又由于整数解是有限个,于是为枚举法提供了方便。
当然,当自变量维数很大和取值范围很宽情况下,企图用显枚举法(即穷举法)计算出优值是不现实的,但是应用概率理论可以证明,在一定的计算量的情况下(这里指蒙特卡罗法随机抽取可行点求解近似解),完全可以得出一个满意解。
所谓蒙特卡洛法(随机取样),是指对于计算量过大的问题,通过随机取样计算部分,而非整体,来降低计算量的方法。这通常是近似解,但概率统计的方法证明,这是可靠的。
蒙特卡洛的应用实例。
(1)计算面积:计算y=x^2,y=12-x与x轴在第一象限围城的曲边三角形的面积。
方法:利用蒙特卡罗法。在矩形(0,0),(0,9),(12,9),(12,0)中随机生成n个点,统计落在曲边三角形内的点个数,计算频度即为曲边三角形与矩形的面积之比。
使用 matlab生成一维均匀分布随机数: R = unifrnd(A,B):生成区间(A,B)内的随机数,A,B可以是向量。 R = unifrnd(A,B,M,N):生成区间(A,B)内的M*N个随机数。 R = unifrnd(A,B,[M,N]):同上。 生成二维均匀分布随机数则由一维组合而成。matlab实现:
clc,clear
x = unifrnd(,,,);
y = unifrnd(,,,);
pinshu = sum(y<x.^ & x<=) + sum(x> & y <-x);
area = pinshu/**;
area
(2)一个非线性规划蒙特卡洛求解实例
使用: 产生随机数种子:为了防止相同状态开始会产生相同的伪随机数(特别是程序中有loop) . rand('state',sum(*clock)):根据当前时间,已经不推荐使用 . rand('twister',mod(floor(now*),^-)):也可以 . rng命令注:
实现:
先定义函数:
function [f,g] = mente(x)
f=x()^+x()^+*x()^+*x()^+*x()-*x()-*x()-*x() -x()-*x();
g=[sum(x)- x()+*x()+*x()+x()+*x()- *x()+x()+*x()- x()+x()+*x()-];再求解:
clc,clear
rand('state',sum(clock));
p0 = ;
tic
for i = :^
x = *rand(,); %rand(,)生成5行1列0-1上的均匀分布随机数
x1 = floor(x);
x2 = ceil(x);
[f,g] = mente(x1);
if sum(g<=) ==
if p0 <= f
x0 = x1;
p0 = f;
end
end
[f,g] = mente(x2);
if sum(g<=)==
if p0<=f
x0 = x2;
p0 = f;
end
end
end
x0
p0
toc五、指派问题
分配n人去做n个任务,每人做且只做一项任务。第i个人做第j项任务,花费cij时间。问如何分配人去做任务,使得总时间花费最少。
可以看出,花费cij构成矩阵,称为指派矩阵。引入0-1变量矩阵n*n,则该矩阵每行每列只有一个1,其余为0,为1代表i做任务j,转化为一个整数规划问题。
匈牙利算法可解。
六、整数规划的matlab通用解法
函数:
[x,fval] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)
param:
f:目标函数系数列向量
intcon:整数变量的地址,如变量有x1,x2,x3,若x2,x3为整数变量,则intcon = 2:3
A,b对应不等约束
Aeq,beq对应等式约束
lb,ub对应边界约束
return:
x:取得最优值的对应变量取值
fval:最优值。同理,这是求标准型即min,若求max则目标函数求反
求解实例:
(1)求解指派问题:已知指派矩阵为
clc,clear
c = [ ;
;
;
;
];
c = c(:);
a = zeros(,);
intcon = :;
for i = :
%这是把二维矩阵转换成一维,要满足一个人只做一个任务,一个任务只被一个人做的等式条件,共5*2个条件
a(i,(i-)*+:*i)=;
a(+i,i::)=;
end
b = ones(,);
lb = zeros(,);
ub = ones(,);
[x,y] = intlinprog(c,intcon,[],[],a,b,lb,ub);
x = reshape(x,[,])
也就是相应C矩阵,取xij1则对应i做任务j。
(2)求解混合整数规划问题
min z = –3x1 –2x2 – x3
s.t.
x1 + x2 + x3 <=7,
4x1 + 2x2 + x3 =12,
x1,x2 >=0
x3 = 0或1
分析知,只有x3是0-1整数变量,则intcon = 3
求解:
clc,clear
f = [-;-;-];
A = [,,];
b = ;
Aeq = [,,];
beq = ;
lb = zeros(,);
ub = [inf;inf;];
intcon = ;
[x,y] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub);
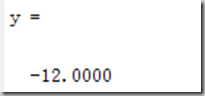
x
y
【数学建模】day02-整数规划的更多相关文章
- Python小白的数学建模课-04.整数规划
整数规划与线性规划的差别只是变量的整数约束. 问题区别一点点,难度相差千万里. 选择简单通用的编程方案,让求解器去处理吧. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达 ...
- BITED数学建模七日谈之二:怎样阅读数学模型教材
今天进入我们数学建模七日谈的第二天:怎样阅读数学建模教材? 大家再学习数学建模这门课程或准备比赛的时候,往往都是从教材开始的,教材的系统性让我们能够很快,很深入地了解前人在数学模型方面已有的研究成果, ...
- 【数学建模】线性规划各种问题的Python调包方法
关键词:Python.调包.线性规划.指派问题.运输问题.pulp.混合整数线性规划(MILP) 注:此文章是线性规划的调包实现,具体步骤原理请搜索具体解法. 本文章的各个问题可能会采用多种调用方 ...
- Python数学建模-01.新手必读
Python 完全可以满足数学建模的需要. Python 是数学建模的最佳选择之一,而且在其它工作中也无所不能. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数学 ...
- Python数学建模-02.数据导入
数据导入是所有数模编程的第一步,比你想象的更重要. 先要学会一种未必最佳,但是通用.安全.简单.好学的方法. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数据导入 ...
- Python小白的数学建模课-A1.2021年数维杯C题(运动会优化比赛模式探索)探讨
Python小白的数学建模课 A1-2021年数维杯C题(运动会优化比赛模式探索)探讨. 运动会优化比赛模式问题,是公平分配问题 『Python小白的数学建模课 @ Youcans』带你从数模小白成为 ...
- Python小白的数学建模课-03.线性规划
线性规划是很多数模培训讲的第一个算法,算法很简单,思想很深刻. 要通过线性规划问题,理解如何学习数学建模.如何选择编程算法. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛 ...
- Python小白的数学建模课-05.0-1规划
0-1 规划不仅是数模竞赛中的常见题型,也具有重要的现实意义. 双十一促销中网购平台要求二选一,就是互斥的决策问题,可以用 0-1规划建模. 小白学习 0-1 规划,首先要学会识别 0-1规划,学习将 ...
- Python小白的数学建模课-A3.12 个新冠疫情数模竞赛赛题与点评
新冠疫情深刻和全面地影响着社会和生活,已经成为数学建模竞赛的背景帝. 本文收集了与新冠疫情相关的的数学建模竞赛赛题,供大家参考,欢迎收藏关注. 『Python小白的数学建模课 @ Youcans』带你 ...
- Python小白的数学建模课-06 固定费用问题
Python 实例介绍固定费用问题的建模与求解. 学习 PuLP工具包中处理复杂问题的快捷使用方式. 『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人. 前文讲到几种典型 ...
随机推荐
- Hadoop Yarn调度器的选择和使用
一.引言 Yarn在Hadoop的生态系统中担任了资源管理和任务调度的角色.在讨论其构造器之前先简单了解一下Yarn的架构. 上图是Yarn的基本架构,其中ResourceManager是整个架构的核 ...
- Nginx(一)------简介与安装
说到 Nginx ,可能大家最先想到的就是其负载均衡以及反向代理的功能.没错,这也是当前使用 Nginx 最频繁的两个功能,但是 Nginx 可不仅仅只有这两个功能,其作用还是挺大的,本系列博客就来慢 ...
- java基础 容器 API
- 断路器(Curcuit Breaker)模式
在分布式环境下,特别是微服务结构的分布式系统中, 一个软件系统调用另外一个远程系统是非常普遍的.这种远程调用的被调用方可能是另外一个进程,或者是跨网路的另外一台主机, 这种远程的调用和进程的内部调用最 ...
- Python_每日习题_0002_个税计算
# 题目 企业发放的奖金根据利润提成.利润(I)低于或等于10万元时, # 奖金可提10%:利润高于10万元,低于20万元时,低于10万元的部分按10%提成, # 高于10万元的部分,可提成7.%:2 ...
- 关于XLL加载项动态加载、卸载的演示及XLL函数自定义类型注册的演示
1.在XLL中,把函数定义成不同的类型,在Excel中的实际效果也不同,具体如下: pxMacroType value ...
- elasticsearch5.0版本的head安装
elasticsearch5.0版本的head安装 elasticsearch5.0版本由于刚出不久,并且与2.0版本的差距较大.所以,目前大家对5.0的一些使用还有所陌生.这里先把关于head插件的 ...
- html总结:背景图片拉伸
两种方法: ⑴推荐方法 <style>body {background-image:url(images/backimage.jpg);background-size:cover;}< ...
- Linux下破解pycharm
1.下载 https://pan.baidu.com/s/119UO4SGIEW_cxf0LmZzx3w 并将 JetbrainsCrack-3.1-release-enc.jar 放置到 pycha ...
- PHP开发编码规范
(转载:https://blog.csdn.net/alexdream/article/details/2213313) 这些年来多从事Linux下PHP和C相关的开发,带过很多项目和团队,下面是根据 ...