BZOJ2671 Calc（莫比乌斯反演）

　　两个多月之前写的题，今天因为看到一道非常相似的题就翻出来了，发现完全不会，没救。

　　感觉这个题其实第一步是最难想到的，也是最重要的。

　　设d=gcd(a,b)。那么a=yd，b=xd，且gcd(x,y)=1。a+b|ab等价于x+y|xyd。

　　由gcd(x,y)=1，得gcd(x+y,y)=gcd(x,x+y)=1。x和y都与x+y互质，那么他们的积xy也与x+y互质，即gcd(xy,x+y)=1。

　　gcd(xy,x+y)=1，而x+y|xyd，所以x+y|d。

　　那么现在要求的是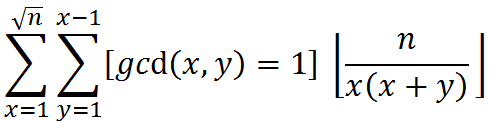

　　下取整的那部分是满足x+y|d且xd<=n的d的个数。

　　显然x>√n之后就没有贡献了。这样复杂度变为线性（不算gcd复杂度的话），但还不够。

　　看到那个gcd=1，妥妥的上莫比乌斯反演。接下来比较套路。

　　

　　

　　

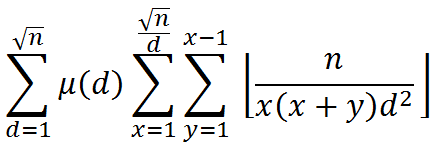
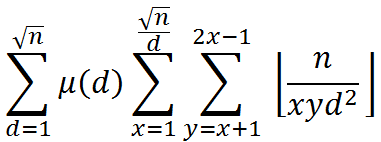
　　后面一部分的计算可以整除分块。

　　那这样的时间复杂度是多少呢？看起来是低于线性的，但具体是多少我也不知道……总之他跑的比香港记者还非常快。

　　今天看到的那道题多了一个限制，即ab/(a+b)与gcd(a,b)互质。

　　设c=ab/(a+b)，那么有(x+y)c=xyd。设d=k(x+y),c=kxy。由gcd(d,c)=1，如果能证明k是正整数的话，那么显然k=1。下证k为正整数。

　　反证。假设k=u/v(u,v∈N*,gcd(u,v)=1,v>1)。因为c，d均为正整数，所以v|x+y，v|xy。而又有gcd(x+y,xy)=1，矛盾。所以k为正整数。

　　剩下部分就类似了，由于确定了k=1即d=x+y，可以做到严格的√nlogn。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
using namespace std;
#define N 100000
#define min(a,b) ((a)<(b)?(a):(b))
#define ri register int
int n,m,mobius[N],prime[N],cnt=;
long long ans=;
bool flag[N];
int main()
{
    cin>>n;
    m=sqrt(n);
    flag[]=;mobius[]=;
    for (int i=;i<=m;i++)
    {
        if (!flag[i]) prime[++cnt]=i,mobius[i]=-;
        for (int j=;j<=cnt&&prime[j]*i<=m;j++)
        {
            flag[prime[j]*i]=;
            if (i%prime[j]==) break;
            else mobius[prime[j]*i]=-mobius[i];
        }
    }
    for (ri i=;i<=m;i++)
    if (mobius[i])
    {
        ri v=i*i,c=m/i+;
        for (ri k=;k<c;k++)
        {
            ri t=n/(k*v),u=(k<<)-,h=min(t,u)+;
            for (ri j=k+;j<h;)
            {
                ri w=t/j,l=min(u,t/w)+;
                ans+=1ll*(l-j)*mobius[i]*w;
                j=l;
            }
        }
    }
    cout<<ans;
}