Codeforces Round #404 (Div. 2) E. Anton and Permutation（树状数组套主席树 求出指定数的排名）

E. Anton and Permutation

time limit per test

4 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Anton likes permutations, especially he likes to permute their elements. Note that a permutation of n elements is a sequence of numbers {a₁, a₂, ..., a_n}, in which every number from 1 to n appears exactly once.

One day Anton got a new permutation and started to play with it. He does the following operation q times: he takes two elements of the permutation and swaps these elements. After each operation he asks his friend Vanya, how many inversions there are in the new permutation. The number of inversions in a permutation is the number of distinct pairs (i, j) such that 1 ≤ i < j ≤ n and a_i > a_j.

Vanya is tired of answering Anton's silly questions. So he asked you to write a program that would answer these questions instead of him.

Initially Anton's permutation was {1, 2, ..., n}, that is a_i = i for all i such that 1 ≤ i ≤ n.

Input

The first line of the input contains two integers n and q (1 ≤ n ≤ 200 000, 1 ≤ q ≤ 50 000) — the length of the permutation and the number of operations that Anton does.

Each of the following q lines of the input contains two integers l_i and r_i (1 ≤ l_i, r_i ≤ n) — the indices of elements that Anton swaps during the i-th operation. Note that indices of elements that Anton swaps during the i-th operation can coincide. Elements in the permutation are numbered starting with one.

Output

Output q lines. The i-th line of the output is the number of inversions in the Anton's permutation after the i-th operation.

Examples

Input

5 4
4 5
2 4
2 5
2 2

Output

1
4
3
3

Input

2 1
2 1

Output

1

Input

6 7
1 4
3 5
2 3
3 3
3 6
2 1
5 1

Output

5
6
7
7
10
11
8

Note

Consider the first sample.

After the first Anton's operation the permutation will be {1, 2, 3, 5, 4}. There is only one inversion in it: (4, 5).

After the second Anton's operation the permutation will be {1, 5, 3, 2, 4}. There are four inversions: (2, 3), (2, 4), (2, 5) and (3, 4).

After the third Anton's operation the permutation will be {1, 4, 3, 2, 5}. There are three inversions: (2, 3), (2, 4) and (3, 4).

After the fourth Anton's operation the permutation doesn't change, so there are still three inversions.

【分析】题意很简单，就是动态的求区间逆序数。当时没做出来，赛后看了题解，学了发树状数组套主席树（内层主席树外层树状数组）学了一上午=_=借这个题好好说一下我对这个的理解吧，有啥不对的希望大佬能指出来OTZ.

主席树套树状数组就是梳妆数组的每一个节点都是一颗主席树，可以理解为线段树吧。主席树可以静态的求出排名，而动态的可以借助树状数组求，logn。而对于每一棵主席树，从i~n一棵一棵的建，可以这么理解，其实每一棵树都是一样的，包括所有的节点，只是有些节点隐藏起来了，只显现了一部分，显现了哪些部分呢?这就要考虑到树状数组了。树状数组的每一个节点，都与一个lowbit有关，刷过树状数组的应该知道，见下图

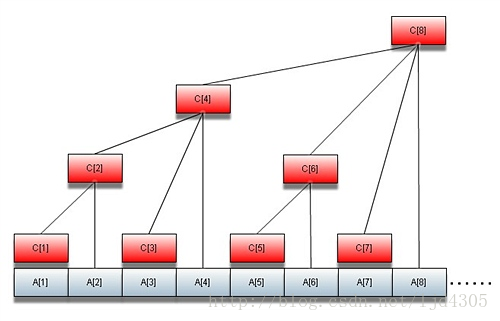
比如说对于4节点，（对于这个题目）初始就只显现了1~4区间的值。而对于6节点就之显现了5~6节点，注意，我这里说的是初始阶段。好嘞，现在来说修改。比如说我要把num[2]和num[6]换一下，那我们就把第二个节点的num[6]点亮（即显现），怎么点亮了？注意，我们一开始是按照从小到大的顺序存的，即每一刻主席树的叶子节点（包括未显现的）从左到右-->从小到大，那么就可以在lson,rson里找了，复杂度logn。找到之后就点亮,sz[]++.然后往上lowbit，将所有与之相关的节点的主席树相关位置都做同样的修改，复杂度logn。现在说查询，树状数组的查询会吧，就是lowbit求前缀和嘛，这个也一样，从上往下求lowbit前缀。对于每一刻主席树，先找到这个值，然后这个值（叶子节点）左边的叶子节点个数即是这棵书中比他小的，然后把所有相关的lowbit节点的线段树（不重合）的所有比他小的值得个数加起来，logn*logn。

嗯。。。这差不多就是我的理解了，要是有啥不对的，请大佬一定要指出来呀，嘻嘻。。。

听说还有一种叫 分块 的东西比这个简单，明天就学，学会了再写个做法，嘻嘻。。。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <stack>
#include <queue>
#include <vector>
#include <map>
#define inf 0x3f3f3f3f
#define met(a,b) memset(a,b,sizeof a)
#define pb push_back
using namespace std;
typedef long long ll;
const int N = 2e7+;
int sz[N],lson[N],rson[N],num[N],bit[N],n,total;
int addson() {return ++total;}
int lowbit(int x) {return x&(-x);}
void add(int &x,int l,int r,int y,int z){
    if (!x)x=addson();
    sz[x]+=z;
    if (l==r) return;
    int mid=(l+r)>>;
    if (y<=mid) add(lson[x],l,mid,y,z);
    else add(rson[x],mid+,r,y,z);
}
int ask(int x,int l,int r,int y){
    if (!x) return ;
    if (l==r) return sz[x];
    int mid=(l+r)>>;
    if (y<=mid) return ask(lson[x],l,mid,y);
    else return sz[lson[x]]+ask(rson[x],mid+,r,y);
}
ll bigask(int x,int y){
    ll now=;
    while (x) {
        now+=ask(bit[x],,n,y);
        x-=lowbit(x);
    }
    return now;
}
void bigadd(int x,int y,int z){
    while (x<=n) {
        add(bit[x],,n,y,z);
        x+=lowbit(x);
    }
}
int main(){
    int m;
    scanf("%d%d",&n,&m);
    ll sum=;
    for(int i=;i<=n;i++)bigadd(i,num[i]=i,);
    while (m--) {
        int l,r;
        scanf("%d %d",&l,&r);
        if (l==r) {
            printf("%lld\n",sum);
            continue;
        }
        if (l>r)swap(l,r);
        if (r-l>) {
            sum-=*(bigask(r-,num[l])-bigask(l,num[l]));
            sum+=*(bigask(r-,num[r])-bigask(l,num[r]));
        }
        if (num[l]<num[r]) ++sum;
        else --sum;
        printf("%lld\n",sum);
        bigadd(l,num[l],-);
        bigadd(l,num[r],);
        bigadd(r,num[r],-);
        bigadd(r,num[l],);
        swap(num[l],num[r]);
    }
    return ;
}