183.Wood Cut【hard】

183.Wood Cut【hard】

Given n pieces of wood with length L[i] (integer array). Cut them into small pieces to guarantee you could have equal or more than k pieces with the same length. What is the longest length you can get from the n pieces of wood? Given L & k, return the maximum length of the small pieces.

Notice

You couldn't cut wood into float length.

If you couldn't get >= k pieces, return 0.

Example

For L=[232, 124, 456], k=7, return 114.

Challenge

O(n log Len), where Len is the longest length of the wood.

这个题一上来一点思路没有，参考：https://algorithm.yuanbin.me/zh-hans/binary_search/wood_cut.html里面的思路

这道题要直接想到二分搜素其实不容易，但是看到题中 Challenge 的提示后你大概就能想到往二分搜索上靠了。首先来分析下题意，题目意思是说给出 n 段木材L[i], 将这 n 段木材切分为至少 k 段，这 k 段等长，求能从 n 段原材料中获得的最长单段木材长度。以 k=7 为例，要将 L 中的原材料分为7段，能得到的最大单段长度为114, 232/114 = 2, 124/114 = 1, 456/114 = 4, 2 + 1 + 4 = 7。

理清题意后我们就来想想如何用算法的形式表示出来，显然在计算如2, 1, 4等分片数时我们进行了取整运算，在计算机中则可以使用下式表示：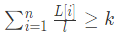

其中 l 为单段最大长度，显然有 1 ≤ l ≤ max(L[i]). 单段长度最小为1，最大不可能超过给定原材料中的最大木材长度。

Warning 注意求和与取整的顺序，是先求 L[i]/l的单个值，而不是先对L[i]求和。

分析到这里就和题 sqrt(x) 差不多一样了，要求的是 l 的最大可能取值，同时 l 可以看做是从有序序列[1, max(L[i])]的一个元素，典型的二分搜素！

代码参考了：http://www.jiuzhang.com/solution/wood-cut/

解法一：

 public class Solution {
     /**
      *@param L: Given n pieces of wood with length L[i]
      *@param k: An integer
      *return: The maximum length of the small pieces.
      */
     public int woodCut(int[] L, int k) {
         int max = ;
         for (int i = ; i < L.length; i++) {
             max = Math.max(max, L[i]);
         }

         // find the largest length that can cut more than k pieces of wood.
         int start = , end = max;
         while (start +  < end) {
             int mid = start + (end - start) / ;
             if (count(L, mid) >= k) {
                 start = mid;
             } else {
                 end = mid;
             }
         }

         if (count(L, end) >= k) {
             return end;
         }
         if (count(L, start) >= k) {
             return start;
         }
         return ;
     }

     private int count(int[] L, int length) {
         int sum = ;
         for (int i = ; i < L.length; i++) {
             sum += L[i] / length;
         }
         return sum;
     }
 }

对于上面发现还有可以优化的地方，那就是我们二分找长度的时候只需要找所有木块里面最短的即可，就是所谓的木桶原理，那么end上界又可以进一步减少。

解法二：

 class Solution {
 public:
     /*
      * @param L: Given n pieces of wood with length L[i]
      * @param k: An integer
      * @return: The maximum length of the small pieces
      */
     int woodCut(vector<int> &L, int k) {
         if (L.empty() || k <= ) {
             return ;
         }
         //get min
         int min = INT_MIN;
         for (int i = ; i < L.size(); ++i) {
             min = (min < L[i] ? L[i] : min);
         }

         int start = ;
         int end = min;

         while (start +  < end) {
             int mid = start + (end - start) / ;

             if (cal(L, mid) >= k) {
                 start = mid;
             }
             else {
                 end = mid;
             }
         }

         if (cal(L, end) >= k) {
             return end;
         }
         else if (cal(L, start) >= k) {
             return start;
         }
         else {
             return ;
         }
     }

     int cal(vector<int> & L, int len) {
         int sum = ;
         for (int i = ; i < L.size(); ++i) {
             sum += L[i] / len;
         }

         return sum;
     }
 };