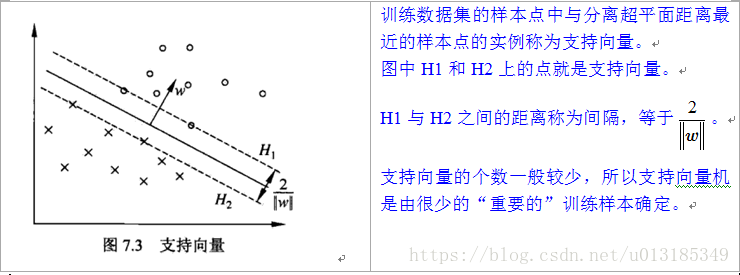
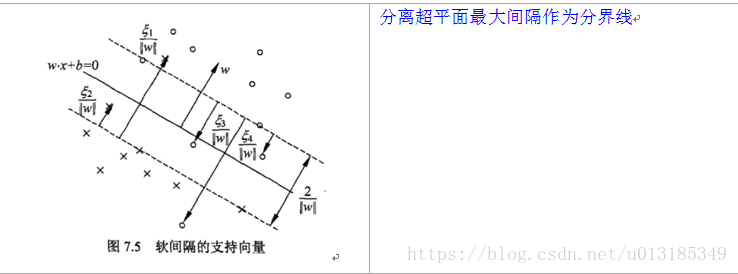
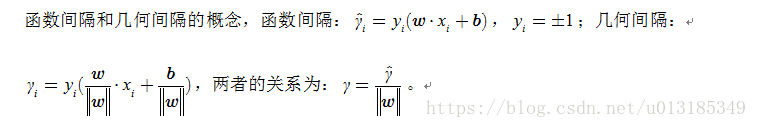SVM知识点

SVM(Support Vector Machine)，支持向量机，有监督学习模型，一种分类模型。在特征空间（输入空间为欧式空间或离散集合，特征空间为欧式空间或希尔伯特空间）中寻找间隔最大化的分离超平面的线性分类器。学习策略就是间隔最大化，可形式化为一个求解凸二次规划(QP)的问题，也等价于正则化的合页损失函数的最小化问题。

针对数据特点，处理方法或者说原理是：

(1).当训练样本线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分SVM；

(2).当训练数据近似线性可分时，引入松弛变量，通过软间隔最大化，学习一个线性分类器，即线性支持向量机；

(3).当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

一句话解释一下线性核和高斯核的区别：

Linear核主要用于线性可分的情形，参数少，速度快；高斯核主要用于线性不可分的情形，参数多，分类结果依赖于参数，可通过公式辨别。

1. 如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是LinearKernel的SVM

2. 如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel

3. 如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况

当样本在原始空间线性不可分时，将样本由原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。(高维空间线性可分)

通过核函数可以学习非线性支持向量机，等价于隐式地在高维的特征空间中学习线性支持向量机。即传说中的核方法。

为什么SVM对缺失数据敏感？

SVM没有处理缺失值的策略(决策树有)，SVM希望样本在特征空间中线性可分，所以特征空间的好坏对SVM性能很重要。

为什么使用间隔最大化：

线性可分支持向量机利用间隔最大化求得最优分离超平面，这时，解是存在且唯一的。另一方面，此时的分隔超平面所产生的分类结果是最鲁棒的，对未知实例的泛化能力最强。

为什么将SVM的原始问题转换为其对偶问题来解决：

因为对偶问题往往更容易求解，原问题的求解包含约束条件，使问题求解变得复杂，将目标函数和约束重新整合到一个新函数，即拉格朗日函数，然后再通过这个函数来寻找最优解比较容易。

具体求解过程见李航统计学习方法第七章。

SVM用到的Python库和调参：

Sklearn库，调用sklearn.svm，-c 惩罚参数；kernel：0为线性，1为多项式，2为RBF核，3为sigmoid(tanh)；gamma：核函数参数；coef0：核函数的常数项。

https://www.zhihu.com/question/21094489上的例子解释的很通俗易懂。