BZOJ.4695.最假女选手(线段树 Segment tree Beats!)

题目链接

区间取\(\max,\ \min\)并维护区间和是普通线段树无法处理的。

对于操作二，维护区间最小值\(mn\)、最小值个数\(t\)、严格次小值\(se\)。

当\(mn\geq x\)时，不需要改变，return；\(se>x>mn\)时，\(sum=sum+(x-mn)*t\)，打上区间\(\max\)标记；

当\(x\geq se>mn\)时，不会做，继续递归分别处理两个子区间，直到遇到前两种情况。

操作三同理，维护最大值、最大值个数、次大值。

复杂度\(O(m\log^2n)\)，常表现为\(O(m\log n)\)。通常叫做吉司机线段树。

[Update]

如果可以建值域线段树就好写多了。。（然而这题是区间查询）

对于取\(\max/\min\)操作可以直接区间修改清空超出范围的值，然后更新到对应位置上就行了（比如对\(v\)取\(\max\)，把\(\lt v\)的数全删掉，统计一下个数\(num\)，然后在\(v\)处加上\(num\)个\(v\)即可）。

复杂度\(m\log n\)，其实就是前/后缀的区间修改，也算和这题不太一样。

这样的题见BZOJ4399。

---

证明：（详见WC2016课件 Segment tree Beats!）

---

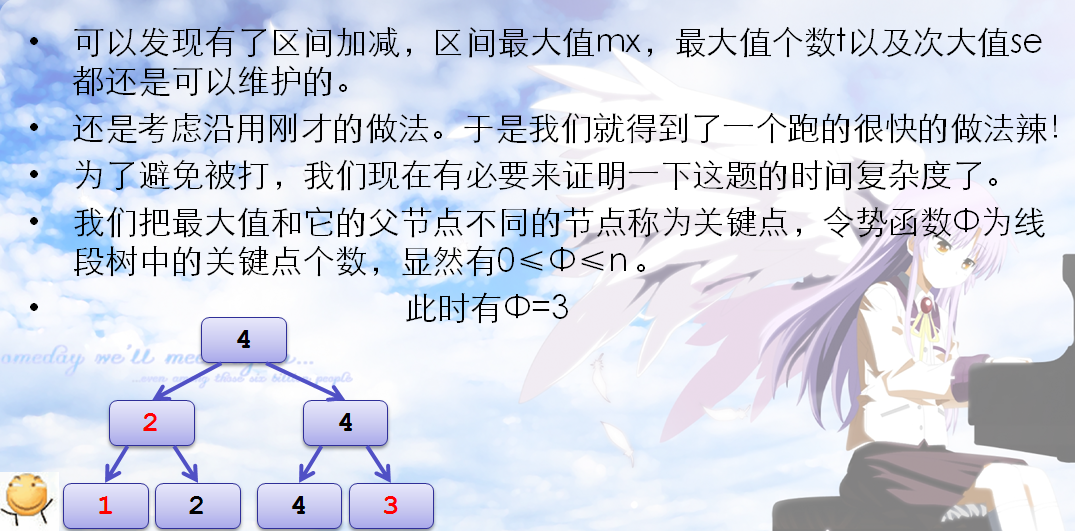
细节：

有两个修改(\(\max,\ \min\))，太恶心了。。

比如：取\(\min\)的时候不仅是改最大值，最小值也可能改（当然了...然而写这题的时候就是忘了）。

最大值改了\(\min\)标记也一定改（最大值是算了当前\(\min\)标记后的）。

还有\(\max\)标记也可能改，注意是取\(\min\)而不是直接赋值（还有加法影响这个标记，原先的最大值并不一定是由这个标记得到的）。

还有\(\min,\ \max\)可能会使得区间变为同一个数(第一句话的情况)，这就需要特判然后把\(sum\),次小值,次大值初始化掉。

还有如果\(mn\)没有跟\(mx\)一起变为\(v\)(上一种情况)，但是可能\(mn<v\geq se\)，还要让次小值取个\(\min\)。

还有常数太大。。考虑把\(\min,\ \max\)标记去掉，直接在父节点更新，并在适合的时候下传：\(47s\to 40s\).

调到怀疑线段树。。感谢manchery dalao的代码。

https://blog.csdn.net/u014609452/article/details/54912473

吐槽：机房电脑都31s过，bzoj给我卡到47s。。虽然开了O2吧，但秀一波学校大机房配置：



bzoj加油。

标记优化：

//79280kb	40460ms
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=5e5+5,INF=2e9;

char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
	int now=0,f=1;register char c=gc();
	for(;!isdigit(c);c=='-'&&(f=-1),c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now*f;
}

struct Segment_Tree
{
	#define S N<<2
	#define ls rt<<1
	#define rs rt<<1|1
	#define lson l,m,rt<<1
	#define rson m+1,r,rt<<1|1
	int mn[S],smn[S],tmn[S],mx[S],smx[S],tmx[S],sz[S],add[S];
	LL sum[S];
	#undef S
	inline void Update(int rt)
	{
		int l=ls,r=rs; sum[rt]=sum[l]+sum[r];
		if(mn[l]<mn[r]) mn[rt]=mn[l],smn[rt]=std::min(smn[l],mn[r]),tmn[rt]=tmn[l];
		else if(mn[l]>mn[r]) mn[rt]=mn[r],smn[rt]=std::min(smn[r],mn[l]),tmn[rt]=tmn[r];
		else mn[rt]=mn[l],smn[rt]=std::min(smn[l],smn[r]),tmn[rt]=tmn[l]+tmn[r];

		if(mx[l]>mx[r]) mx[rt]=mx[l],smx[rt]=std::max(smx[l],mx[r]),tmx[rt]=tmx[l];
		else if(mx[l]<mx[r]) mx[rt]=mx[r],smx[rt]=std::max(smx[r],mx[l]),tmx[rt]=tmx[r];
		else mx[rt]=mx[l],smx[rt]=std::max(smx[l],smx[r]),tmx[rt]=tmx[l]+tmx[r];
	}
	inline void Add(int x,int v)
	{
		add[x]+=v, mn[x]+=v, mx[x]+=v, sum[x]+=1ll*v*sz[x];
		if(smn[x]!=INF) smn[x]+=v;
		if(smx[x]!=-INF) smx[x]+=v;
	}
	inline void Min(int x,int v)
	{
//		if(v<mx[x])
		sum[x]-=1ll*tmx[x]*(mx[x]-v);
		mx[x]=v, mn[x]=std::min(mn[x],v);//!
		if(mn[x]==mx[x]) sum[x]=1ll*sz[x]*v, tmn[x]=tmx[x]=sz[x], smn[x]=INF, smx[x]=-INF;//!
		else smn[x]=std::min(smn[x],v);//!
	}
	inline void Max(int x,int v)
	{
//		if(v>mn[x])
		sum[x]+=1ll*tmn[x]*(v-mn[x]);
		mn[x]=v, mx[x]=std::max(mx[x],v);
		if(mn[x]==mx[x]) sum[x]=1ll*sz[x]*v, tmn[x]=tmx[x]=sz[x], smn[x]=INF, smx[x]=-INF;
		else smx[x]=std::max(smx[x],v);
	}
	void PushDown(int rt)
	{
		int l=ls,r=rs;
		if(add[rt]) Add(l,add[rt]), Add(r,add[rt]), add[rt]=0;
		if(mx[l]>mx[rt] && mx[rt]>smx[l]) Min(l,mx[rt]);//下传之前的min
		if(mx[r]>mx[rt] && mx[rt]>smx[r]) Min(r,mx[rt]);
		if(mn[l]<mn[rt] && mn[rt]<smn[l]) Max(l,mn[rt]);//下传之前的max
		if(mn[r]<mn[rt] && mn[rt]<smn[r]) Max(r,mn[rt]);
	}
	void Build(int l,int r,int rt)
	{
		sz[rt]=r-l+1;
		if(l==r)
		{
			tmn[rt]=tmx[rt]=1;
			sum[rt]=mn[rt]=mx[rt]=read(), smn[rt]=INF, smx[rt]=-INF;
			return;
		}
		Build(l,l+r>>1,ls), Build((l+r>>1)+1,r,rs);
		Update(rt);
	}
	void Modify_Add(int l,int r,int rt,int L,int R,int v)
	{
		if(L<=l && r<=R) {Add(rt,v); return;}
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m) Modify_Add(lson,L,R,v);
		if(m<R) Modify_Add(rson,L,R,v);
		Update(rt);
	}
	void Modify_Max(int l,int r,int rt,int L,int R,int v)
	{
		if(mn[rt]>=v) return;
		if(L<=l && r<=R && smn[rt]>v) {Max(rt,v); return;}
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m) Modify_Max(lson,L,R,v);
		if(m<R) Modify_Max(rson,L,R,v);
		Update(rt);
	}
	void Modify_Min(int l,int r,int rt,int L,int R,int v)
	{
		if(mx[rt]<=v) return;
		if(L<=l && r<=R && smx[rt]<v) {Min(rt,v); return;}
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m) Modify_Min(lson,L,R,v);
		if(m<R) Modify_Min(rson,L,R,v);
		Update(rt);
	}
	int Query_Max(int l,int r,int rt,int L,int R)
	{
		if(L<=l && r<=R) return mx[rt];
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m)
			if(m<R) return std::max(Query_Max(lson,L,R),Query_Max(rson,L,R));
			else return Query_Max(lson,L,R);
		else return Query_Max(rson,L,R);
	}
	int Query_Min(int l,int r,int rt,int L,int R)
	{
		if(L<=l && r<=R) return mn[rt];
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m)
			if(m<R) return std::min(Query_Min(lson,L,R),Query_Min(rson,L,R));
			else return Query_Min(lson,L,R);
		else return Query_Min(rson,L,R);
	}
	LL Query_Sum(int l,int r,int rt,int L,int R)
	{
		if(L<=l && r<=R) return sum[rt];
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m)
			if(m<R) return Query_Sum(lson,L,R)+Query_Sum(rson,L,R);
			else return Query_Sum(lson,L,R);
		else return Query_Sum(rson,L,R);
	}
}T;

int main()
{
	#define S 1,n,1
	int n=read(); T.Build(S);
	for(int m=read(),opt,l,r; m--; )
	{
		opt=read(),l=read(),r=read();
		if(opt==1) T.Modify_Add(S,l,r,read());
		else if(opt==2) T.Modify_Max(S,l,r,read());
		else if(opt==3) T.Modify_Min(S,l,r,read());
		else if(opt==4) printf("%lld\n",T.Query_Sum(S,l,r));
		else if(opt==5) printf("%d\n",T.Query_Max(S,l,r));
		else printf("%d\n",T.Query_Min(S,l,r));
	}
	#undef S
	return 0;
}

无优化：（靠fread卡过）

//94908kb	47472ms
#include <cstdio>
#include <cctype>
#include <algorithm>
//#define gc() getchar()
#define MAXIN 300000
#define gc() (SS==TT&&(TT=(SS=IN)+fread(IN,1,MAXIN,stdin),SS==TT)?EOF:*SS++)
typedef long long LL;
const int N=5e5+5,INF=2e9;

char IN[MAXIN],*SS=IN,*TT=IN;
inline int read()
{
	int now=0,f=1;register char c=gc();
	for(;!isdigit(c);c=='-'&&(f=-1),c=gc());
	for(;isdigit(c);now=now*10+c-'0',c=gc());
	return now*f;
}

struct Segment_Tree
{
	#define S N<<2
	#define ls rt<<1
	#define rs rt<<1|1
	#define lson l,m,rt<<1
	#define rson m+1,r,rt<<1|1
	int mn[S],smn[S],tmn[S],mx[S],smx[S],tmx[S],sz[S],add[S],tagmn[S],tagmx[S];
	LL sum[S];
	#undef S
	inline void Update(int rt)
	{
		int l=ls,r=rs; sum[rt]=sum[l]+sum[r];
		if(mn[l]<mn[r]) mn[rt]=mn[l],smn[rt]=std::min(smn[l],mn[r]),tmn[rt]=tmn[l];
		else if(mn[l]>mn[r]) mn[rt]=mn[r],smn[rt]=std::min(smn[r],mn[l]),tmn[rt]=tmn[r];
		else mn[rt]=mn[l],smn[rt]=std::min(smn[l],smn[r]),tmn[rt]=tmn[l]+tmn[r];

		if(mx[l]>mx[r]) mx[rt]=mx[l],smx[rt]=std::max(smx[l],mx[r]),tmx[rt]=tmx[l];
		else if(mx[l]<mx[r]) mx[rt]=mx[r],smx[rt]=std::max(smx[r],mx[l]),tmx[rt]=tmx[r];
		else mx[rt]=mx[l],smx[rt]=std::max(smx[l],smx[r]),tmx[rt]=tmx[l]+tmx[r];
	}
	inline void Add(int x,int v)
	{
		add[x]+=v, mn[x]+=v, mx[x]+=v, sum[x]+=1ll*v*sz[x];
		if(smn[x]!=INF) smn[x]+=v;
		if(smx[x]!=-INF) smx[x]+=v;
		if(tagmn[x]!=INF) tagmn[x]+=v;
		if(tagmx[x]!=-INF) tagmx[x]+=v;
	}
	inline void Min(int x,int v)
	{
		if(v<mx[x])
		{
			sum[x]-=1ll*tmx[x]*(mx[x]-v);
			mx[x]=v, mn[x]=std::min(mn[x],v);//!
			tagmn[x]=v/*! 首先要比最大值小才可能（且一定会）更新min标记*/,
			tagmx[x]=std::min(tagmx[x],v);//!
			if(mn[x]==mx[x]) sum[x]=1ll*sz[x]*v, tmn[x]=tmx[x]=sz[x], smn[x]=INF, smx[x]=-INF;//!
			else smn[x]=std::min(smn[x],v);//!
		}
	}
	inline void Max(int x,int v)
	{
		if(v>mn[x])
		{
			sum[x]+=1ll*tmn[x]*(v-mn[x]);
			mn[x]=v, mx[x]=std::max(mx[x],v);
			tagmx[x]=v, tagmn[x]=std::max(tagmn[x],v);
			if(mn[x]==mx[x]) sum[x]=1ll*sz[x]*v, tmn[x]=tmx[x]=sz[x], smn[x]=INF, smx[x]=-INF;
			else smx[x]=std::max(smx[x],v);
		}
	}
	void PushDown(int rt)
	{
		if(add[rt]) Add(ls,add[rt]), Add(rs,add[rt]), add[rt]=0;
		if(tagmn[rt]!=INF) Min(ls,tagmn[rt]), Min(rs,tagmn[rt]), tagmn[rt]=INF;
		if(tagmx[rt]!=-INF) Max(ls,tagmx[rt]), Max(rs,tagmx[rt]), tagmx[rt]=-INF;
	}
	void Build(int l,int r,int rt)
	{
		sz[rt]=r-l+1, tagmn[rt]=INF, tagmx[rt]=-INF;
		if(l==r)
		{
			tmn[rt]=tmx[rt]=1;
			sum[rt]=mn[rt]=mx[rt]=read(), smn[rt]=INF, smx[rt]=-INF;
			return;
		}
		Build(l,l+r>>1,ls), Build((l+r>>1)+1,r,rs);
		Update(rt);
	}
	void Modify_Add(int l,int r,int rt,int L,int R,int v)
	{
		if(L<=l && r<=R) {Add(rt,v); return;}
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m) Modify_Add(lson,L,R,v);
		if(m<R) Modify_Add(rson,L,R,v);
		Update(rt);
	}
	void Modify_Max(int l,int r,int rt,int L,int R,int v)
	{
		if(mn[rt]>=v) return;
		if(L<=l && r<=R && smn[rt]>v) {Max(rt,v); return;}
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m) Modify_Max(lson,L,R,v);
		if(m<R) Modify_Max(rson,L,R,v);
		Update(rt);
	}
	void Modify_Min(int l,int r,int rt,int L,int R,int v)
	{
		if(mx[rt]<=v) return;
		if(L<=l && r<=R && smx[rt]<v) {Min(rt,v); return;}
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m) Modify_Min(lson,L,R,v);
		if(m<R) Modify_Min(rson,L,R,v);
		Update(rt);
	}
	int Query_Max(int l,int r,int rt,int L,int R)
	{
		if(L<=l && r<=R) return mx[rt];
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m)
			if(m<R) return std::max(Query_Max(lson,L,R),Query_Max(rson,L,R));
			else return Query_Max(lson,L,R);
		else return Query_Max(rson,L,R);
	}
	int Query_Min(int l,int r,int rt,int L,int R)
	{
		if(L<=l && r<=R) return mn[rt];
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m)
			if(m<R) return std::min(Query_Min(lson,L,R),Query_Min(rson,L,R));
			else return Query_Min(lson,L,R);
		else return Query_Min(rson,L,R);
	}
	LL Query_Sum(int l,int r,int rt,int L,int R)
	{
		if(L<=l && r<=R) return sum[rt];
		PushDown(rt);
		int m=l+r>>1;
		if(L<=m)
			if(m<R) return Query_Sum(lson,L,R)+Query_Sum(rson,L,R);
			else return Query_Sum(lson,L,R);
		else return Query_Sum(rson,L,R);
	}
}T;

int main()
{
	#define S 1,n,1
	int n=read(); T.Build(S);
	for(int m=read(),opt,l,r; m--; )
	{
		opt=read(),l=read(),r=read();
		if(opt==1) T.Modify_Add(S,l,r,read());
		else if(opt==2) T.Modify_Max(S,l,r,read());
		else if(opt==3) T.Modify_Min(S,l,r,read());
		else if(opt==4) printf("%lld\n",T.Query_Sum(S,l,r));
		else if(opt==5) printf("%d\n",T.Query_Max(S,l,r));
		else printf("%d\n",T.Query_Min(S,l,r));
	}
	#undef S
	return 0;
}