EM算法之GMM聚类

以下为GMM聚类程序

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
data=pd.read_csv('Fremont.csv',index_col='Date',parse_dates=True)
print(data.head())

data.plot()
plt.show()
data.resample('w').sum().plot()#以周为时间统计

data.resample('D').sum().rolling(365).sum().plot()
plt.show()

##按照时间为统计
data.groupby(data.index.time).mean().plot()
plt.xticks(rotation=45)
plt.show()

data.columns=['West','East']
data['Total']=data['West']+data['East']
pivoted=data.pivot_table('Total',index=data.index.time,columns=data.index.date)
pivoted.iloc[:5,:5]
print(pivoted.iloc[:5,:5])
pivoted.plot(legend=False,alpha=0.01)
plt.xticks(rotation=45)
plt.show()

print(pivoted.shape)
X=pivoted.fillna(0).T.values
print(X.shape)

from sklearn.decomposition import PCA
X2 =PCA(2).fit_transform(X)
print(X2.shape)
plt.scatter(X2[:,0],X2[:,1])
plt.show()

from sklearn.mixture import GaussianMixture
gmm =GaussianMixture (2)
gmm.fit(X)
# labels= gmm.predict_proba(X)
# print(labels)
labels=gmm.predict(X)
print(labels)
plt.scatter(X2[:,0],X2[:,1],c=labels,cmap='rainbow')
plt.show()

from sklearn.datasets.samples_generator import make_blobs
X,y_true =make_blobs(n_samples=800,centers=4,random_state=11)
plt.scatter(X[:,0],X[:,1])
plt.show()

from sklearn.cluster import KMeans
KMeans =KMeans(n_clusters=4)
KMeans.fit(X)
y_Kmeans=KMeans.predict(X)
plt.scatter(X[:,0],X[:,1],c=y_Kmeans,s=50,cmap='viridis')
centers=KMeans.cluster_centers_
plt.show()

from sklearn.mixture import GaussianMixture
gmm =GaussianMixture(n_components=4).fit(X)
labels=gmm.predict(X)
print(labels)
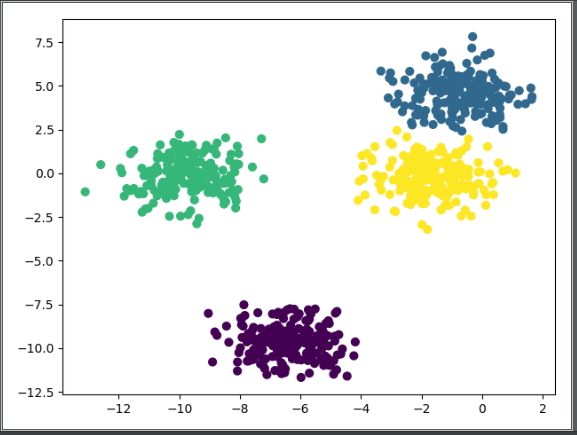
plt.scatter(X[:,0],X[:,1],c=labels,s=40,cmap='viridis')
plt.show()

　　

运行结果