密码学数论基础部分总结之 有限域GF(p) Galois Fields

　　今天花了一下午的时间学习密码学的数论部分，下面将学到的内容进行一下总结，也算是加深记忆。我本身对密码学这方面比较感兴趣，而且本节出现了许多数学公式，使用刚刚学习的LaTex公式来呈现出来，练习练习，何乐而不为。

　　首先给出了群，交换群（阿贝尔群），环，交换环，整环，域的定义，大致如下图所示：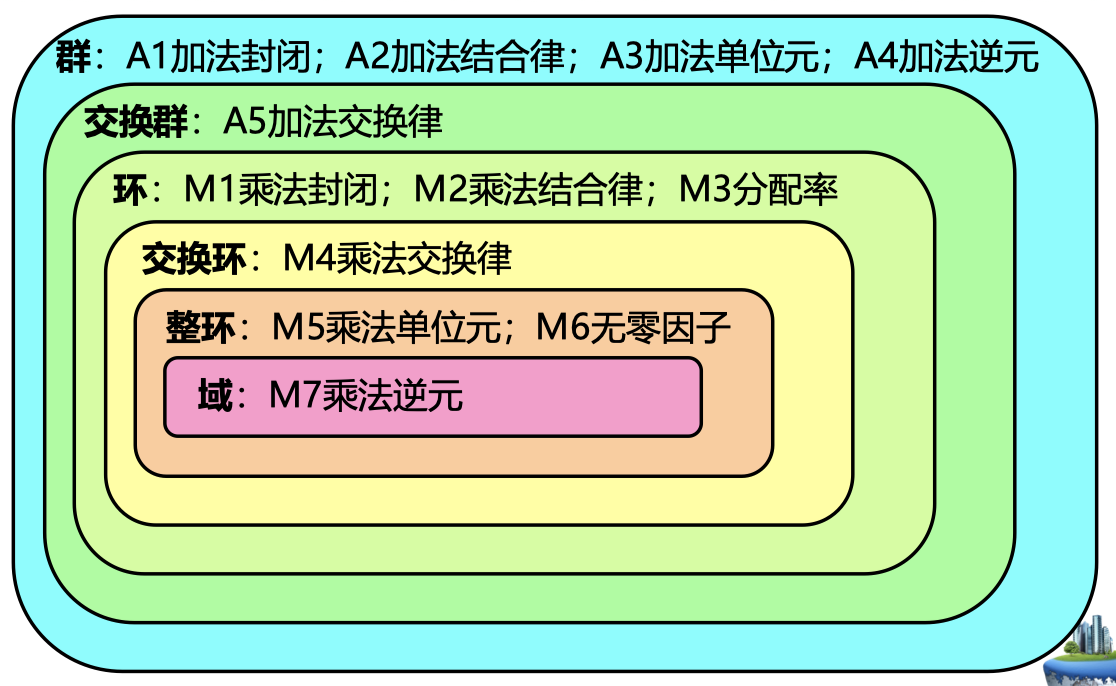

　　涉及到的第一个重要的新概念就是有限域$GF(p)$ Galois Fields

　　有限域的元素个数是一个素数的幂$p^n$，n为正整数，一般记为$GF(p^n)$，我们最为关注的只有两种情况：n=1即$GF(p)$；p为2即$GF(2^n)$。

　　$GF(p)$的空间是模p的完全剩余类$Z_p : \left\{0, 1, \cdots, p-1 \right\}$

　　$GF(2^n)$中的的元素是系数为二进制0和1的多项式，最高不超过n-1次。一个元素可以被表示成一个长度为n的位矢量。例如二进制数$11001_2$在$GF(2^5)$中可以记作$x^4+x^3+1$

　　这样来看，$GF(p)$和$GF(2^n)$域中的元素都可以用多项式来表示，一个多项式可以被表示成如下形式：$$f(x)=a_{n}x^n+a_{n-1}x^{n-1}+\cdots+a_{1}x+a_0=\sum^n_{i=0}a_{i}x^i$$

　　下面是重头戏，如何计算？针对三种不同的作用域我们定义了三种不同的多项式运算。

　　1.普通多项式运算。这个不必多说，从小学初中就开始学，就是我们认识的普通多项式。

　　2.系数在$Z_p$中的多项式运算。和普通多项式运算不同的是，系数要进行模p运算。模可以是任意素数，一般取二，是最简单的情况。例如:$$f(x)=x^3+x^2+1,\  \ g(x)=x^2+x+1\\f(x)+g(x)=x^3+x,\  \ f(x)\times g(x)=x^5+x+1$$

　　可见多项式的系数在运算的时候进行了模2处理。

　　3.有限域$GF(2^n)$上的多项式运算。这种运算和计算机的运作方式很相似，对于一个有限域$GF(2^n)$我们定义如下要求：系数对2取模运算，最高次数小于n，多项式对n次素多项式取模运算。既然是域那就有逆元，可以用拓展欧几里得算法求逆。

　　下面分别介绍在$GF(2^n)$上的四则运算：

　　1.加法（减法）

　　$GF(2^n)$上的加法即比特串的异或运算，因为是异或，加减其实是一样的，都是异或而已。$$(x^2+1)+(x^2+x+1)=x\\101_2\oplus 111_2=010_2$$

　　2.乘法

　　乘法即比特串的移位和异或运算。实际运算的时候和普通乘法很像，只不过加法变成了异或。下面的运算用了一个小技巧，异或的结果只和参与异或的1的个数有关，奇数则为1，偶数则为0。$$\ \ \ 101\\ \underline{\times011}\\ \ \ \ 101\\ \ \underline{1010}\\ \ 1111$$

　　或者可以表示为$011_2\times 101_2=(101_2)<<1\oplus (101_2)<<0=1111_2$其中<<为移位符。

　　3.取模

　　读者可能会好奇，为什么没有除法。这是因为在$GF(2^n)$上取模运算就相当于除法啦。多项式取模有一个简单的算法，重复用既约多项式剪掉最高次项。下面是一个极其简单的例子。$$(x^3+x^2+x+1)mod(x^3+x+1)=x^2\\1111_2mod1011_2=1111_2\oplus 1011_2=100_2$$

　　这个例子过于简单，如果用$(x^9+x^8+x^6+x^4+x^3+x^2+x+1)mod(x^4+x+1)$即$1101011111mod10011$有两种做法，一种是在被除数后面补上三个0（除数四位 4-1=3），然后像做除法一样除掉除数10011，如果最高位是1就添1，是零就直接写0，最后得到余数0010。还有一种等价做法就是用除数的最高位和被除数的最高位对齐。减（异或）一次，然后继续这个过程直到产生余数。