java第二次课件课后动手动脑习题整理总结（2019年9月23号）

一、动手动脑 1

1.题目

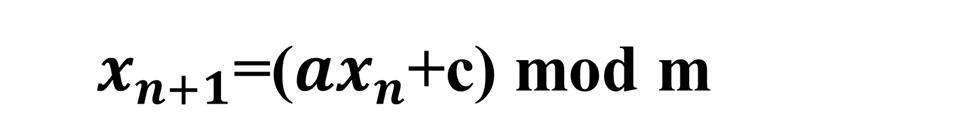
2.程序源代码

 package yang8;
 
 import java.util.Scanner;
 import java.util.Random;
 
 public class shengchengsuiji {
  public static void main(String[] args) {
      //实例化对象
      Random rand=new Random();
      Scanner input=new Scanner(System.in);
     System.out.println("请输入生成随机数的数量：");
     int num=input.nextInt();
     System.out.println("请输入每行打印随机数的数量：");
     int n=input.nextInt();
     int j=0;
     //随机生成一个0-100之间的种子
     int seed=rand.nextInt(99)+1;
     //循环num次
     for(int i=0;i<num;i++)
     {
         //用纯随机数生成器生成随机数
         seed=(16807*seed+0)%2147483647;
         j++;
         if(j%n==0) {
             System.out.println("\n");
         }
     System.out.print(seed+"\t");
     }
     System.out.println("\n");
     //输出提示信息
     System.out.println("生成完毕");
 }
 }

3.运行结果

二、动手动脑 2

1、题目

请看以下代码，你发现了有什么特殊之处吗？

 // MethodOverload.java
 // Using overloaded methods
 
 //***函数重载***
 public class MethodOverload {
 
     public static void main(String[] args) {
         System.out.println("The square of integer 7 is " + square(7));
         System.out.println("\nThe square of double 7.5 is " + square(7.5));
     }
 
     public static int square(int x) {
         return x * x;
     }
 
     public static double square(double y) {
         return y * y;
     }
 }

2.解答

发现：两个函数方法名相同，功能相同，但两个方法参数类型不同。

原因：这是java中的方法重载，方法重载的条件是值方法名相同，但方法的参数类型、参数个数、参数类型顺序不同中有一个或多个满足，

则称为方法重载。

三、课后实验

1.题目

查看一下JDK中System.out.println()方法，你发现了什么？

2.发现

JDK中有许多System.out.println()同名的重载方法。

3.原因

为了让编写代码时输出不同类型数据时更加方便，所以把输出的方法都用同名重载或方法重载。