BinaryTree(二叉树) - 再谈二叉树

　　经过两天的研究，总算是完全梳理清二叉树的基本操作了，然后我又发现了一些对二叉树的新的认识。

　　先具体说说删除操作，前面在对二叉树的补充中，我说到了二叉树的删除操作可以有两种不同的代码编写方式（可点这里去看一下），这点我还是这么认为，但在此基础上我又发现我对书上的理解还不够的地方：

　　用图来说明（删除图中节点65）：

　　按我的上一篇关于二叉树的删除操作的第二种说法对这种情况下进行删除操作，要删除65，要在65的右子树中找到一个恰比65小的节点是不可能的，所以肯定会直接删除65（因为65本身是最小的）；第一种说法则是先在65的右子树中找到恰比大的节点72，然后将72接到41右边，91整颗子树接到72的右边，再删除65。但书上对这种情况下的65进行删除时，并不寻找恰比65小的节点，也很意外的并不寻找恰比65大的节点，而是直接删除65，然后把91接到41右边就完成了，在这种情况下可以节省部分时间，但是也没有错，一样有O(1)的时间进行删除的情况出现，一样满足二叉树的基本要求——右孩子大于父节点，左孩子小于父节点。

　　按书上删除操作删除后的二叉树的样子：

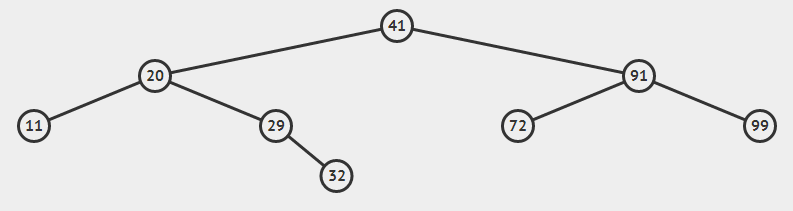
　　按我的第一种观点删除后的二叉树的样子：

　　然后我给出书上的删除操作的主要代码：

/*
 *    函数功能：参数2与参数3的替换
 *
 *    参数说明:
 *        1.接收一棵已存在的二叉树的根节点。
 *        2.要删除的节点。
 *        3.要删除的节点的右子节点或者恰比要删除节点大的节点
 *
 *    无返回值
 */
static void SubtreeChange(Tree * pRoot, Tree * delNode, Tree * delMaxChid)        //将要删除的节点替换为它的后继节点
{
    //如果要删除的节点的双亲为空说明节点为根节点，所以将根节点的右子树中的某节点换到根节点的位置
    if(delNode -> parent == NULL)
        pRoot = delMaxChid;

    //如果要删除的节点是它父节点的左孩子，则将要删除的节点的右子树中的某节点换到要删除的节点的位置
    else if(delNode == delNode -> parent -> left)
        delNode -> parent -> left = delMaxChid;

    //否则要删除的节点不是他父节点的左孩子，则把要删除的节点的右子树中的某节点换到要删除的节点的位置
    else
        delNode -> parent -> right = delMaxChid;

    //右子树中的某节点不为空，则将它的双亲改为要删除节点的双亲
    if(delMaxChid != NULL)
        delMaxChid -> parent = delNode -> parent;
}

/*
 *    函数功能:删除节点
 *
 *    参数说明:
 *        1.接收一棵已存在的二叉树的根节点。
 *        2.接收要删除的节点。
 *
 *    返回值：二叉树的根节点
 */
static Tree * DeleteNode(Tree * pRoot, Tree * delNode)
{
    Tree * tempNode;

    //case 1:要删除的节点无左孩子，调用函数SubtreeChange()来将要删除节点的右孩子的位置换到删除节点的位置上
    if(delNode -> left == NULL)
        SubtreeChange(pRoot, delNode, delNode -> right);

    //case 2:要删除的节点无右孩子，调用函数SubtreeChange()来将要删除节点的左孩子的位置换到删除节点的位置上
    else if(delNode -> right == NULL)
        SubtreeChange(pRoot, delNode, delNode -> left);

    /*
     * case 3:要删除的节点有两个孩子，先调用函数FinMinMax()找到恰比删除节点大的节点，
     * 然后如果找到的这个节点的父节点不是要删除的节点，则调用SubtreeChange()来替换找
     * 到的节点和它的右孩子的位置，然后再调用一次SubtreeChange()来替换要删除的节点和
     * 恰比删除节点大的位置
     * 如果找到的节点的父节点是删除节点就直接调用函数SubtreeChange()来替换删除节点和
     * 恰比删除节点大的位置
     */
    else
    {
        tempNode = FindMinMax(delNode -> right);
        if(tempNode -> parent != delNode)
        {
            SubtreeChange(pRoot, tempNode, tempNode -> right);
            tempNode -> right = delNode -> right;
            tempNode -> right -> parent = tempNode;
        }
        SubtreeChange(pRoot, delNode, tempNode);
        tempNode -> left = delNode -> left;
        tempNode -> left -> parent = tempNode;
    }

    free(delNode);
    return pRoot;
}

　　代码是看《算法导论》中给出的伪代码来实现的，当然编写方式肯定不止这一种，如我上面提到的应该依据个人的理解来编写不同的代码实现相同的功能，我想这才算是自己真正的理解了的成果。。。

　　下面，我从创建一个二叉树开始解析可能会遇到的问题和我个人刚开始不是很理解的地方。

　　　一.二叉树的创建有两种情况，一种是一开始没有一组数，在添加节点过程中慢慢创建，二是一开始就有一组数据需要用二叉树结构来生成。

　　　　1.先初始化一个二叉树结构的根：

Tree * initBinaryTree(void)        //初始化二叉树
{
    Tree * root = NULL;

    return root;
}

　　　　之后再调用插入节点函数，慢慢生成一个二叉树：

static Tree * NewNode(Tree * pRoot, ElemType X)        //申请新节点
{
    Tree * tempNode;

    tempNode = (Tree *)malloc(sizeof(Tree));
    tempNode -> val = X;
    tempNode -> parent = tempNode -> left = tempNode -> right = NULL;

    return tempNode;
}

static Tree * NodeInsertPos(Tree * pRoot, Tree * newNodePos)        //找到新节点插入的位置并插入树中
{
    Tree * p = NULL, * q;

    q = pRoot;

    while(q != NULL)
    {
        p = q;
        if(newNodePos -> val < q -> val)
            q = q -> left;
        else if(newNodePos -> val > q -> val)
            q = q -> right;
        else　　　　　　　　//如果插入的数据存在
            break;
    }

    newNodePos -> parent = p;
    if(p == NULL)
        pRoot = newNodePos;
    else if(newNodePos -> val < p -> val)
        p -> left = newNodePos;
    else
        p -> right = newNodePos;

    return pRoot;
}

　　　　相信都能看懂添加操作的实现。这里添加的操作可以试试用递归实现一次。

　　　　2.有两个方法，一是用一种叫做：扩展先序遍历序列的方式创建（递归实现），二是用普通的循环来实现，如果不理解递归的话就很难理解递归创建的原因。

　　　　　　①.递归创建二叉树代码：

Tree * CreateBiTree(void)
{
    Tree * T;
    ElemType X;

    scanf("%d", &X);
    if(X == 0)
        T = NULL;
    else
    {
        T = (tree *)malloc(sizeof(tree));
        T -> DATA = X;
        T -> left = CreateBiTree();
        T -> right = CreateBiTree();
    }
    return T;
}

　　　　　　它的输入是有讲究的，具体参见上面给的链接。

　　　　　　②.(1)循环创建二叉树代码(我直接用for循环调用插入节点函数，和慢慢插入的没什么区别)：

Tree * Cycle_CreateBiTree(int Num) {

    Tree * root = NULL, * tempNode;
    int i, val;

    scanf("%d", &val);
    root = InsertNode(root, val);
    for(i = 1; i < Num; i++)
    {
        scanf("%d", &val);
        tempNode = InsertNode(root, val);
    }

    return root;
}

　　　　　　　(2)想了一下，觉得调用插入函数的方法还是不够满意，改了一下（数据可以重复添加）：

Tree * Cycle_CreateBiTree(int Num) {

    Tree * root, * tempNode, * nextNode, * contNode;
    int i;

    root = (Tree *)malloc(sizeof(Tree));
    tempNode = root;
    scanf("%d", &tempNode -> val);
    tempNode -> parent = tempNode -> left = tempNode -> right = NULL;

    for(i = 1; i < Num; i++)
    {
        nextNode = (Tree *)malloc(sizeof(Tree));
        scanf("%d", &nextNode -> val);
        nextNode -> parent = tempNode;
        nextNode -> left = nextNode -> right = NULL;
        contNode = root;
　　　　　while(contNode != NULL)
        {
            tempNode = contNode;
            if(nextNode -> val < contNode -> val)
                contNode = contNode -> left;
            else
                contNode = contNode -> right;
        }
        if(nextNode -> val < tempNode -> val)
            tempNode -> left = nextNode;
        else
            tempNode -> right = nextNode;
        tempNode = nextNode;
    }

    return root;
}

　　　二.二叉树的遍历：前序、中序和后序遍历。

　　　　主要是递归遍历的理解：刚开始我只能理解函数调用自身里面只有一个调用，例如：

void Function (int i)
{
     Function(i);
}

　　　　当看到里面有两个时就有点懵了：

void TraverseBiTree(Tree * pRoot)
{
    if(pRoot != NULL)
    {
        printf("%d ", pRoot -> val);
        TraverseBiTree(pRoot -> left);
        TraverseBiTree(pRoot -> right);
    }
}

　　　　现在终于不会懵了，解释一下(以上面这段代码为例)：当第一次进入递归时pRoot -> left进去后负责自己这一边（也就是左子树），各种遍历，其中还会有一些pRoot -> right，然后就产生了许多层的子递归，但每层递归至多两个子递归...而第一次的pRoot -> right则负责右子树中的所有遍历，其中也还有一些pRoot -> left，也会产生许多子递归，与pRoot -> left一样，这样才能保证二叉树的所有节点都不会被忽略掉。然后为什么前、中、后序遍历的代码只是位置前后的不同就出现了不同的输出方式呢，特别是中序，可以按从小到大来排序，这个可以在大脑里模仿一下我所描述的进入递归后函数的行为...具体还真不好解释。总之，前、中、后序遍历的代码很简单，我就只简单的贴个前序的吧。

　　　三.理解了递归就可以理解二叉树中的很多操作了...如计算二叉树的深度、度等，虽然也可以用循环来实现，但递归看起来比较简洁。

int GetDepth(Tree * pRoot)                //二叉树的深度
{
    int xL, yR;

    if(pRoot == NULL)
        return 0;
    xL = GetDepth(pRoot -> left);
    yR = GetDepth(pRoot -> right);
    return (xL > yR ? xL + 1 : yR + 1);
}

int GetDegree(Tree * pRoot)                //二叉树的度
{
    if(pRoot == NULL)
        return 0;
    return GetDegree(pRoot -> left) + GetDegree(pRoot -> right) + 1;
}

　　　四.二叉树的插入操作，插入操作是二叉树中除删除操作外较难的一个操作，但我认为难度真的差删除很多...唉...总之，先看插入操作的代码（和前面的一段插入的一样）：

static Tree * NewNode(Tree * pRoot, ElemType X)        //申请新节点
{
    Tree * tempNode;

    tempNode = (Tree *)malloc(sizeof(Tree));
    tempNode -> val = X;
    tempNode -> parent = tempNode -> left = tempNode -> right = NULL;

    return tempNode;
}

static Tree * NodeInsertPos(Tree * pRoot, Tree * newNode)        //找到新节点插入的位置并插入树中
{
    Tree * p = NULL, * q;

    q = pRoot;

    while(q != NULL)
    {
        p = q;
        if(newNode -> val < q -> val)
            q = q -> left;
        else if(newNode -> val > q -> val)
            q = q -> right;
        else
            break;
    }

    newNodePos -> parent = p;
    if(p == NULL)
        pRoot = newNode;
    else if(newNode -> val < p -> val)
        p -> left = newNode;
    else if(newNode -> val > p -> val)
        p -> right = newNode;

    return pRoot;
}

　　　　具体解释一下第二段，第一段只是申请一个节点，没什么难度，第二段代码要更复杂点。先解释一下函数的参数：

/*
 *    函数功能:找到新节点插入的位置并插入书中
 *
 *    参数说明:
 *        1.接收一个已存在的二叉树。
 *        2.接收一个带有数据的新节点
 *
 *    返回值:二叉树的根
 */

　　　　然后来看代码:

      Tree * p = NULL, * q;

      q = pRoot;

      while(q != NULL)
      {
          p = q;
          if(newNode -> val < q -> val)
              q = q -> left;
         else if(newNode -> val > q -> val)
             q = q -> right;
         else
             break;
     }

　　　　为了保证不影响到二叉树的根节点，所以定义了p,q指针，运用循环比较，找到一个新节点合适的位置（合适的位置也就是说，找到新节点的父节点的位置，当然，目前新节点的父节点的孩子肯定是NIL的，所以，找到合适的位置后需要给他们之间建立一个关系），然后就出现了：

    //这里就是给新节点找双亲的操作
    newNodePos -> parent = p;

    //如果p是NIL，新节点没有双亲，将新节点设置为根节点
    if(p == NULL)
        pRoot = newNodePos;

    //如果新节点的值小于它的双亲的值，那新节点就是它双亲的左孩子了
    else if(newNodePos -> val < p -> val)
        p -> left = newNodePos;

    //反之就是右孩子
    else if(newNodePos -> val > p -> val)
        p -> right = newNodePos;

　　　五.查找。关于查找，我说一下二叉树查找的时间复杂度吧，因为二叉树的性质，所以应用递归（也可以用循环）进行查找很合适，每次递归就进行比较判断，节省了很多的时间，对于一个输入规模为n的满二叉树，它的查找最坏时间复杂度为O(lgn)。也就是它的深度，为什么是O(lgn)呢，因为它的查找就是二分查找的算法，可以简略的证明，二分查找的最坏时间复杂度：

T(1) = 1　　　　　　　 N = 1;
T(N) = T(N/2) + c      N > 1;        //我们要找的数据在中间的往左或右移变量 c 的位置

T(N) = T(N/2) + c
     = T(N/4) + 2c
     = T(N/8) + 4c
        ...
     = T(N/k) + (k/2)c

其中 [N/k] = 1 时有 k = 2[lgN] ~ (N)（相当于把T(N/2) + c 的位置交换为c + T(N/2) = T(1) + (N/2)c）

当 [N/k] = 1 时, 即 N/2[lgN] = 1, 有 T(N/k) = T(1)
其中[]表示向下取整。

综合上述有：
   T(N) =  T(1) + lgNc = (lgN + 1)c = O(lgN)

　　完整的二叉树代码：

#include<stdio.h>
#include<stdlib.h>
#include<conio.h>

typedef int ElemType;

typedef struct tree {
    ElemType val;            //节点数据
    struct tree * left;        //左孩子
    struct tree * right;    //右孩子
    struct tree * parent;    //双亲
}Tree;

Tree * initBinaryTree();
Tree * FindNode();
int GetDepth();
int GetDegree();
void TraverseBiTree();
Tree * FindBinaryNode();
static Tree * NewNode();
static Tree * NodeInsertPos();
Tree * InsertBiTree();
static Tree * FindMin();
static Tree * FindMax();
static void SubtreeChange();
static Tree * DeleteNode();
Tree * removeNode();
void DeleteTree();

Tree * initBinaryTree(void)        //初始化二叉树
{
    Tree * root = NULL;
    return root;
}

Tree * FindNode(Tree * pRoot, ElemType X)        //查找节点数据
{
    if(pRoot == NULL)        //如果二叉树为空或二叉树中没找到相同数据的节点
    {
        fprintf(stderr, "Inexistence!\n");
        return NULL;
    }

    if(X < pRoot->val)
        return FindNode(pRoot->left, X);
    else if(X > pRoot->val)
        return FindNode(pRoot->right, X);
    else        //相同
        return pRoot;
}

int GetDepth(Tree * pRoot)                    //二叉树的深度
{
    int xL, yR;
    if(pRoot == NULL)
        return 0;
    xL = GetDepth(pRoot->left);
    yR = GetDepth(pRoot->right);
    return (xL > yR ? xL + 1 : yR + 1);
}

int GetDegree(Tree * pRoot)                //二叉树的度
{
    if(pRoot == NULL)
        return 0;
    return GetDegree(pRoot->left) + GetDegree(pRoot->right) + 1;
}

void TraverseBiTree(Tree * pRoot)
{
    if(pRoot != NULL)
    {
        TraverseBiTree(pRoot->left);
        printf("%d ", pRoot->val);
        TraverseBiTree(pRoot->right);
    }
}

static Tree * NewNode(Tree * pRoot, ElemType X)        //申请新节点
{
    Tree * tempNode;

    tempNode = (Tree *)malloc(sizeof(Tree));
    tempNode->val = X;
    tempNode->parent = tempNode->left = tempNode->right = NULL;

    return tempNode;
}

/*
 *    函数功能:
 *
 *    参数说明:
 *        1.接收一个已存在的二叉树。
 *        2.接收一个新节点
 *
 *    返回值:二叉树的根
 */
static Tree * NodeInsertPos(Tree * pRoot, Tree * newNode)        //找到新节点插入的位置并插入树中
{
    Tree * p = NULL, * q;

    q = pRoot;

    while(q != NULL)
    {
        p = q;
        if(newNode->val < q->val)
            q = q->left;
        else if(newNode->val > q->val)
            q = q->right;
        else
            break;
    }

    //前面的循环给新节点找到了父节点
    newNode->parent = p;

    //如果p是NIL，新节点没有双亲，则设置新节点为根节点
    if(p == NULL)
        pRoot = newNode;

    //如果新节点的值小于它的双亲的值，那新节点就是它双亲的左孩子了
    else if(newNode->val < p->val)
        p->left = newNode;

    //反之就是右孩子
    else
        p->right = newNode;

    return pRoot;
}

Tree * InsertBiTree(Tree * pRoot, ElemType X)                //将新节点插入二叉树
{
    Tree * newNode;

    if((newNode = NewNode(pRoot, X)) == NULL)
        return pRoot;

    return NodeInsertPos(pRoot, newNode);
}

static Tree * FindMin(Tree * findNode)            //找最小值。此处用来找到一个节点数据恰好比当前节点数据大的节点
{
    if(findNode == NULL)
        return NULL;
    else if(findNode->left == NULL)
        return findNode;
    else
        return FindMin(findNode->left);
}

static Tree * FindMax(Tree * findNode)            //找最大值。此处用来找到一个节点数据恰好比当前节点数据大的节点
{
    if(findNode == NULL)
        return NULL;
    else if(findNode->right == NULL)
        return findNode;
    else
        return FindMax(findNode->right);
}

/*
 *    函数功能：参数2与参数3的替换
 *
 *    参数说明:
 *        1.接收一棵已存在的二叉树的根节点。
 *        2.要删除的节点。
 *        3.要删除的节点的右子节点或者恰比要删除节点大的节点
 *
 *    返回值：空
 */
static void SubtreeChange(Tree * pRoot, Tree * delNode, Tree * delMaxChid)        //将要删除的节点替换为它的后继节点
{
    //如果要删除的节点的双亲为空说明节点为根节点，所以将根节点的右子树中的某节点换到根节点的位置
    if(delNode->parent == NULL)
        pRoot = delMaxChid;

    //如果要删除的节点是它父节点的左孩子，则将要删除的节点的右子树中的某节点换到要删除的节点的位置
    else if(delNode == delNode->parent->left)
        delNode->parent->left = delMaxChid;

    //否则要删除的节点不是他父节点的左孩子，则把要删除的节点的右子树中的某节点换到要删除的节点的位置
    else
        delNode->parent->right = delMaxChid;

    //右子树中的某节点不为空，则将它的双亲改为要删除节点的双亲
    if(delMaxChid != NULL)
        delMaxChid->parent = delNode->parent;
}

/*
 *    函数功能:删除节点
 *
 *    参数说明:
 *        1.接收一棵已存在的二叉树的根节点。
 *      2.接收要删除的节点。
 *
 *    返回值：二叉树的根节点
 */
static Tree * DeleteNode(Tree * pRoot, Tree * delNode)
{
    Tree * tempNode;

    //case 1:要删除的节点无左孩子，调用函数SubtreeChange()来将要删除节点的右孩子的位置换到删除节点的位置上
    if(delNode->left == NULL)
        SubtreeChange(pRoot, delNode, delNode->right);

    //case 2:要删除的节点无右孩子，调用函数SubtreeChange()来将要删除节点的左孩子的位置换到删除节点的位置上
    else if(delNode->right == NULL)
        SubtreeChange(pRoot, delNode, delNode->left);

    /*
     * case 3:要删除的节点有两个孩子，先调用函数FinMin()找到恰比删除节点大的节点，
     * 然后如果找到的这个节点的父节点不是要删除的节点，则调用SubtreeChange()来替换找
     * 到的节点和它的右孩子的位置，然后再调用一次SubtreeChange()来替换要删除的节点和
     * 恰比删除节点大的位置
     * 如果找到的节点的父节点是删除节点就直接调用函数SubtreeChange()来替换删除节点和
     * 恰比删除节点大的位置
     */
    else
    {
        tempNode = FindMin(delNode->right);
        if(tempNode->parent != delNode)
        {
            SubtreeChange(pRoot, tempNode, tempNode->right);
            tempNode->right = delNode->right;
            tempNode->right->parent = tempNode;
        }
        SubtreeChange(pRoot, delNode, tempNode);
        tempNode->left = delNode->left;
        tempNode->left->parent = tempNode;
    }

    free(delNode);
    return pRoot;
}

Tree * removeNode(Tree * pRoot, ElemType X)
{
    Tree * delNode;

    if((delNode = FindNode(pRoot, X)) == NULL)        //找到要删除的节点
        return pRoot;
    return DeleteNode(pRoot, delNode);                        //将其删除
}

void DeleteTree(Tree * pRoot)
{
    if(pRoot != NULL)
    {
        Deltree(pRoot->left);
        Deltree(pRoot->right);
        free(pRoot);
    }
    pRoot = initBinaryTree();
}

int main(void)
{
    ElemType data;
    Tree * h;
    char c;

    h = initBinaryTree();

    puts("1) 添加          2) 查找");
    puts("3) 深度、度    4) 查看");
    puts("5) 删除          q) Exit");
    while((c = getch()) != 'q')
    {
        switch(c)
        {
            case '1' :
                        printf("\n添加:");
                        scanf("%d", &data);
                        h = InsertBiTree(h, data);
                    break;
            case '2' :
                        printf("\n查找:");
                        scanf("%d", &data);
                        if(FindNode(h, data))
                        {
                            if(FindNode(h, data)->parent != NULL)
                                printf("您查找的数据的双亲为 %d\n", FindNode(h, data)->parent->val);
                            else
                                printf("null");
                        }
                    break;
            case '3' :
                        printf("\n二叉树的深度、度:%5d%5d\n", GetDepth(h), GetDegree(h));
                    break;
            case '4' :
                        printf("\n显示数据:\n");
                        TraverseBiTree(h);
                    break;
            case '5' :
                        printf("\n删除节点:");
                        scanf("%d", &data);
                        removeNode(h, data);
                    break;
        }
    }
    DeleteTree(h);
    return 0;
}

　　最后，这篇总结就到这里了，也不算太全面，学习能力有限，还有许多认识不足的地方和错误，还恳请看客不吝指正。