SAGE|DNA微阵列|RNA-seq|lncRNA|scripture|tophat|cufflinks|NONCODE|MA|LOWESS|qualitile归一化|permutation test|SAM|FDR|The Bonferroni|Tukey's|BH|FWER|Holm's step-down|q-value|

生物信息学-基因表达分析

为了丰富中心法则，研究人员使用不断更新的技术研究lncRNA的方方面面，其中技术主要是生物学上的微阵列芯片技术和表达数据分析方法，方方面面是指lncRNA的位置特征。

Background：根据中心法则，发现DNA与RNA与protein之间的关系，此时认为找到的RNA全部用于编码protein，但是实验结果中：非编码RNA含量高，而coding区只占很少的一部分。研究非编码RNA，发现noncoding与protein expression有关，所以总思路变成了研究noncoding区从而丰富中心法则，而研究noncoding区的前提是转录组分析。

转录组研究

1.依据实际研究的问题，可以有不同的思路

时间（生长发育不同阶段）特异性

空间（身体不同区域）特异性

Normal 与否

1. 随着测序技术的发展，出现了以下RNA的测序手段

SAGE：将RNA反转录得到的cDNA打碎，利用sanger测序法得到最后的序列

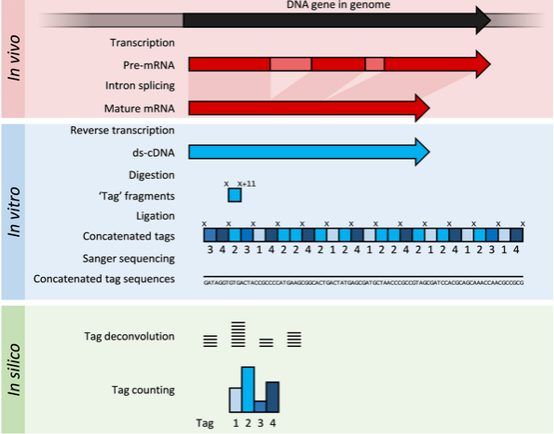
DNA微阵列： 将RNA打碎，用基于reference的探针（特指基因芯片）测得序列，此方法灵敏性高

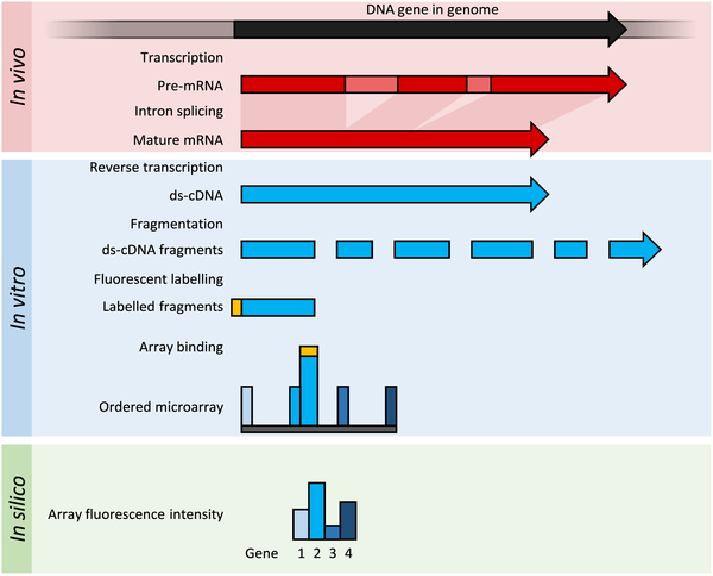
RNA-seq：将RNA打碎，再将片段RNA反转录cDNA，利用二代测序（short reads）assembly而成。

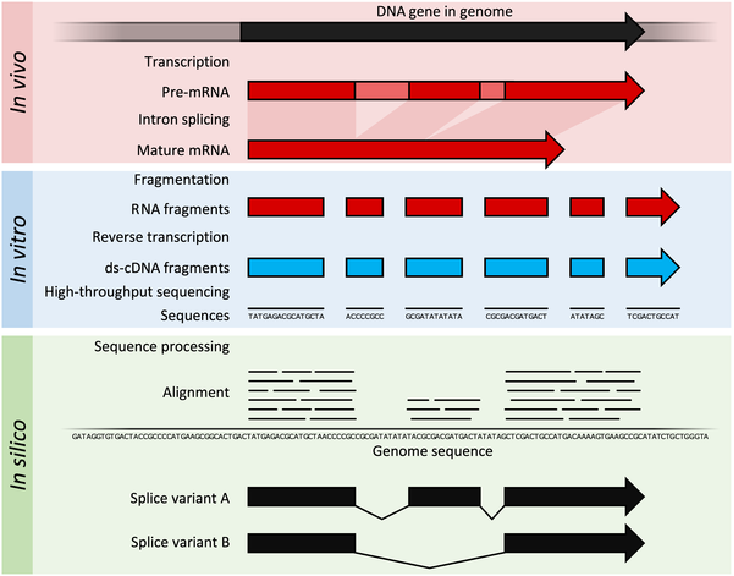
Long noncoding RNA

定义：

1.因为200bp，所以long；

2.因为No protein produce但同时有与coding gene具有相似结构（都有intro和exon），所以lncRNA长期被认为是假基因，直到发现其和转录调控有关系，才开始被重视。

起源：

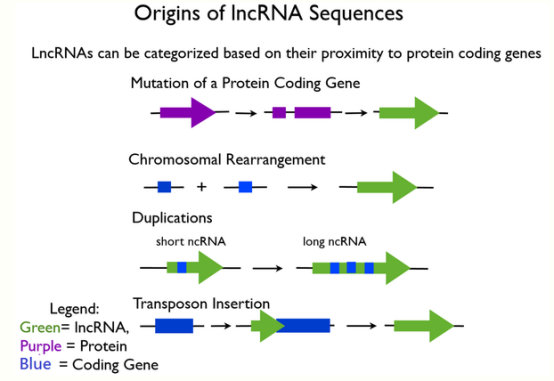
1. coding gene mutation变成noncoding gene，所以无法coding protein
2. Chromosome重组
3. sncRNA加倍成为lncRNA
4. sncRNA插入coding gene使之丧失功能但长度变长，成为lncRNA

分类：基于与protein的位置

lncRNA发现历史：

在大规模测序出现之前，只能利用sanger发现单个lncRNA。在完成human genome 之后，基于该数据库，得到的芯片，大大加速了lncRNA的发现。随着二代测序的大规模使用，大量发现结构，因此诞生了基于不同算法的assembly&annotation软件（eg，scripture、tophat、cufflinks）。所以，如今的思路是利用不同工具处理相同数据，将得到的不同结果集成为更准确的genome，从而得到比较可靠的reference。（review：Rinn and Chang，2012）但是2015用更多的原始数据用同样方法重做，发现其中有79%之前没有的，这是因为原始数据采集更在时间和空间上更为细致了。如今，得到了NONCODE （数量最多dataset）、MITranscript （最新）等各有侧重的数据库。

Assembly比对方式：

1.交叉--保留

2,存在不交叉的，利用其它参数信息（eg，位置信息）筛选

Gene expression 分析：

原则：重复&随机&间隔

Replication：biology（eg，同一个gene测100次得到100个sequence信息） &technical（对于100个sequence信息，可以随机抽取其中的任意N个，这种抽取做M次），这都是为了数据能更好的反应客观事实。

Randomization：无论是抽选或是物理设备参数设定，都要保证随机性。

Blocking：生物学实验的连贯性（物理条件一致，eg，一天一个完整实验，而不是一天所有完整实验中的一个步骤）

以微阵列方法为例的流程：

在仪器上得到荧光信号，将这些应该信号按照光的亮度赋值，由图转变为表，该表就是表达谱。根据荧光信号的特点，比如中间较强周围较弱就比较好，进行质量控制，也就是筛选质量较好的sample。此时，所有gene的表达量都在一个表格里面，其中使用三张芯片就被叫做生物学重复，以此创造：

	芯片1	芯片2	芯片3
Gene1	2	4	4
Gene2	5	4	14
Gene3	4	6	8

可知芯片1比芯片3的光照程度整体普遍弱，这可能是由于物理因素造成的。为了进行比较，要将其数值进行归一化（normalization），依据比价对象的不同，可将方法分为两种：

1. Intra：eg，芯片1内部比较不同gene表达量（技术是双通道的MA，归一化方法是LOWESS ）
2. Inter：eg，gene1在不同芯片上的表达量，（技术是单通道；思路可以是中位数归一化或qualitile归一化图

其中，qualitile归一化 的过程是：

	芯片1	芯片2	芯片3
Gene1	2	4	4
Gene2	5	4	14
Gene3	4	6	8

不看属于哪个gene，在芯片内部进行排序：

	芯片1	芯片2	芯片3
Mean=10/3	2（Gene1）	4（Gene1）	4（Gene1）
Mean=16/3	4（Gene3）	4（Gene2）	8（Gene3）
Mean=25/3	5（Gene2）	6（Gene3）	14（Gene2）

求均值并写回去，这样做是为了避免物理错误，物理错误会导致整张芯片的效果都不好。不用考虑排序会因为表达量一致而造成误差，因为实际上不存在表达量完全一致的情况：

	芯片1	芯片2	芯片3
Gene1	10/3	10/3	10/3
Gene2	25/3	16/3	25/3
Gene3	16/3	25/3	16/3

归一化之后，利用假设检验证明实际问题。

当数据服从某种分布（既有参数）时，可就某些参数（eg，mean）进行假设检验

当数据未知分布（即无参数），则采用permutation test：

使用的理论是t检验中的SAM，因为t-test需要有参数，但是现在数据未知参数，所以加入置换测试的方法

SAM"Statistical Analysis of Microarrays" specifically designed for microarray data analysis. It relies on the non-parametric permutation test. SAM is a variant of the t-test. Shown below is an excerpt of Tushner's paper describing the SAM algorithm:

Eg，分为测试组（treatment）和对照组（control）：下图是它们的数据分布D

Key	T1	T2	T3	C1	C2	C3
Gene1	1	2	3	4	5	6

将其随机打乱成1000个类似于下方表格的sample：

比如其中的2个是：

Key	T1	T2	T3	C1	C2	C3	Mean of T	Mean of C	STDEV of all
Gene1	6	1	2	3	4	5	3	4	1.870828693
Key	T1	T2	T3	C1	C2	C3	Mean of T	Mean of C	STDEV of all
Gene1	5	1	2	3	4	6	2.666666667	4.333333333	1.870828693

其中，S0是给定值，d可以认为是改良版的t值，如此得到1000个t值，这1000个t值可构成正态分布统计图表，最后根据总体分布，找到数据分布D的p值，而后根据该p值判断假设检验的结果。

由此，可以得到所有基因对应的p值，但是因为p值的错误率很高，所以需要采用多重假设检验对p值做检查。

可采用FDR

首先对于每个基因来说，都有p值，p值的含义是false positive rate(FPR，假正率)：q值是false discovery rate (FDR)：

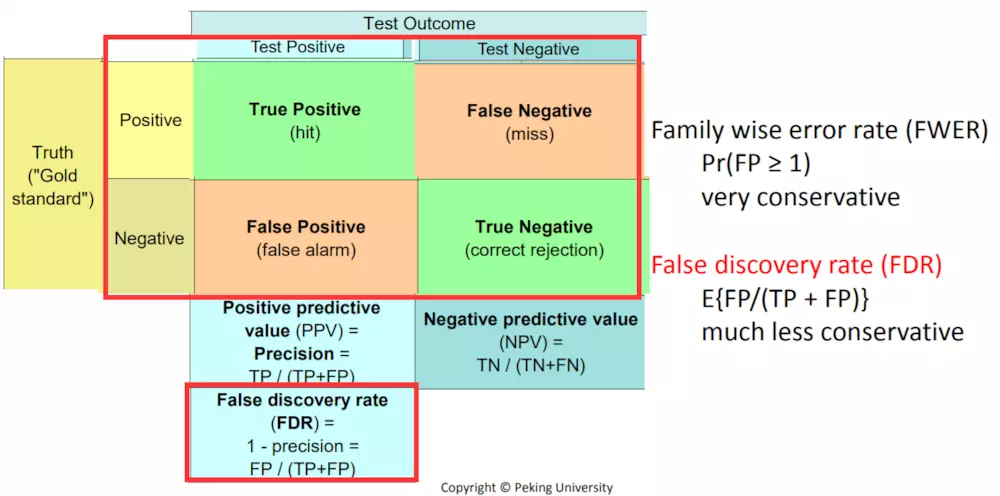
因为未知真实情况，但是从上图可知真实情况和估算情况之间的关系，所以可以使用别的方法计算FWER和FDR。

Control of FWER：

The Bonferroni procedure

Tukey's procedure

Holm's step-down procedure

Control of FDR

Benjamini–Hochberg procedure

Benjamini–Hochberg–Yekutieli procedure

例如，BH：

,

 ，所以q-value的期望即是FDR，所以，求出每个gene的q-value即可

原先每个gene都有自己的p值：

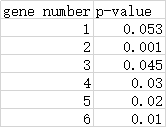
可靠gene的p值满足：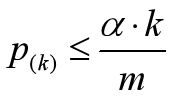

可靠gene的q值满足：

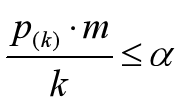
其中，k是gene number号，a是自己设定的0.05，m是所有gene个数,在这里是6；

把gene按照p值排序并据公式处理，得到：

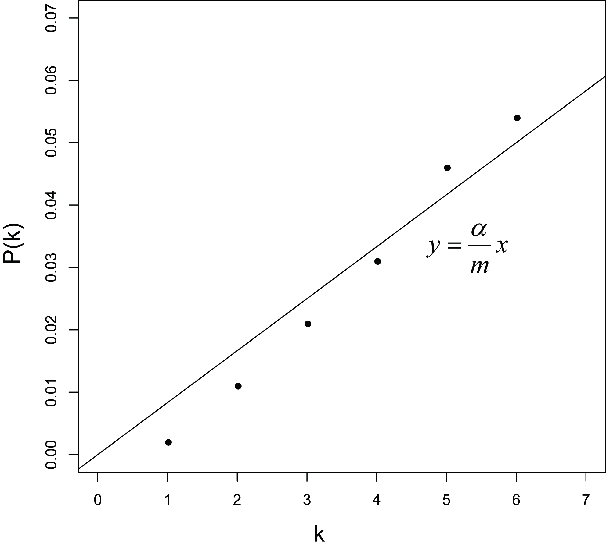
若写为函数表达则可得到上图，有四个gene的p值是可靠的。

http://compbio.pbworks.com/w/page/16252887/Differential%20Gene%20Expression%20and%20Hypothesis%20Testing