从卷积拆分和分组的角度看CNN模型的演化

博客：博客园 | CSDN | blog

写在前面

如题，这篇文章将尝试从卷积拆分的角度看一看各种经典CNN backbone网络module是如何演进的，为了视角的统一，仅分析单条路径上的卷积形式。

形式化

方便起见，对常规卷积操作，做如下定义，

• \(I\)：输入尺寸，长\(H\) 宽\(W\) ，令长宽相同，即\(I = H = W\)
• \(M\)：输入channel数，可以看成是tensor的高
• \(K\)：卷积核尺寸\(K \times K\)，channel数与输入channel数相同，为\(M\)
• \(N\)：卷积核个数
• \(F\)：卷积得到的feature map尺寸\(F \times F\)，channel数与卷积核个数相同，为\(N\)

所以，输入为\(M \times I \times I\)的tensor，卷积核为\(N \times M \times K \times K\)的tensor，feature map为\(N \times F \times F\)的tensor，所以常规卷积的计算量为

\[FLOPS = K \times K \times M \times N \times F \times F
\]

特别地，如果仅考虑SAME padding且\(stride = 1\)的情况，则\(F = I\)，则计算量等价为

\[FLOPS = K \times K \times M \times N \times I \times I
\]

可以看成是\((K \times K \times M) \times (N \times I \times I)\)，前一个括号为卷积中一次内积运算的计算量，后一个括号为需要多少次内积运算。

参数量为

\[\#Params = N \times M \times K \times K
\]

网络演化

总览SqueezeNet、MobileNet V1 V2、ShuffleNet等各种轻量化网络，可以看成对卷积核\(M \times K \times K\) 进行了各种拆分或分组（同时引入激活函数），这些拆分和分组通常会减少参数量和计算量，这就为进一步增加卷积核数量\(N\)让出了空间，同时这种结构上的变化也是一种正则，通过上述变化来获得性能和计算量之间的平衡。

这些变化，从整体上看，相当于对原始\(FLOPS = K \times K \times M \times N \times I \times I\)做了各种变换。

下面就从这个视角进行一下疏理，简洁起见，只列出其中发生改变的因子项，

• Group Convolution（AlexNet），对输入进行分组，卷积核数量不变，但channel数减少，相当于

  \[M \rightarrow \frac{M}{G}
  \]

  

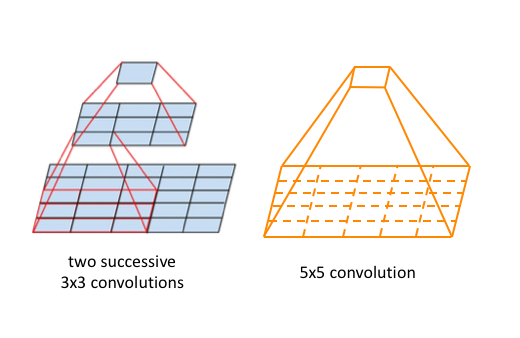
• 大卷积核替换为多个堆叠的小核（VGG），比如\(5\times 5\)替换为2个\(3\times 3\)，\(7\times 7\)替换为3个\(3\times 3\)，保持感受野不变的同时，减少参数量和计算量，相当于把 大数乘积 变成 小数乘积之和，

  \[(K \times K) \rightarrow (k \times k + \dots + k \times k)
  \]

  

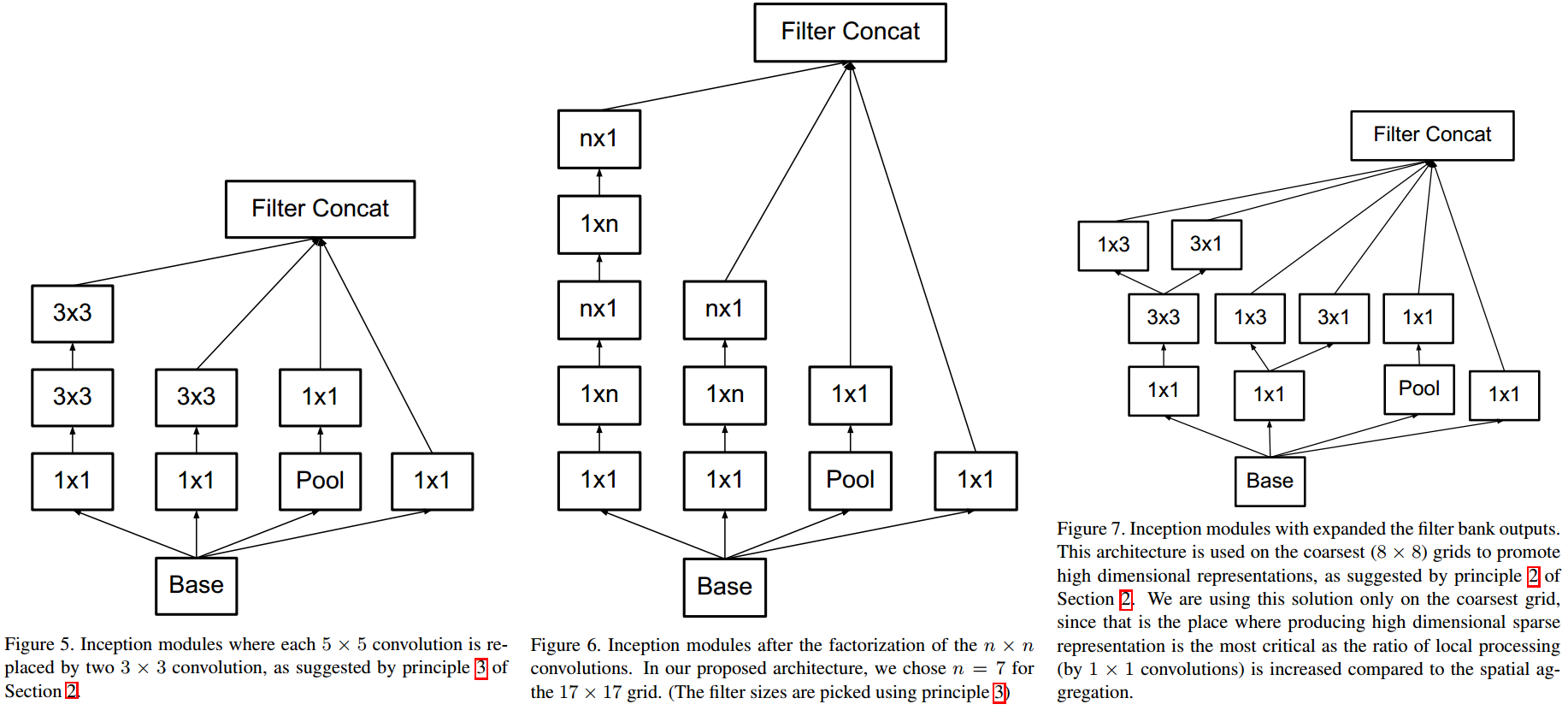
• Factorized Convolution（Inception V2），二维卷积变为行列分别卷积，先行卷积再列卷积，

  \[(K \times K) \rightarrow (K \times 1 + 1 \times K)
  \]

  

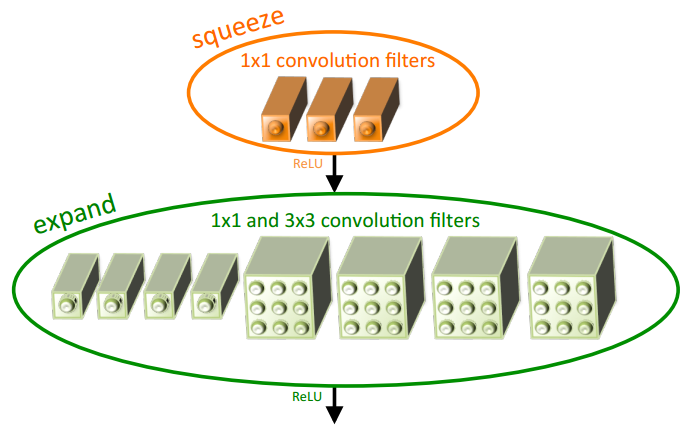
• Fire module（SqueezeNet），pointwise+ReLU+(pointwise + 3x3 conv)+ReLU，pointwise降维，同时将一定比例的\(3\times 3\)卷积替换为为\(1 \times 1\)，

  \[(K \times K \times M \times N) \rightarrow (M \times \frac{N}{t} + \frac{N}{t} \times (1-p)N + K \times K \times \frac{N}{t} \times pN) \\
  K = 3
  \]

  

• Bottleneck（ResNet），pointwise+BN ReLU+3x3 conv+BN ReLU+pointwise，类似于对channel维做SVD，

  \[(K \times K \times M \times N) \rightarrow (M \times \frac{N}{t} + K \times K \times \frac{N}{t} \times \frac{N}{t} + \frac{N}{t} \times N) \\
  t = 4
  \]

  

• ResNeXt Block（ResNeXt），相当于引入了group \(3\times 3\) convolution的bottleneck，

  

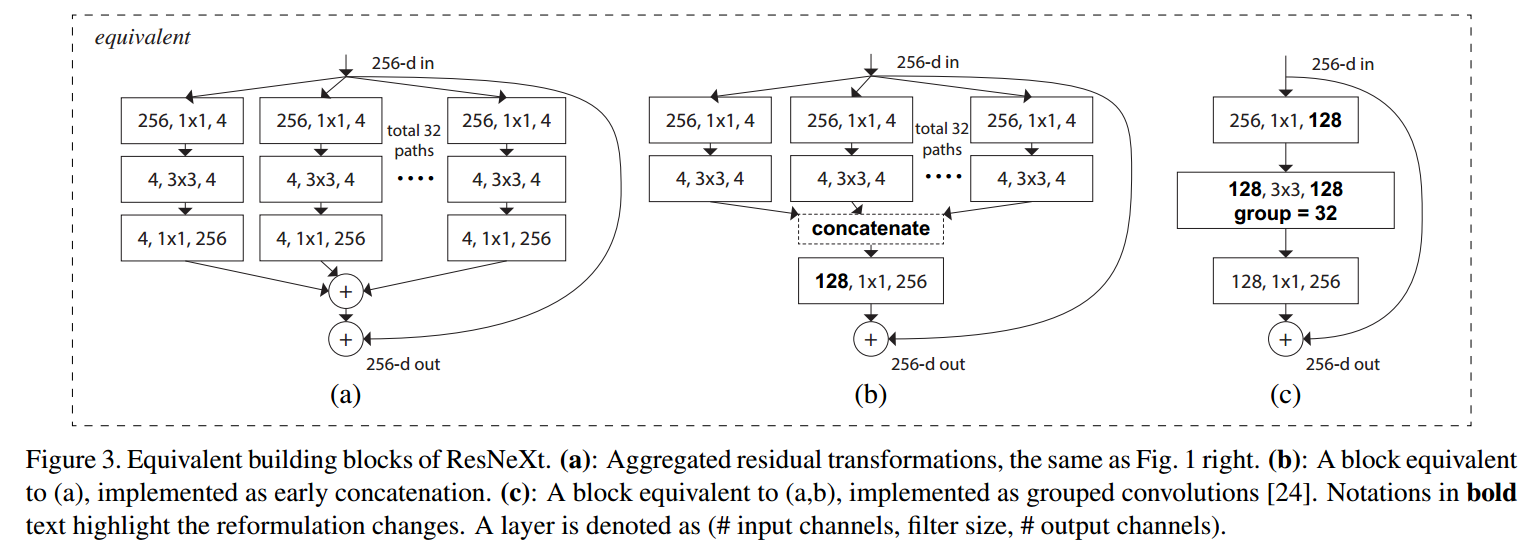  \[(K \times K \times M \times N) \rightarrow (M \times \frac{N}{t} + K \times K \times \frac{N}{tG} \times \frac{N}{t} + \frac{N}{t} \times N) \\
  t = 2, \ G = 32
  \]

• Depthwise Separable Convolution（MobileNet V1），depthwise +BN ReLU + pointwise + BN ReLU，

  

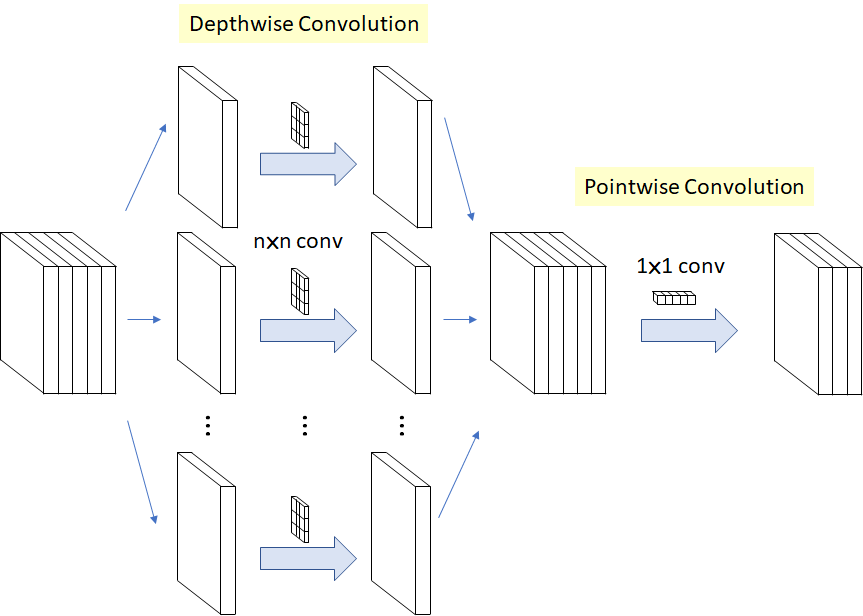
  相当于将channel维单独分解出去，

  \[(K \times K \times N) \rightarrow (K \times K + N)
  \]

• Separable Convolution（Xception），pointwise + depthwise + BN ReLU，

  

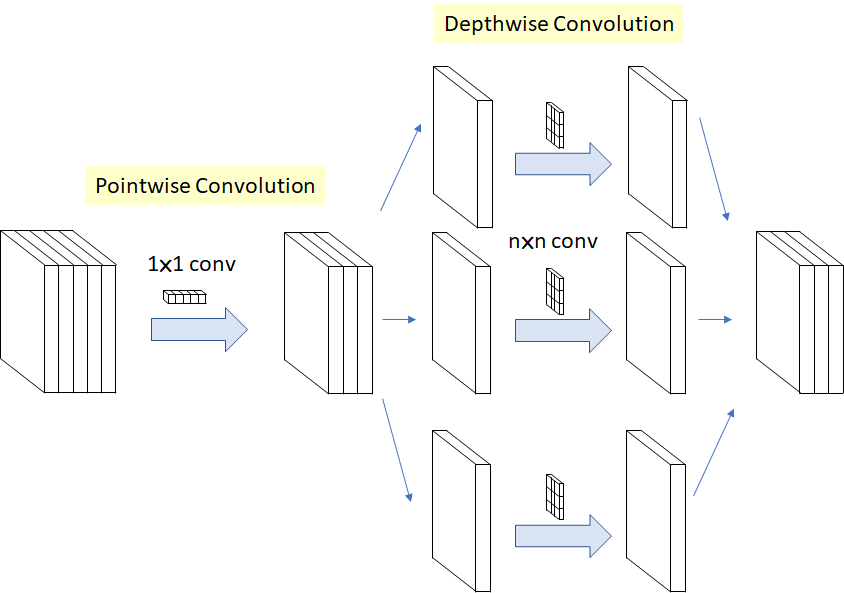
  也相当于将channel维分解出去，但前后顺序不同（但因为是连续堆叠，其实跟基本Depthwise Separable Convolution等价），同时移除了两者间的ReLU，

  \[(K \times K \times M) \rightarrow (M + K \times K)
  \]

  但实际在实现上是depthwise + pointwise + ReLU。

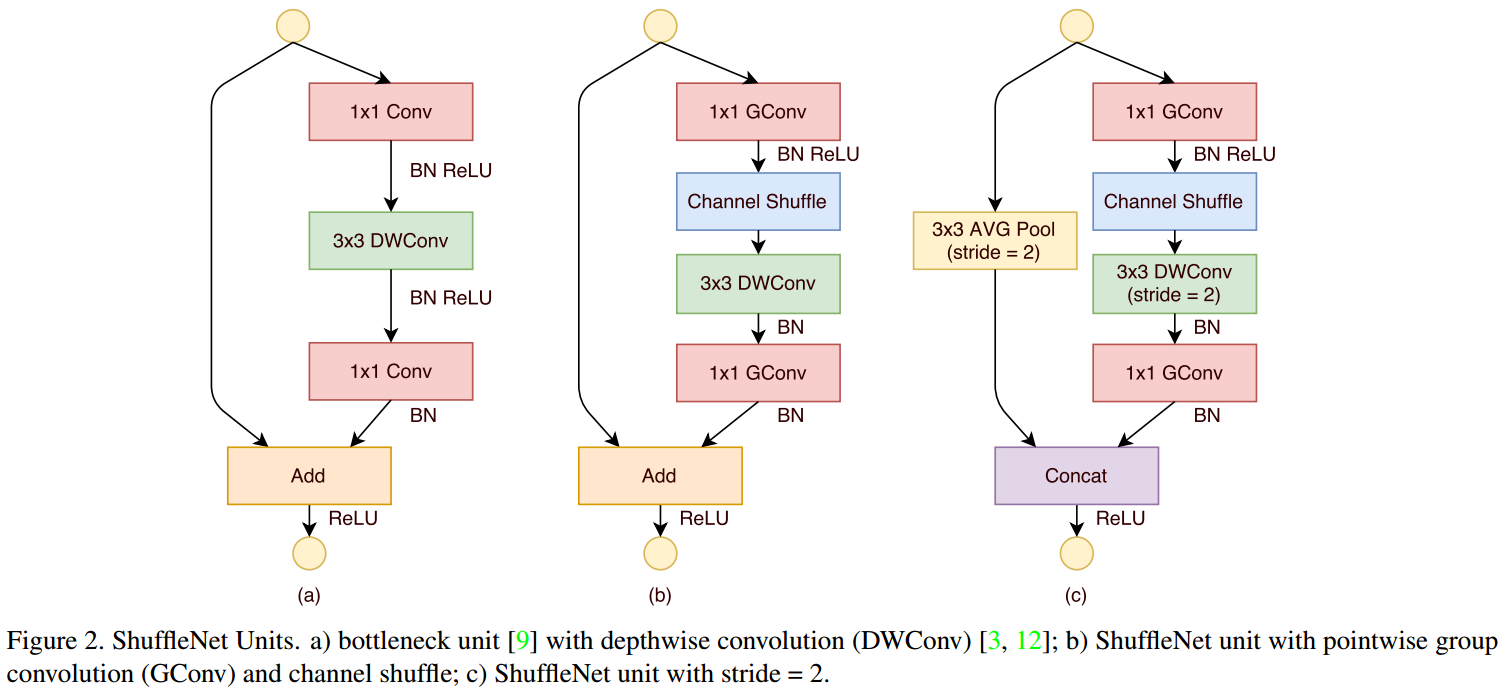
• pointwise group convolution and channel shuffle（ShuffleNet），group pointwise+BN ReLU+Channel Shuffle+depthwise+BN+group pointwise+BN，相当于bottleneck中2个pointwise引入相同的group，同时\(3\times 3\) conv变成depthwise，也就是说3个卷积层都group了，这会阻碍不同channel间（分组间）的信息交流，所以在第一个group pointwise后加入了channel shuffle，即

  \[(K \times K \times M \times N) \rightarrow (\frac{M}{G} \times \frac{N}{t} + channel \ shuffle +K \times K \times \frac{N}{t} + \frac{N}{tG} \times N)
  \]

  

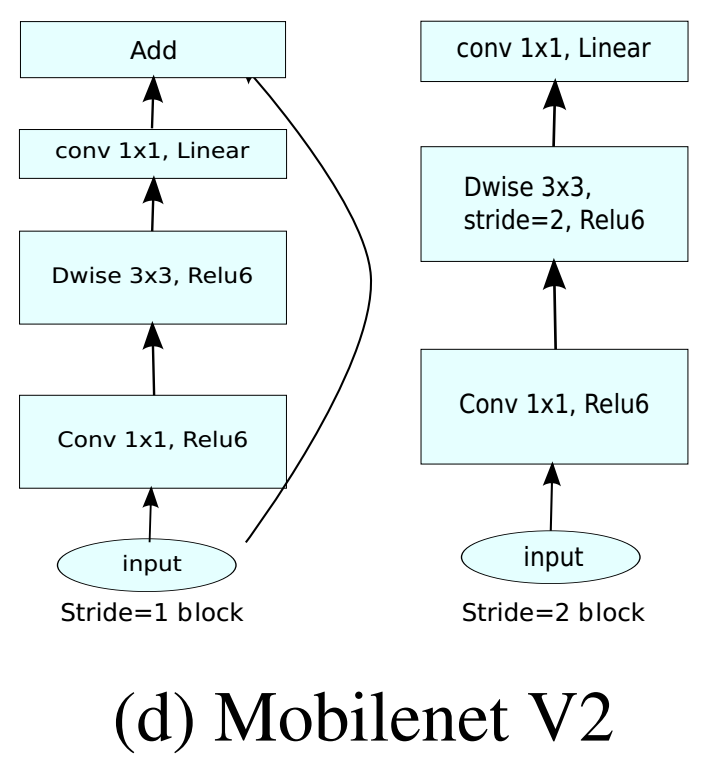
• Inverted Linear Bottleneck（MobileNet V2），bottleneck是先通过pointwise降维、再卷积、再升维，Inverted bottleneck是先升维、再卷积、再降维，pointwise+BN ReLU6+depthwise+BN ReLU6+pointwise+BN，

  \[(K \times K \times M \times N) \rightarrow (M \times tM + K \times K \times tM + tM \times N) \\t = 6
  \]

  

小结

最后小结一下，早期的CNN由一个个常规卷积层堆叠而成，而后，开始模块化，由一个个 module构成，module的演化，可以看成是不停地在常规卷积的计算量\(FLOPS = K \times K \times M \times N \times I \times I\)上做文章。

• 拆分：卷积核是个3 D 的tensor，可以在不同维度上进行拆分，行列可拆分，高上也可拆分，高上还可以多段拆分（类似SVD）。
• 分组：如果多个卷积核放在一起，可以构成4D的tensor，增加的这一数量维上可以分组group。

不同拆分和分组的方式排列组合就构成了各种各样的module。