从多种角度看[BZOJ 1061] [NOI 2008]志愿者招募(费用流)

题面

申奥成功后，布布经过不懈努力，终于成为奥组委下属公司人力资源部门的主管。布布刚上任就遇到了一个难题：为即将启动的奥运新项目招募一批短期志愿者。经过估算，这个项目需要N 天才能完成，其中第i 天至少需要Ai 个人。布布通过了解得知，一共有M 类志愿者可以招募。其中第i 类可以从第Si 天工作到第Ti 天，招募费用是每人Ci 元。新官上任三把火，为了出色地完成自己的工作，布布希望用尽量少的费用招募足够的志愿者，但这并不是他的特长！于是布布找到了你，希望你帮他设计一种最优的招募方案。

分析

感觉这个问题已经成为一个经典套路了。先把问题形式化:

给出一条直线上的$n$个点，$m$个区间$[l_i,r_i]$。选一些区间覆盖这条直线，使得每个点至少被覆盖$a_i$次，每个区间可以被用来覆盖多次,每覆盖一次的代价为$c_i$.求最小代价。

接下来我们将从多个角度建图:

从流量守恒的角度理解

这里先给出建图方式,记$(u,v,w,c)$表示从$u$到$v$连一条容量为$w$,费用为$c$的有向边:

建立源汇点$s,t$,连边$(s,1,+\infty,0),\ (n+1,t,+\infty,0)$
对于每个区间$[l_i,r_i]$,连边$(l_i,r_i+1,+\infty,c_i)$
对于每个点$i$,连边$(i,i+1,\infty-a_i)$

对于每个区间$[l_i,r_i]$,连边$(l_i,r_i+1,+\infty,c_i)$不难理解，+1是为了把覆盖点转化成覆盖边。比如$l_i=r_i$时区间$[l_i,r_i]$正好就覆盖了$a_{l_i}$所在的那条边。

如何理解$\infty-a_i$？我们考虑到覆盖点$i$的每个区间，每个区间的使用次数加起来$\geq a_i$.也就是说，跨过边$(i,i+1)$的那些边的流量之和至少为$a_i$.

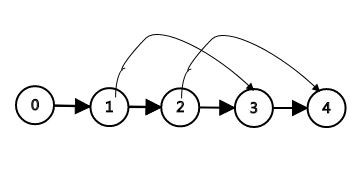
现在我们要保证上面的条件。注意到我们从源点流出的流量为$+\infty$,流入汇点的流量也是$+\infty$。对于一条边$(i,i+1,\infty-a_i,0)$，它最多只能流掉$\infty-a_i$的流量。而为了保证流量守恒，跨过它的边至少要流掉剩下$a_i$的流量，否则总流量就不是$\infty$了。这样的话，跨过$(i,i+1)$的边的流量之和就至少为$a_i$了。满足了上面的条件。

如果不好理解可以看图，假如a[2]=3,那么(2,3)上面的两条边就需要流掉3的流量，否则流量就不守恒了。

从线性规划的角度理解

对于一些不太好直接想到建图的问题，我们可以数学建模，列出方程然后用线性规划求解。这样的好处是思维量较小，只要做代数变换就可以建图，而不用考虑建图的实际意义。

对于每个区间，我们设它的覆盖次数为$x_i$,那么对于每个点$i$,我们有:

\[p_i=\sum_{l_j \leq i \leq r_j} x_j \geq a_i
\]

把不等式转化为等式,添加辅助变量$y_i(y_i \geq 0)$

\[p_i=\sum_{l_j \leq i \leq r_j} x_j -y_i = a_i
\]

用$p_i$减去$p_{i-1}$(特别地，我们规定$p_0=0,p_{n+1}=0$),得到:

$p_i-p_{i-1}=\sum_{l_j \leq i \leq r_j} x_j - \sum_{l_j \leq i-1 \leq r_j}x_j -y_i+y_{i-1}=a_i-a_{i-1}$

我们会发现，$x_j$的系数为正当且仅当区间$[l_j,r_j]$的左端点在$i$.因为这样第二个和式里一定没有$x_j$

$x_j$的系数为负当且仅当$[l_j,r_j]$的右端点在$i-1$,因为这样第一个和式里一定没有$x_j$

其他的$x_j$均被消掉

这样的话，每个变量都只在两个式子中出现了,而且一次为正，一次为负。所有等式右边和为0 .

我们举个例子来理解

例子来自byvoid巨佬的博客

一共需要4天，四天需要的人数依次是4,2,5,3。有5类志愿者，如下表所示：

种类 1 2 3 4 5

时间 [1,2] [1,1] [2,3] [3,3] [3,4]

费用 3 4 3 5 6

根据我们上面的描述，可以列出式子

\[\begin{cases} p_1= x_1 + x_2 - y_1 = 4 \\ p_2 = x_1 + x_3 - y_2 = 2\\ p_3 = x_3 + x_4 +x_5 - y_3 =5\\ p_4 = x_5 - y_4 = 3 \end{cases}
\]

然后做差

\[\begin{cases} p_1 -p_0 = x_1 + x_2 - y_1 = 4 \\ p_2 - p_1 = x_3 - x_2 -y_2 +y_1 = -2 \\ p_3 - p_2 = x_4 + x_5 - x_1 - y_3 + y_2 =3 \\p_4 - p_3 = - x_3 - x_4 + y_3 - y_4 = -2 \\p_5 - p_4 = - x_5 + y_4 = -3 \\ \end{cases}
\]

容易发现,每个变量都只在两个式子中出现了,而且一次系数为正，一次系数为负。所有等式右边的常数之和为0 .

种类	1	2	3	4	5
时间	[1,2]	[1,1]	[2,3]	[3,3]	[3,4]
费用	3	4	3	5	6

我们最终的目的是在上面方程组的约束条件下最优化目标函数 $\sum_{j=1}^m x_j c_j$。这里当然可以用单纯形算法解决，但是本人太弱不会，于是考虑建图跑网路流解决。

根据网络流中每个点流量平衡的思想，我们可以把$-x_i$看成从点$i$流出$x_i$的流量，$+x_i$看成流入$x_i$的流量。等式为0就代表流量平衡。

每个等式为图中一个顶点，添加源点S和汇点T。
如果一个等式右边为非负整数c，从源点S向该等式对应的顶点连接一条容量为c，权值为0的有向边；如果一个等式右边为负整数c，从该等式对应的顶点向汇点T连接一条容量为c，权值为0的有向边。
如果一个变量$x_i$在第j个等式中出现为$x_i$，在第k个等式中出现为$-x_i$，且在目标函数里的系数为$c_i$,从顶点j向顶点k连接一条容量为$+\infin$，费用为$c_i$的有向边。
如果一个变量$y_i$在第j个等式中出现为$y_i$，在第k个等式中出现为$-y_i$，且在目标函数里没有出现，从顶点j向顶点k连接一条容量为$+\infin$，权值为0的有向边。

具体到这个问题上，最终的建图方案是:

建立源点S=0,汇点T=n+2
若$a_i-a_{i-1}>0$ 连边$(S,i,a_i-a_{i-1},0)$,否则连边$(i,T,a_{i-1}-a_{i},0)$.($i \in[1,n+1],a_0=a_{n+1}=0$)
对于每个区间$[l_j,r_j]$,连边$(l_j,r_j+1,+\infin,c_i)$ (对应方程中的$x$)
对于$i \in [1,n]$ 连边$[i+1,i, +\infty,0]$ (对应方程中的$y$)

代码

第一种建图:

#include<iostream>

#include<cstdio>

#include<cstring>

#include<queue>

#define INF 0x3f3f3f3f

#define maxn 50000

#define maxm 500000

using namespace std;

inline void qread(int &x){

    x=0;

    int sign=1;

    char c=getchar();

    while(c<'0'||c>'9'){

        if(c=='-') sign=-1;

        c=getchar();

    }

    while(c>='0'&&c<='9'){

        x=x*10+c-'0';

        c=getchar();

    }

    x=x*sign;

}

int n,m;

struct edge {

    int from;

    int to;

    int next;

    int flow;

    int cost;

} E[maxm*2+5];

int sz=1;

int head[maxn+5];

int pre[maxn+5];

int minf[maxn+5];

int dist[maxn+5];

int inq[maxn+5];

void adde(int u,int v,int w,int c) {

    sz++;

    E[sz].from=u;

    E[sz].to=v;

    E[sz].flow=w;

    E[sz].cost=c;

    E[sz].next=head[u];

    head[u]=sz;

}

void add_edge(int u,int v,int w,int c){

//  printf("%d->%d vol=%d cost=%d\n",u,v,w,c);

    adde(u,v,w,c);

    adde(v,u,0,-c);

}

int spfa(int s,int t){

    queue<int>q;

    memset(dist,0x3f,sizeof(dist));

    memset(inq,0,sizeof(q));

    q.push(s);

    dist[s]=0;

    inq[s]=1;

    while(!q.empty()){

        int x=q.front();

        q.pop();

        inq[x]=0;

        for(int i=head[x];i;i=E[i].next){

            int y=E[i].to;

            if(E[i].flow){

//              printf("%d %d\n",x,y);

                if(dist[y]>dist[x]+E[i].cost){

                    dist[y]=dist[x]+E[i].cost;

                    minf[y]=min(minf[x],E[i].flow);

                    pre[y]=i;

                    if(!inq[y]){

                        inq[y]=1;

                        q.push(y);

                    }

                }

            }

        }

    }

    if(dist[t]==INF) return 0;

    else return 1;

}

void update(int s,int t){

    int x=t;

    while(x!=s){

        int i=pre[x];

        E[i].flow-=minf[t];

        E[i^1].flow+=minf[t];

        x=E[i^1].to;

    }

}

int mcmf(int s,int t){

    int maxcost=0,maxflow=0;

    memset(minf,0x3f,sizeof(minf));

    while(spfa(s,t)){

        update(s,t);

        maxcost+=minf[t]*dist[t];

        maxflow+=minf[t];

    }

    return maxcost;

}

int a[maxn+5];

int main(){

	int u,v,w;

	qread(n);

	qread(m);

	for(int i=1;i<=n;i++){

		qread(a[i]);

	}

	for(int i=1;i<=m;i++){

		qread(u);

		qread(v);

		qread(w);

		add_edge(u,v+1,INF,w);

	}

	int s=0,t=n+2;

	add_edge(0,1,INF,0);

	add_edge(n+1,t,INF,0);

	for(int i=1;i<=n;i++){

		add_edge(i,i+1,INF-a[i],0);

	}

	printf("%d\n",mcmf(s,t));

}

第二种建图:

#include<iostream>

#include<cstdio>

#include<cstring>

#include<queue>

#define INF 0x3f3f3f3f

#define maxn 50000

#define maxm 500000

using namespace std;

inline void qread(int &x){

    x=0;

    int sign=1;

    char c=getchar();

    while(c<'0'||c>'9'){

        if(c=='-') sign=-1;

        c=getchar();

    }

    while(c>='0'&&c<='9'){

        x=x*10+c-'0';

        c=getchar();

    }

    x=x*sign;

}

int n,m;

struct edge {

    int from;

    int to;

    int next;

    int flow;

    int cost;

} E[maxm*2+5];

int sz=1;

int head[maxn+5];

int pre[maxn+5];

int minf[maxn+5];

int dist[maxn+5];

int inq[maxn+5];

void adde(int u,int v,int w,int c) {

    sz++;

    E[sz].from=u;

    E[sz].to=v;

    E[sz].flow=w;

    E[sz].cost=c;

    E[sz].next=head[u];

    head[u]=sz;

}

void add_edge(int u,int v,int w,int c){

//	printf("%d->%d vol=%d cost=%d\n",u,v,w,c);

	adde(u,v,w,c);

	adde(v,u,0,-c);

}

int spfa(int s,int t){

    queue<int>q;

    memset(dist,0x3f,sizeof(dist));

    memset(inq,0,sizeof(q));

    q.push(s);

    dist[s]=0;

    inq[s]=1;

    while(!q.empty()){

        int x=q.front();

        q.pop();

        inq[x]=0;

        for(int i=head[x];i;i=E[i].next){

            int y=E[i].to;

            if(E[i].flow){

//            	printf("%d %d\n",x,y);

                if(dist[y]>dist[x]+E[i].cost){

                    dist[y]=dist[x]+E[i].cost;

                    minf[y]=min(minf[x],E[i].flow);

                    pre[y]=i;

                    if(!inq[y]){

                        inq[y]=1;

                        q.push(y);

                    }

                }

            }

        }

    }

    if(dist[t]==INF) return 0;

    else return 1;

}

void update(int s,int t){

    int x=t;

    while(x!=s){

        int i=pre[x];

        E[i].flow-=minf[t];

        E[i^1].flow+=minf[t];

        x=E[i^1].to;

    }

}

int mcmf(int s,int t){

	int maxcost=0,maxflow=0;

	memset(minf,0x3f,sizeof(minf));

	while(spfa(s,t)){

		update(s,t);

		maxcost+=minf[t]*dist[t];

		maxflow+=minf[t];

	}

	return maxcost;

}

int a[maxn+5];

int main(){

	int u,v,w;

	qread(n);

	qread(m);

	for(int i=1;i<=n;i++){

		qread(a[i]);

	}

	for(int i=1;i<=m;i++){

		qread(u);

		qread(v);

		qread(w);

		add_edge(u,v+1,INF,w);

	}

	int s=0,t=n+2;

	for(int i=1;i<=n+1;i++){

		int c=a[i]-a[i-1];

		if(c>=0){

			add_edge(s,i,c,0);

		}else{

			add_edge(i,t,-c,0);

		}

	}

	for(int i=1;i<=n;i++) add_edge(i+1,i,INF,0);

	printf("%d\n",mcmf(s,t));

}