数据结构之双端队列（Deque）

1，双端队列定义

　　双端队列：其两端都可以入列和出列的数据结构，如下图所示，队列后面（rear）可以加入和移出数据，队列前面（front）可以加入和移出数据

　　　　

　　双端队列操作：

deque=Deque()  # 创建双端队列
addFront(item)   #在队列前面加入数据
addRear(item)    #在队列后面加入数据
removeFront()    #在队列前面移除数据
removeRear()     #在队列后面移除数据
isEmpty()           #返回队列是否为空
size()                 #返回队列大小

　　操作示例：

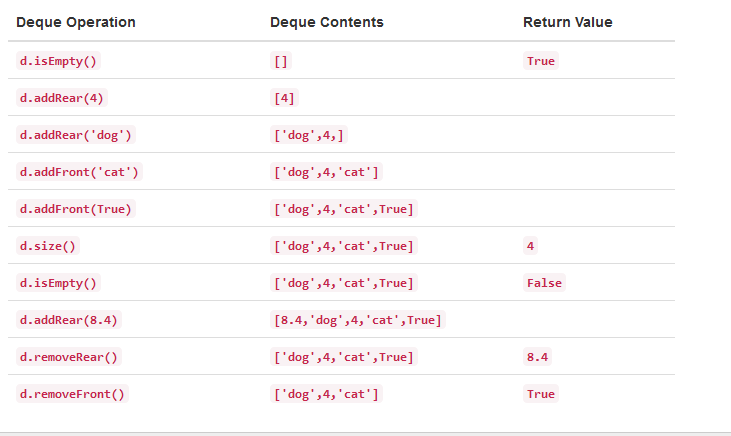
2， 用python实现双端队列

　　　Deque的代码实现如下：　

class Deque(object):
    def __init__(self):
        self.items=[]

    def addFront(self,item):
        self.items.append(item)  

    def addRear(self,item):
        self.items.insert(0, item)

    def removeFront(self):
        return self.items.pop()

    def removeRear(self):
        return self.items.pop(0)

    def size(self):
        return len(self.items)

    def isEmpty(self):
        return self.items==[]
    

3，Deque的应用

　　回文检查（Palindrome checker）：检查字符序列是否为回文（回文指正读和反读都相同的字符序列，如 madam, 123321）。实现代码如下：

#检测字符序列是否为回文
def palChecker(palString):
    dq = Deque()
    for i in palString:
        dq.addFront(i)

    while dq.size()>1:
        first = dq.removeFront()
        last = dq.removeRear()
        if first!=last:
            return False
    return True
print palChecker("lsdkjfskf")
print palChecker("radar")