SIGAI深度学习第六集 受限玻尔兹曼机

讲授玻尔兹曼分布、玻尔兹曼机的网络结构、实际应用、训练算法、深度玻尔兹曼机等。受限玻尔兹曼机（RBM）是一种概率型的神经网络。和其他神经网络的区别：神经网络的输出是确定的，而RBM的神经元的输出值是不确定的，以某种概率取到某一个值、以另一种概率取到另一个值，神经元的输出值。各个神经元的输入值服从某种概率分布，所有神经元的输出值服从玻尔兹曼分布。

大纲：

玻尔兹曼分布

网络结构

计算隐藏单元的值

用于特征提取

训练算法

深度玻尔兹曼机

本集总结

玻尔兹曼分布：

玻尔兹曼分布是统计物理中的一种概率分布，描述系统处于某种状态x的概率分布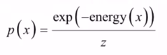：，z是归一化因子，即x分布的概率之和为1，x是离散型随机变量。

 网络结构：

可见单元-输入数据（已知）

隐藏单元-设计得到的结果

二部图-图的节点集合被划分成两个不相交的子集，这两个子集内的节点之间没有边连接，子集之间的节点之间有边连接，子集之间的节点之间有边连接。

可见单元和隐藏单元的值服从玻尔兹曼机分布（v是可见单元，h是隐藏单元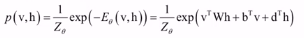）：，其中能量由状态（可见单元v和隐藏单元h的值）决定定义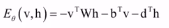：，归一化因子：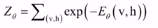

RBM特征自动提取任务：根据v的值得到模型的参数W、h确定之后，根据p(v,h)求出h的值和对应的概率分布（只取0或1的值），这些h的概率取值组成的向量[0,1,0,0,1,...]就是提取出来的特征向量。

受限玻尔兹曼机的三个要点：

1.随机性的神经网络，每个神经元以某种概率分布取值，只取0或1，如取1概率0.3，或0概率0.7。

2.由可见单元和隐藏单元组成二部图，即连接受限。

3.所有神经元v、h的值（0或1）的取值概率服从玻尔兹曼分布。

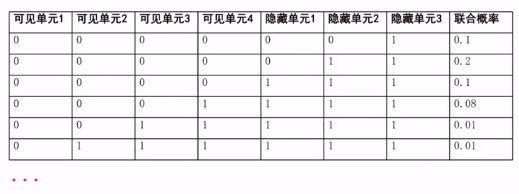
实际例子：即v和h的离散型概率分布，每一行表示已知输入向量和一个特征向量和特征向量取该值时的概率。

计算隐藏单元的条件：

v一般是输入数据X，h是从X提出的一个特征向量Y，即给定一个输入X提出的特征向量不是确定的有很多可能，即Y服从某个概率分布，因此要求（v,h）概率分布。

计算隐藏单元的值：实际使用时，给定可见变量的值，根据模型参数可以得到隐藏变量的条件概率密度函数，根据条件概率的计算公式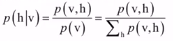：，将p(v,h)的定义带入上式得：

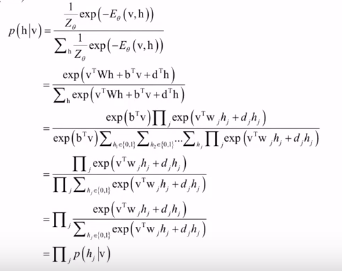
一旦知道了p(v|h)，就可以生成特征向量h了。

计算单个隐藏单元的条件概率：

隐含节点之间没有连接，因此这些随机变量是相互独立的，即p(h|v)=p(h₁|v)...p(h_n|v)。

已知可见变量时某一个隐含变量的值为1的概率：

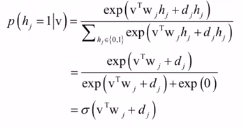
会发现该概率服从逻辑斯蒂回归预测函数，二分类问题。

用于特征提取：

可见单元作为输入数据，隐藏单元作为特征向量

计算隐藏层神经元的激励能量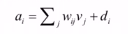

计算该隐藏单元的条件概率值，即状态为1的概率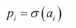

以p_i的概率将隐藏层神经元的状态值设置为1，以1-p_i的概率将其设置为0。

训练算法：

P(v,h)~(W,b,d)，一般概率分布参数值用最大似然估计，但是这里h不知道，因此不可以用，这里用Contrastive Divergence算法，此算法用的不多不必深究。

 深度玻尔兹曼机：

同深层自动编码器类似，可以将多个受限玻尔兹曼机层叠加起来使用，通过多层的受限玻尔兹曼机，可以完成数据在不同层次上的特征提取和抽象。

v——>h——>v——>h——>...，一个层的h层作为一次层v的输入值，训练时，也是从前往后逐层训练。

本集总结：

自动编码器、受限玻尔兹曼机，在实际应用中用的很少了，主要是深度学习发展早期的理论性的方法，只需记住他们的精髓就行了。