二叉查找树 & B(B-)树 & B+树 & B*树

一 二叉查找树

1 特点

（1）所有非叶子结点至多拥有两个子节点, left和right

（2）一个结点存储一个关键字

（3）非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树

2 数据结构

3 说明

二叉搜索树查找元素的过程:

从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；

否则，如果查询关键字比结点关键字小，就进入左儿子；

如果比结点关键字大，就进入右儿子；

如果左儿子或右儿子的指针为空，则找不到相应的关键字；

二叉查找树最好的搜索性能逼近二分(非叶子节点子树节点平衡)，最坏的性能是线性的，参看下图

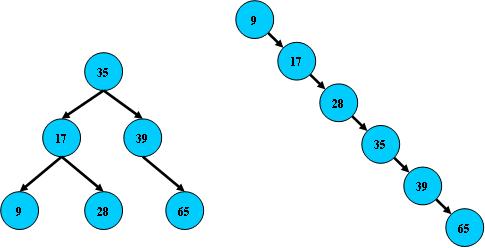
在基本平衡的情况下，二叉树比连续内存空间的二分查找的优点是，改变B树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；

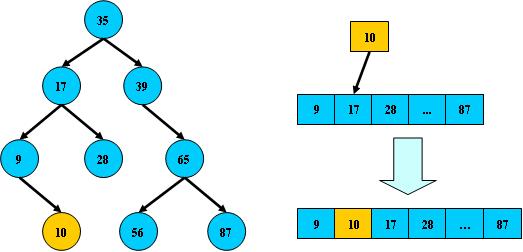
AVL

二 B(B-树)

⚠️B树和B-树是同一种树，只不过英语中B-tree被中国人翻译成了B-树，让人以为B树和B-树是两种树，实际上，两者就是同一种树

1 特点

是一种多路搜索树（并不一定是二叉的）

（1）定义任意非叶子结点最多只有M个儿子；且M>2；

（2）根结点的儿子数为[2, M]；

（3）除根结点以外的非叶子结点的儿子数为[M/2, M]；

（4）每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

（5）非叶子结点的关键字个数=指向儿子的指针个数-1；

（6）非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

（7）非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

（8）所有叶子结点位于同一层；

2 数据结构（M=3）

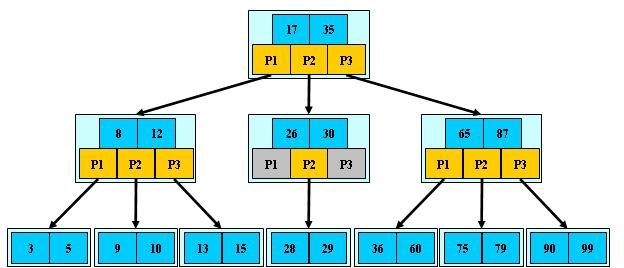
3 说明

B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点；

B-树的特性：

1.关键字集合分布在整颗树中；

2.任何一个关键字出现且只出现在一个结点中；

3.搜索有可能在非叶子结点结束；

4.其搜索性能等价于在关键字全集内做一次二分查找；

5.自动层次控制；

由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少利用率，其最底搜索性能为：

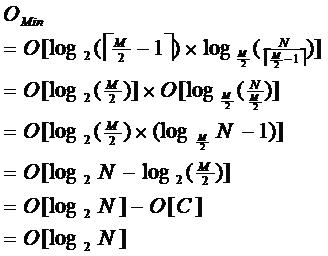
其中，M为设定的非叶子结点最多子树个数，N为关键字总数；

所以B-树的性能总是等价于二分查找（与M值无关），也就没有二叉树平衡的问题；

由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

三 B+树

1 特点

B+树是B-树的变体，也是一种多路搜索树：

（1）其定义基本与B-树同，除了：

（2）非叶子结点的子树指针与关键字个数相同；

（3）非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树（B-树是开区间）；

（4）为所有叶子结点增加一个链指针；

（5）所有关键字都在叶子结点出现；

2 数据结构（M=3）

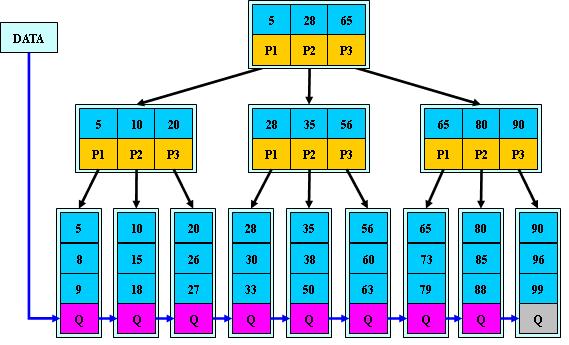
3 说明

B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+的特性：

1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；

2.不可能在非叶子结点命中；

3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；

4.更适合文件索引系统；

5.在B+Tree的每个叶子节点增加一个指向相邻叶子节点的指针，就形成了带有顺序访问指针的B+Tree。做这个优化的目的是为了提高区间访问的性能，例如图中如果要查询key为从20到33的所有数据记录，当找到20后，只需顺着节点和指针顺序遍历就可以一次性访问到所有数据节点，极大提到了区间查询效率。

四 B*树

1 特点

是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针

2 数据结构

3 说明

B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）；

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

五 小结

B树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；

所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

六 扩展

1 AVL树

AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。

2 红黑树简介

R-B Tree(Red-Black Tree), 称为红黑树，它是一种特殊的二叉查找树，每个节点都有存储位表示节点的颜色，可以是红或者黑

红黑树的特性:
（1）每个节点或者是黑色，或者是红色。
（2）根节点是黑色。
（3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点，是指为空(NIL或NULL)的叶子节点！]
（4）如果一个节点是红色的，则它的子节点必须是黑色的。
（5）从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

注意：
(01) 特性(3)中的叶子节点，是只为空(NIL或null)的节点。
(02) 特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

 红黑树的应用:

红黑树的应用比较广泛，主要是用它来存储有序的数据，它的时间复杂度是O(log n)，效率非常之高。
例如，Java集合中的TreeSet和TreeMap，C++ STL中的set、map，以及Linux虚拟内存的管理，都是通过红黑树去实现的。

3 AVL树和红黑树区别

AVL是严格的平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多；

红黑树是用非严格的平衡来换取增删节点时候旋转次数的开销；

所以简单说，如果你的应用中，搜索的次数远远大于插入和删除，那么选择AVL树，

如果搜索，插入删除次数几乎差不多，应选择红黑树。即，有时仅为了排序（建立-遍历-删除），不查找或查找次数很少，R-B树合算一些。

红黑树与AVL树的调整平衡的实现机制不同，AVL靠平衡因子和旋转，红黑树靠节点颜色以及一些约定再加上旋转。因此，存在去掉颜色的红黑树后它不是AVL树，比如左子树都是黑的，右子树都是红黑相间的，这样整个树高度2n的时候，根节点的左右层数差可以到n。