ML_Review_SVM(Ch9)

Note sth about SVM(Support Vector Machine)

支持向量机（SVM）从入门到放弃再到掌握这篇博客讲得挺仔细。
动机：
  SVM的中文名字——支持向量机。本质是一种线性的二分类器。如果涉及多分类问题，一般有两种方法（假设一共有k类）：1、训练k个svm，每次训练时，把某个类设为+，而其余为-。2、训练$C{k \choose 2}$，即两两之间都训练一个svm。以上两种方法各有优劣，具体可移步SVM多分类的两种方式。

SVM算法：
考虑下图（图是偷拿老师ppt的）。

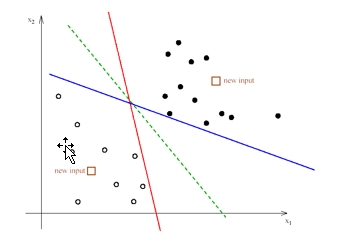
  如果我们需要选择一条直线，将上述样本（TrainingData）分为两类，哪条直线是我们希望使用的？（显然，三条线都可以很好的完成样本（TrainingData）的分类）。
  但是，直观感觉告诉我们，绿色的会较优。因为什么？因为绿色的线对局部的扰动性容忍度更高，更抗扰动。而这直观感受就是，两类点都离这条线较远，或者说两类点中离这条线最近的点，到这条线的距离较远。而这些最近的点，到线的映射点，两点的连线就是所谓的支持向量，和我们找到的直线平行的分别过两类点中离该直线最近的点的两条直线之间的距离就是间隔，我们需要间隔最大。不妨假设这两条直线为：
  a（$w^Tx+b \leq -1$）
  c（$w^Tx+b \geq 1$）
  而中间的直线为b（$w^Tx+b=0$）。
  称a，b（或者b，c）之间的距离为间隔（margin）。

算法公式概述：
  首先，我们定义样本为两类，+1，-1（+100，-100；+20，-5000……其实都可以，只不过+1，-1写出来式子比较好看）那么我们的分类标准就是，若$w^Tx+b \geq 1$则该样本（TestData）为正类，若$w^Tx+b \leq -1$则该样本（TestData）为负类。
  其次，不难得出：
$$margin= \frac{1}{2} ( \frac{w}{||w||}x_{+} + \frac{b}{||w||} - \frac{w}{||w||}x_{-} - \frac{b}{||w||} ) $$
$$ \rightarrow \frac{1}{2||w||}(wx_{+} + b - wx_{-} - b) = \frac{1}{||w||} $$
  为什么？因为$x_{+}$是$w^Tx+b = 1$上的点，$x_{-}$是$w^Tx+b = -1$上的点，所以上式$ wx_{+}+b-wx_{-}-b = (wx_{+}+b) - (wx_{-}-b) = 1 - (-1) = 2 $就约去了$\frac{1}{2||w||}$的分母中的2。我们希望我们最大化$\frac{1}{||w||}$，并且我们找到的这条直线$ w^Tx+b=0$的直线满足：
$$ wx_i + b \geq +1, \quad y_i = +1 $$
$$ wx_i + b \leq -1, \quad y_i = -1 $$
  即可以表示为：$y_{i}(wx_{i}+b)-1 \geq 0$
  于是乎，我们需要做的就是下面的式子：
$$ max \qquad \frac{1}{||w||} \qquad (1) $$
$$ s.t. \qquad y_i((wx_i)+b) \geq 1, \quad i = 1,2,...,n \qquad (2) $$
  而在实作的时候我们通常做的是(1)的式子的对偶形式，即：$max \quad \frac{1}{2}||w||^2 $
  最后观察式子，发现为有约束的优化问题，可引入拉格朗日乘子法解决，在此并不赘述。