luogu P4843 清理雪道

嘟嘟嘟




这其实就是一个最小流的板子题。把每一条边的流量至少为1，然后建立附加源汇跑一遍最大流，连上\(t, s\)，再跑一遍最大流就是答案。




刚开始我想错了：统计每一个点的出度和入度，去两者较大值\(w\)，则流经这个点的流量至少为\(w\)。所以我就拆点，从\(i\)向\(i'\)连一条容量为\([w, INF]\)的边，其他边没有容量限制。

但其实这种建图方式是错的，因为可以有一条边流了很多，满足了他出去的点的流量限制，从而导致有一些边没有走，使答案变小。

举个例子，

比如原图是这样的：



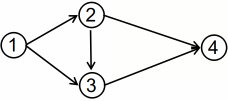
答案应该是3.

按我的想法，建出来的图是这样的：



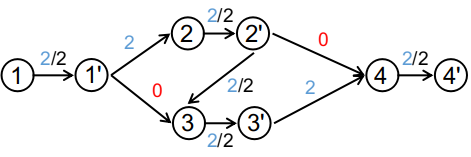
每一条边都符合了流量下限，但是却有两条边没流到，得到的结果是2。

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define In inline
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 105;
const int maxe = 1e6 + 5;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}

int n, s, t, S, T;
int du[maxn];
struct Edge
{
  int nxt, to, cap, flow;
}e[maxe];
int head[maxn << 1], ecnt = -1;
In void addEdge(int x, int y, int w)
{
  e[++ecnt] = (Edge){head[x], y, w, 0};
  head[x] = ecnt;
  e[++ecnt] = (Edge){head[y], x, 0, 0};
  head[y] = ecnt;
}

int dis[maxn << 1];
In bool bfs(int s, int t)
{
  Mem(dis, 0); dis[s] = 1;
  queue<int> q; q.push(s);
  while(!q.empty())
    {
      int now = q.front(); q.pop();
      for(int i = head[now], v; ~i; i = e[i].nxt)
	{
	  if(!dis[v = e[i].to] && e[i].cap > e[i].flow)
	    dis[v] = dis[now] + 1, q.push(v);
	}
    }
  return dis[t];
}
int cur[maxn << 1];
In int dfs(int now, int res, int t)
{
  if(now == t || res == 0) return res;
  int flow = 0, f;
  for(int& i = cur[now], v; ~i; i = e[i].nxt)
    {
      if(dis[v = e[i].to] == dis[now] + 1 && (f = dfs(v, min(res, e[i].cap - e[i].flow), t)) > 0)
	{
	  e[i].flow += f; e[i ^ 1].flow -= f;
	  flow += f; res -= f;
	  if(res == 0) break;
	}
    }
  return flow;
}

In int maxflow(int s, int t)
{
  int flow = 0;
  while(bfs(s, t))
    {
      memcpy(cur, head, sizeof(head));
      flow += dfs(s, INF, t);
    }
  return flow;
}

int main()
{
  Mem(head, -1);
  n = read(); s = 0, t = n + n + 1;
  S = t + 1, T = t + 2;
  for(int i = 1; i <= n; ++i)
    {
      addEdge(s, i, INF), addEdge(i, t, INF);
      int k = read(); du[i] += k;
      for(int j = 1; j <= k; ++j)
	{
	  int v = read(); --du[v];
	  addEdge(i, v, INF - 1);
	}
    }
  for(int i = 1; i <= n; ++i)
    if(du[i] >= 0) addEdge(i, T, du[i]);
    else addEdge(S, i, -du[i]);
  maxflow(S, T);
  addEdge(t, s, INF);
  write(maxflow(S, T)), enter;
  return 0;
}