题解 noip2019模拟赛Day1T3

题面

运河计划

问题描述

水运在人类的交通运输史中一直扮演着重要的角色.借助河流.的便利,人们得以把大量的货物输送到天南海北不仅仅是自然界现成的河流,人工开凿的运河(如苏伊士运河、巴拿马运河、我国的京杭大运河)都为文明的发展做出了卓越的贡献.

C 国计划建设若干条运河以沟通南北两大水系.鉴于奇奇怪怪的原因,建设只能沿棋盘式的网格交点及其连线进行,相关信息如下图所示:

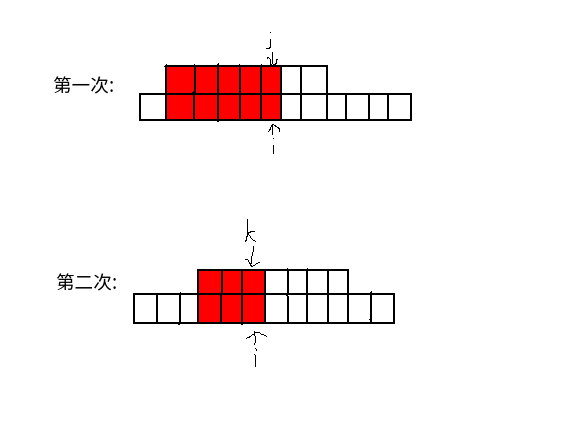
目标将河流 A 标红的港口与河流 B 标蓝的港口相连(红、蓝港口位置给定,数目相等,且都等于需要开凿的运河条数)为了节约维护成本,C 国的每条运河都是一条路径,并保证两两运河不同时经过任意交点.由于左上方的地势总比右下方高,为充分利用重力势能,可以开凿的线路为\((i,j)->(i+1,j)\),\((i,j)->(i,j+1)\)(保证坐标在(0, 0)到(n, m)范围内);同时,存在部分交点因为地形的缘故无法沟通其周围的河道(如图中的紫色五角星位置).

现在你的任务是计算有多少种合法的开凿方案(两种方案被看做不同,当它们存在任意一条线路开凿与否的情况同).

输入格式

第一行四个整数n、m、p、q,其中 p 为需要建设的运河条数,q 为不可开凿的交点个数; 第二行 p 个整数,分别表示河流 A 港口们的第二维坐标(第一维坐标均为 0);

第三行 p 个整数,分别表示河流 B 港口们的第二维坐标(第一维坐标均为 n);

以下 q 行每行两个整数 xi、yi,表示交点(xi, yi)不能被打通.

输出格式

一行一个整数表示方案数,对 998244353 取模.

输入样例1

4 4 2 1

0 2

1 4

2 3

输出样例1

30

输入样例2

10 10 4 1

0 2 3 5

1 4 6 8

2 3

输出样例2

4567992

数据范围

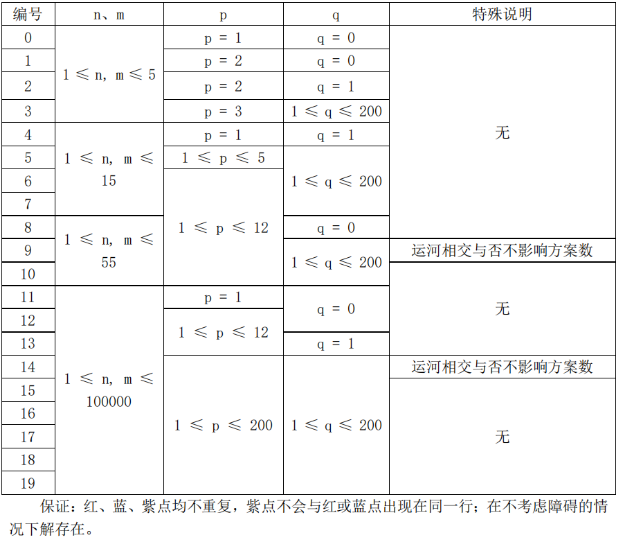
解析

首先我们考虑两个点\(A(x_1,y_1),B(x_2,y_2)\)之间的路径方案数,

显然是\(C_{x_2-x_1+y_2-y_1}^{y_2-y_1}\)(事实是考试的时候推了半天),

我们把它记作\(g(A,B)\)懒得写,

接下来我们来看中间有障碍物的情况.

很容易就能想到是容斥吧.

然而怎么容斥呢?

直接容斥肯定会炸掉.

但其实有一个巧妙的思路.

首先这个图可以看成一个DAG(因为只会往右,下流),

那么每个点就会有一个拓扑序,

其实就是按\(x,y\)排下序.

我们考虑每条道路首先经过的是哪个点,

这样就没有重复了.

具体来说,

我们设\(f[i]\)表示从起点\(S\)到\(i\)号障碍点,

经过的第一个障碍点是\(i\)的方案数.

那么显然\(f[1]=g(S,1)\).

而对于其他的\(i\),

\(f[i]\)就应该是\(g(S,i)\)再减掉首先经过拓扑序在它前面的每个点\(j\)再到\(i\)的方案数.

准确来说就是\(f[i]=g(S,i)-\sum\limits_jf[j]*g(j,i),x_j<=x_i,y_j<=y_i\)

然而讲了这么多到底有什么用?

毕竟我们还要考虑路径不相交的问题.

我们考虑两条路径\(a_i->b_i,a_j->b_j\),

如果它们有相交的话,我们可以假设它们在最后一个相交的点交换了路径,

于是路径就变成了\(a_i->b_j,a_j->b_i\),

于是我们对于上下的每个港口,

求出它们两两之间的路径方案数.

最后再容斥一下,

把没有交换的加起来,再减掉交换了两次的方案数......

然而到这里就完了?

我考场写到了这里但还是挂了.

因为你暴力统计有哪些交换了的肯定会炸掉啊!

其实到这里,我们只要仔细想想为什么我没想.

这正是行列式啊.(不懂行列式的请自行了解,不会懒得教)

我们只需要像高斯消元一样,

消成一个上三角矩阵,

最后把对角线乘起来就行了.

code:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define int ll
#define fre(x) freopen(x".in","r",stdin),freopen(x".out","w",stdout)
using namespace std;

inline int read(){
	int sum=0,f=1;char ch=getchar();
	while(ch>'9' || ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0' && ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
	return f*sum;
}

const int N=200001;
const int M=205;
const int Mod=998244353;
struct node{int x,y;}c[M];
int n,m,p,q,ans=1;
int a[M],b[M],f[M][M],d[M];
int jc[N],Inv[N];
int pla[M],v[M];

inline int fpow(int a,int b){
	int ret=1;
	while(b){
		if(b&1) ret=(ll)ret*a%Mod;
		a=(ll)a*a%Mod;b>>=1;
	}
	return ret;
}

inline int inv(int x){
	return fpow(x,Mod-2);
}

inline int C(int nn,int mm){
	if(mm>nn) return 0;
	return jc[nn]*Inv[nn-mm]%Mod*Inv[mm]%Mod;
}

inline bool cmp(node a,node b){return a.y!=b.y? a.y<b.y:a.x<b.x;}

inline int dis(int x1,int y1,int x2,int y2){
	return C(x2-x1+y2-y1,y2-y1);
}

signed main(){
	n=read();m=read();p=read();q=read();
	jc[0]=1;for(int i=1;i<N;i++) jc[i]=jc[i-1]*i%Mod;
	Inv[0]=1;for(int i=1;i<N;i++) Inv[i]=inv(jc[i]);
	for(int i=1;i<=p;i++) a[i]=read();
	for(int i=1;i<=p;i++) b[i]=read();
	for(int i=1;i<=q;i++) c[i].x=read(),c[i].y=read();
	sort(a+1,a+p+1);sort(b+1,b+p+1);
	sort(c+1,c+q+1,cmp);
	for(int i=1;i<=p;i++){
		for(int j=1;j<=q;j++) d[j]=0;
//		memset(d,0,sizeof(d));
		for(int j=1;j<=q;j++){
			if(c[j].y<a[i]) continue;
			d[j]=dis(0,a[i],c[j].x,c[j].y);
			for(int k=1;k<j;k++) d[j]=(d[j]-(d[k]*dis(c[k].x,c[k].y,c[j].x,c[j].y))+Mod)%Mod;
		}
		for(int j=1;j<=p;j++){
			if(b[j]<a[i]) continue;
			f[i][j]=dis(0,a[i],n,b[j]);
			for(int k=1;k<=q;k++){
				if(c[k].y<a[i]) continue;
				if(c[k].y>b[j]) break;
				f[i][j]=(f[i][j]-(d[k]*dis(c[k].x,c[k].y,n,b[j]))%Mod)%Mod;
			}
		}
	}
	int flag=1;
	for(int i=1;i<=p;i++){
		if(f[i][i]==0){
			for(int j=i+1;j<=p;j++){
				if(abs(f[j][i])>0){
					for(int k=1;k<=p;k++) swap(f[i][k],f[j][k]);
				flag*=-1;break;
				}
			}
		}
		for(int j=1;j<=p;j++){
			if(i==j) continue;
			int tem=f[j][i]*inv(f[i][i])%Mod;
			for(int k=1;k<=p;k++) f[j][k]=(f[j][k]-(f[i][k]*tem)+Mod)%Mod;
		}
	}
	for(int i=1;i<=p;i++) ans=ans*f[i][i]%Mod;
	printf("%lld\n",(ans*flag%Mod+Mod)%Mod);
	return 0;
}