矩阵快速幂(Matrix_Fast_Power)

一、基础知识
(1)矩阵乘法

https://blog.csdn.net/weixin_43272781/article/details/82899737

简单的说矩阵就是二维数组，数存在里面，矩阵乘法的规则:A*B=C

其中c[i][j]为A的第i行与B的第j列对应乘积的和，即: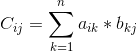

代码:

const int N=;
int c[N][N];
void multi(int a[][N],int b[][N],int n)//n是矩阵大小，n<N
{
    memset(c,,sizeof c);
    for(int i=;i<=n;i++)
        for(int j=;j<=n;j++)
        for(int k=;k<=n;k++)
        c[i][j]+=a[i][k]*b[k][j];
}

另一种写法:

int c[N][N];
void multi(int a[][N],int b[][N],int n)
{
    memset(c,,sizeof c);
    for(int i=;i<=n;i++)
        for(int k=;k<=n;k++)
        for(int j=;j<=n;j++)
        c[i][j]+=a[i][k]*b[k][j];
}

这种可以在第二重for判断if(a[i][k]==0)continue;对于矩阵有较多0的有一定效果。不过一般第一种写法就够了，这种知道就行。
显然矩阵乘法的复杂度是O(n^3);（O(n^2.7)的方法不会写，无视这里）。

这里我直接写的是n*n的矩阵(即方阵)，显然两个相乘是要一行和一列对应乘，那么矩阵乘法是需要A的行数与B的列数相等的(这是A*B的前提条件，可见矩阵的乘法是不满足交换律的)。然而这些一般都是没什么用的，矩阵快速幂只会用到方阵(除非题目是裸的矩阵乘法)。矩阵快速幂都是方阵也就避免的相乘的前提条件，可以放心用。

二、矩阵快速幂
如果不知道快速幂的请参考：https://www.cnblogs.com/DWVictor/p/10278589.html

const int N=;
int tmp[N][N];
void multi(int a[][N],int b[][N],int n)
{
memset(tmp,,sizeof tmp);
for(int i=;i<n;i++)
for(int j=;j<n;j++)
for(int k=;k<n;k++)
tmp[i][j]+=a[i][k]*b[k][j];
for(int i=;i<n;i++)
for(int j=;j<n;j++)
a[i][j]=tmp[i][j];
}
int res[N][N];
void Pow(int a[][N],int n)
{
memset(res,,sizeof res);//n是幂，N是矩阵大小
for(int i=;i<N;i++) res[i][i]=;
while(n)
{
if(n&)
multi(res,a,N);//res=res*a;复制直接在multi里面实现了；
multi(a,a,N);//a=a*a
n>>=;
}
}

值得注意的是矩阵快速幂只适用于n*n的矩阵方阵。

三、例题
http://poj.org/problem?id=3070

http://poj.org/problem?id=3233

http://acm.hdu.edu.cn/showproblem.php?pid=2276

http://acm.hdu.edu.cn/showproblem.php?pid=5015

https://ac.nowcoder.com/acm/contest/338/L

（题解：https://paste.ubuntu.com/p/8pMmJc6SDn/）