Haar-like特征来龙去脉

声明：引用请注明出处http://blog.csdn.net/lg1259156776/

haar-like特征概念

haar-like特征是是计算机视觉领域一种常用的特征描述算子。它最早是由Papageorigiou等人用于人脸描述。目前常用的Haar-like特征可以分为三类：线性特征、边缘特征、点特征（中心特征）、对角线特征。如下图所示

Haar特征（Haar-like features）是用于物体识别的一种数字图像特征。它们因为与Haar小波转换极为相似而得名，是第一种实时的人脸检测算子。

haar-like特征的特点

Haar特征值反映了图像的灰度变化情况。例如：脸部的一些特征能由矩形特征简单的描述，如：眼睛要比脸颊颜色要深，鼻梁两侧比鼻梁颜色要深，嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构，如边缘、线段较敏感，所以只能描述特定走向（水平、垂直、对角）的结构。

通过改变特征模板的大小和位置，可在图像子窗口中穷举出大量的特征。上图的特征模板称为“特征原型”；特征原型在图像子窗口中扩展（平移伸缩）得到的特征称为“矩形特征”；矩形特征的值称为“特征值”。

矩形特征可位于图像任意位置，大小也可以任意改变，所以矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化，使得很小的检测窗口含有非常多的矩形特征，如：在24*24像素大小的检测窗口内矩形特征数量可以达到16万个。这样就有两个问题需要解决了：（1）如何快速计算那么多的特征？—积分图；（2）哪些矩形特征才是对分类器分类最有效的？如通过AdaBoost算法来训练。

通过积分图快速计算haar-like特征

这方面的内容比较简单熟悉，不做过多总结。从下图和公式中可以看出：

设D的四个顶点分别为α、β、γ、δ，则D的像素和可以表示为

∑D=ii(α)+ii(β)−(ii(γ)+ii(δ))

而Haar-like特征值无非就是两个矩阵像素和的差，同样可以在常数时间内完成。

AdaBoost算法训练人脸分类器

最初的弱分类器可能只是一个最基本的Haar-like特征，计算输入图像的Haar-like特征值，和最初的弱分类器的特征值比较，以此来判断输入图像是不是人脸。这样一个弱分类实际上就是一个decision stump，决策树桩，就是说大于输入特征大于阈值就认为是人脸，小于则认为不是。

AdaBoost算法只需要求每个decision stump有略微比随机猜测要好的概率就行，也就是说略微大于50%。只要保证每个decision stump能够分别照顾不同的方面，也就是说decision stump之间具有差异性。举一个经典的例子如下：

老师问学生什么是苹果，每个同学说一个其它同学没说过的苹果的特点，比如同学A说苹果是圆的（形状特征），同学B说苹果是甜的（口味特征），同学C说苹果大多数是红色的（颜色特征）等等，当有足够多的同学对苹果进行了不同的描述后，这些描述合在一起就能充分的帮助不认识苹果的新同学来认识苹果。

关于AdaBoost的具体算法可以参考我的博文《机器学习技法总结（五）Adaptive Boosting, AdaBoost-Stump,决策树》和《机器学习技法实现（一）：AdaBoost- Decision Stump （AdaBoost - 决策树的基于Matlab的实现）》。

最后得到的实际上是一个决策树，每个树的节点都是一个决策树桩，很简单的弱分类器。关于决策树也可以参看上面的两篇博文，下面是引用维基百科的解释：

“机器学习中，决策树是一个预测模型；他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象，而每个分叉路径则代表的某个可能的属性值，而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出，若欲有复数输出，可以建立独立的决策树以处理不同输出。从数据产生决策树的机器学习技术叫做决策树学习,通俗说就是决策树。”（来自《维基百科》）

下面的这张图就是训练完毕的用于人脸检测识别的决策树：

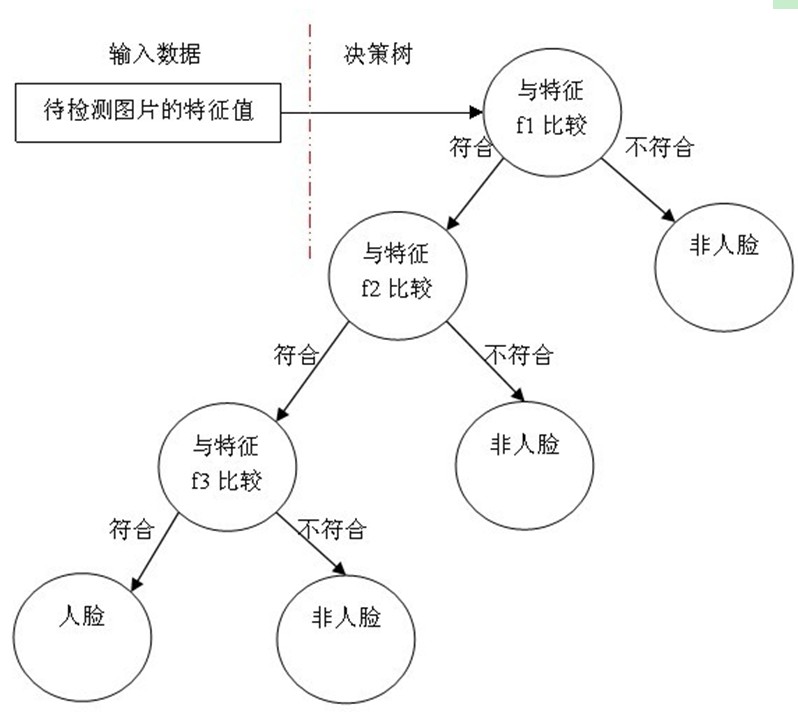
只有通过所有的决策树桩检测的才会被认定为人脸，就好像是只有满足所有同学对苹果的描述特点的东西，新同学才会认为它是苹果。

2015-9-23 艺少