python中的负数取模问题(一个大坑)
先来看一段代码
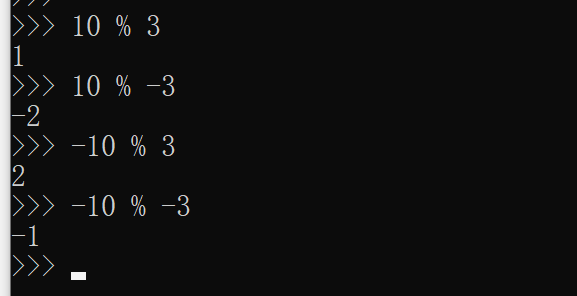
这是什么情况?为什么会出现这种结果。我们再来看看其它语言的执行结果


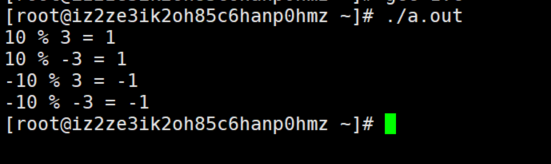
我们用golang、js、c分别算了一下,结果得到的结果都是一致的,但是python为啥不一样呢?
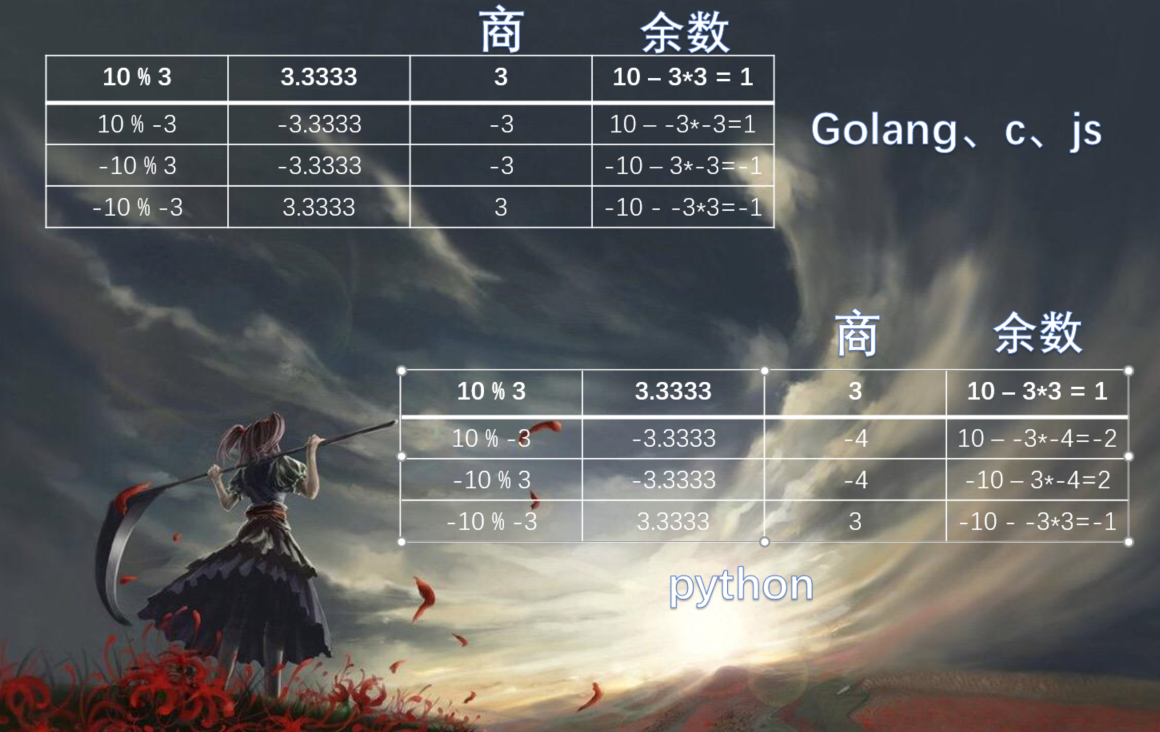
其实之所以这么做是python有意而为之,因为python对于正负号不同的两个值的除法处理方式和其它流行语言不一样。这就要考虑到机器是如何计算商和余数的,以10 % 3为例,先算10 / 3 = 3.333,然后取整得到3,也就是商,然后10 - 3 * 3=1,因此对于两个正数相除是没有疑问的,一样的结果。
但是如果是负数相除就不一样了,python是向下取整,而golang、c、js等语言则是直接把小数点后面截断,然后得到商。比如:10 % -3,得到-3.3333。如果是golang等其他语言,那么直接截断,因此商就是-3。10减去-3乘上-3,得到余数就是1。但如果是python,那么就向下取整,因此商是-4,所以10 - (-4 * -3)得到-2
python中的负数取模问题(一个大坑)的更多相关文章
- 【转】C/C++除法实现方式及负数取模详解
原帖:http://blog.csdn.net/sonydvd123/article/details/8245057 一.下面的题目你能全做对吗? 1.7/4=? 2.7/(-4)=? 3.7%4=? ...
- C++负数取模
预习: r=余数 a=被除数 b=除数 c=商 a/b=c........r r=a-(a/b)*b 一.下面的题目你能全做对吗?1.7/4=?2.7/(-4)=?3.7%4=?4.7%(-4)=?5 ...
- C/C++除法实现方式及负数取模详解
一.下面的题目你能全做对吗? 1.7/4=? 2.7/(-4)=? 3.7%4=? 4.7%(-4)=? 5.(-7)/4=? 6.(-7)%4=? 7.(-7)/(unsigned)4=? 答案: ...
- CodeForces 450B (矩阵快速幂模板题+负数取模)
题目链接:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=51919 题目大意:斐波那契数列推导.给定前f1,f2,推出指定第N ...
- python中的数字取整(ceil,floor,round)概念和用法
python中的数学运算函数(ceil,floor,round)的主要任务是截掉小数以后的位数.总体来说 就是取整用的.只是三者之间有微妙的区别: floor() :把数字变小 ceil() : ...
- python中如何不区分大小写的判断一个元素是否在一个列表中
python中判断某一个元素是否在一个列表中,可以使用关键字in 和 not in. 示例如下: 如果需要输出相应的信息,可以搭配使用if语句,这里不赘述. --------------------- ...
- python中如果函数后面有多于一个括号是怎么回事?
一般而言,调用一个函数是加一个括号.如果看见括号后还有一个括号,说明第一个函数返回了一个函数,如果后面还有括号,说明前面那个也返回了一个函数.以此类推. 比如fun()() def fun(): pr ...
- python中操作excel数据 封装成一个类
本文用python中openpyxl库,封装成excel数据的读写方法 from openpyxl import load_workbook from openpyxl.worksheet.works ...
- python中小数点后取2位(四舍五入)以及取2位(四舍五不入)
一.小数点后取2位(四舍五入)的方法方法一:round()函数其实这个方法不推荐大家使用,查询资料发现里面的坑其实很多,python2和python3里面的坑还不太一样,在此简单描述一下python3 ...
随机推荐
- Java各种反射性能对比
对各种方法实现get方法的性能进行了一个测试. 总共有5个测试,,每个测试都是执行1亿次 1. 直接通过Java的get方法 2.通过高性能的ReflectAsm库进行测试 3.通过Java Clas ...
- 在SSH里面远程启动ubuntu上的GUI程序
由于嵌入式开发板上是ubuntu系统,开发板接有显示器,现有一GUI程序需要在开发板显示器上实时显示,开发板与本地通过网络SSH连接,正常情况执行如:firefox,那么firefox会显示到本地,只 ...
- document.documentElement.clientHeight 和 document.body.clientHeight
document.documentElement.clientHeight 和 document.body.clientHeight 介绍 在进行一些网页效果处理的时候,经常碰到document.do ...
- vue中 keep-alive 组件的作用
原文地址 在vue项目中,难免会有列表页面或者搜索结果列表页面,点击某个结果之后,返回回来时,如果不对结果页面进行缓存,那么返回列表页面的时候会回到初始状态,但是我们想要的结果是返回时这个页面还是之前 ...
- 计蒜客 —— 字符串p型编码
给定一个完全由数字字符('0','1','2',…,'9')构成的字符串 strstr,请写出 strstr 的 pp 型编码串. 例如:字符串122344111可被描述为“1个 1.2 个 2.1 ...
- JQ scrollTop 无效的场景
先要设置DOM为显示,然后在设置scrollTop,先后顺序不能调换.
- [转帖]中芯国际14nm秋季量产 7nm工艺或在2020年底问世
中芯国际14nm秋季量产 7nm工艺或在2020年底问世 https://news.mydrivers.com/1/641/641087.htm 中芯正在发力.. 今年秋天 14nm两场 明年底 7n ...
- SQL SERVER DATENAME函数
定义: DATENAME函数返回指定日期的指定部分. 语法: DATENAME(datepart,date) 参数: ①datepart 参数可以是下列的值: datepart 缩写 年(Year) ...
- python报错及处理 -- 不断总结
ModuleNotFoundError: No module named 'PIL' 解决方法: 运行命令:pip install Pillow IndentationError: expected ...
- linux下vi编辑器常用命令
最近折腾云主机centOS,不得不接触到各种命令,特别是vi编辑器. 时常悔恨当时没好好听金老伯的linux课,导致现在操作命令用的十分生疏,甚至跳转行首行尾都要查一查才知道. 所以〒▽〒有了下面这篇 ...
