588 div2 C. Anadi and Domino

C. Anadi and Domino

题目链接：https://codeforces.com/contest/1230/problem/C

Anadi has a set of dominoes. Every domino has two parts, and each part contains some dots. For every aa and bb such that 1≤a≤b≤61≤a≤b≤6, there is exactly one domino with aa dots on one half and bb dots on the other half. The set contains exactly 2121 dominoes. Here is an exact illustration of his set:

Also, Anadi has an undirected graph without self-loops and multiple edges. He wants to choose some dominoes and place them on the edges of this graph. He can use at most one domino of each type. Each edge can fit at most one domino. It's not necessary to place a domino on each edge of the graph.

When placing a domino on an edge, he also chooses its direction. In other words, one half of any placed domino must be directed toward one of the endpoints of the edge and the other half must be directed toward the other endpoint. There's a catch: if there are multiple halves of dominoes directed toward the same vertex, each of these halves must contain the same number of dots.

How many dominoes at most can Anadi place on the edges of his graph?

Input

The first line contains two integers nn and mm (1≤n≤71≤n≤7, 0≤m≤n⋅(n−1)20≤m≤n⋅(n−1)2) — the number of vertices and the number of edges in the graph.

The next mm lines contain two integers each. Integers in the ii-th line are aiai and bibi (1≤a,b≤n1≤a,b≤n, a≠ba≠b) and denote that there is an edge which connects vertices aiai and bibi.

The graph might be disconnected. It's however guaranteed that the graph doesn't contain any self-loops, and that there is at most one edge between any pair of vertices.

Output

Output one integer which denotes the maximum number of dominoes which Anadi can place on the edges of the graph.

 

Note

Here is an illustration of Anadi's graph from the first sample test:

And here is one of the ways to place a domino on each of its edges:

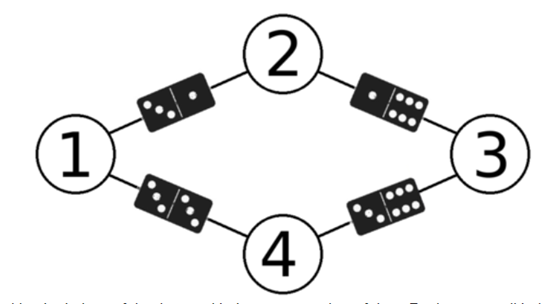
Note that each vertex is faced by the halves of dominoes with the same number of dots. For instance, all halves directed toward vertex 11have three dots.

题意：每个指向顶点的点数是相同的，且每个骰子不能重复使用，问最多有几条边可以被摆放，其中可以用相同的点数指向不同的顶点

题解：如果顶点数小于等于6的话，肯定每个边都可以摆放。

那只要考虑有七个顶点的情况，肯定有一个点数是被两个顶点共用，如果这两个顶点还连接同一个顶点时，由于每个骰子只能使用一次，这两个边中肯定会有其中一条边被舍弃，所以枚举每两个顶点，有几个指向同一个顶点的就删去几个，找到最少的删除边，把其减去就是答案。

代码：

 #include <iostream>
 #include <algorithm>
 #include <cstdio>
 #include<vector>
 #include<string.h>
 #include<queue>
 #include<map>
 #include<math.h>
 #include<stdio.h>
 #define inf 0x3f3f3f
 #define ll long long
 using namespace std;
 int a[][]={};
 int main()
 {
     int n,m;
     cin>>n>>m;
     for(int i=;i<=m;i++)
     {
         int p,q;
         cin>>p>>q;
         a[p][q]=a[q][p]=;
     }int ans=inf,t;
     if(n<=)
     {
         cout<<m<<endl;
         return ;
     }
     else
     {
         for(int i=;i<;i++)
         {
             for(int j=i+;j<=;j++)
             {
                 t=;
                 for(int k=;k<=;k++)
                 {
 
                     if(a[i][k]&&a[j][k])
                     {
                         t++;
                     }
                 }
                 ans=min(ans,t);
             }
         }
         cout<<m-ans<<endl;
     }
     return ;
 }