问题 A: 雷神领域

传送门

题目描述

L君，S大陆首屈一指的天才魔法师，创造了一个新魔法：雷神领域。  
这个魔法会首先在地面上形成正方网格魔法阵列，然后在某些位置召唤雷电轴标。注意：一个位置只能有一个雷电轴标存在。 
雷电轴标总出现在正方网格魔法阵列的顶点处，所以我们可以用一个有序整数对(X_i,Y_i)标记它的位置。  
然后，如果存在三个雷电轴标A,B,C满足：XA=XB, YA=YC，则该魔法会立即召唤一个位置在(XC,YB)的雷电轴标，如此往复直至不存在满足条件的雷电轴标组为止。  
最后，L君将选择一条正方网格魔法阵列上的路径并使用自然力激活它们，这时候雷神领域的魔法强度就被定义为路径上的雷电轴标所占用的行数中或者列数中的较小值。 
但是由于L君才刚创造这个魔法，如果选择的路径中出现U形或往返子路径，那么会给施展魔法的魔法师带来一定危险性。所以选择的路径不应该包含U形子路径或往返子路径。（类似 |__ __ __| 这样的广义U形路径也不行）  
由于自然力必须从魔法师的体内调和，所以路径的起点应该是魔法师所站的位置，即正方网格魔法阵列的左下角(0,0)点。  
现在他想要询问你——以扫地为生来隐藏自己真实身份的大陆有史以来最伟大的式神制造师Lwins_***，他所能释放的雷神领域的最高魔法强度。 
当然，路径由你来为他选择。虽然如此，作为一个魔法天才，其实他只关心最高魔法强度而已。 

输入

第1行:包含一个正整数N，表示接下来的数据个数。  
接下来N行:每行包含两个正整数Xi,Yi，表示(Xi,Yi)处存在一个雷电轴标。

---

对于30%的数据：N≤10, 0＜Xi,Yi≤5。  
对于60%的数据：0＜Xi,Yi≤2000。  
对于100%的数据：N≤15000, 0＜Xi,Yi≤5000 

输出

包含一行，为可能的最高魔法强度。

样例输入 Copy

7
1 1
1 1
1 1
1 2
1 3
2 2
3 1

样例输出 Copy

　　3

考试时的心理历程

• 记得很早以前，老师好像说过什么题目难度和顺序无关，然后就看到第一题又是红字又是加粗还有斜体，第一反应就是这不是人做的。。。　　
• 然后去看了一下第二题，第一反应就是一个搜索，然后就发现竟然还有什么传送门，那传送出去之后不还在门上吗，那岂不是永远出不来了？，就随便打了一个最简单的搜索，没看门，竟然还拿了10分。。。
• 第三题就是毒瘤，题面简单明了，思路也是短小精悍，不会。。。然后开了一个10000*10000的数组不但没爆还拿了10分。。。

第一题的缩小版：

　　在一个5000*5000的矩阵里，已知n对（x，y），表示在（x，y）有一个雷神标记，若Xa==Xb并且Ya==Yc则（Xc，Yb）处也会产生一个雷神标记，最后他有一定限制的走，问最大的长或宽是多少

第一题思路：

　　一开始乱搞了一个半小时没往正解上去想，然后就看出来了是冰茶姬，而这题的关键就在于怎么把扩展出来的点找出来，至于DP什么的就很水，同样是DP蓝题，和那个妙题包里的根本不在一个档次。。。然后考场上ZYM大佬亲自尝试N²的解法然后就T掉了，回家一路上都在纠结于N²的算法，然后我才想起来哪儿错的。。。。其实这很简单

• 把行和列分别看成N个点，就形成了一个N*N的点阵。
• 因为X是1-->maxn，Y也是1--->maxn，所以为了避免重复，Y可以用maxn+1----->maxn+maxn来表示，parent数组要开两倍，不然运气好会有50分，运气不好就不知道会不会有分了。。。
• 然后举个栗子：假设有我们知道三个点（1,5001），（1,5002），（2,5002）然后画成图就是这样

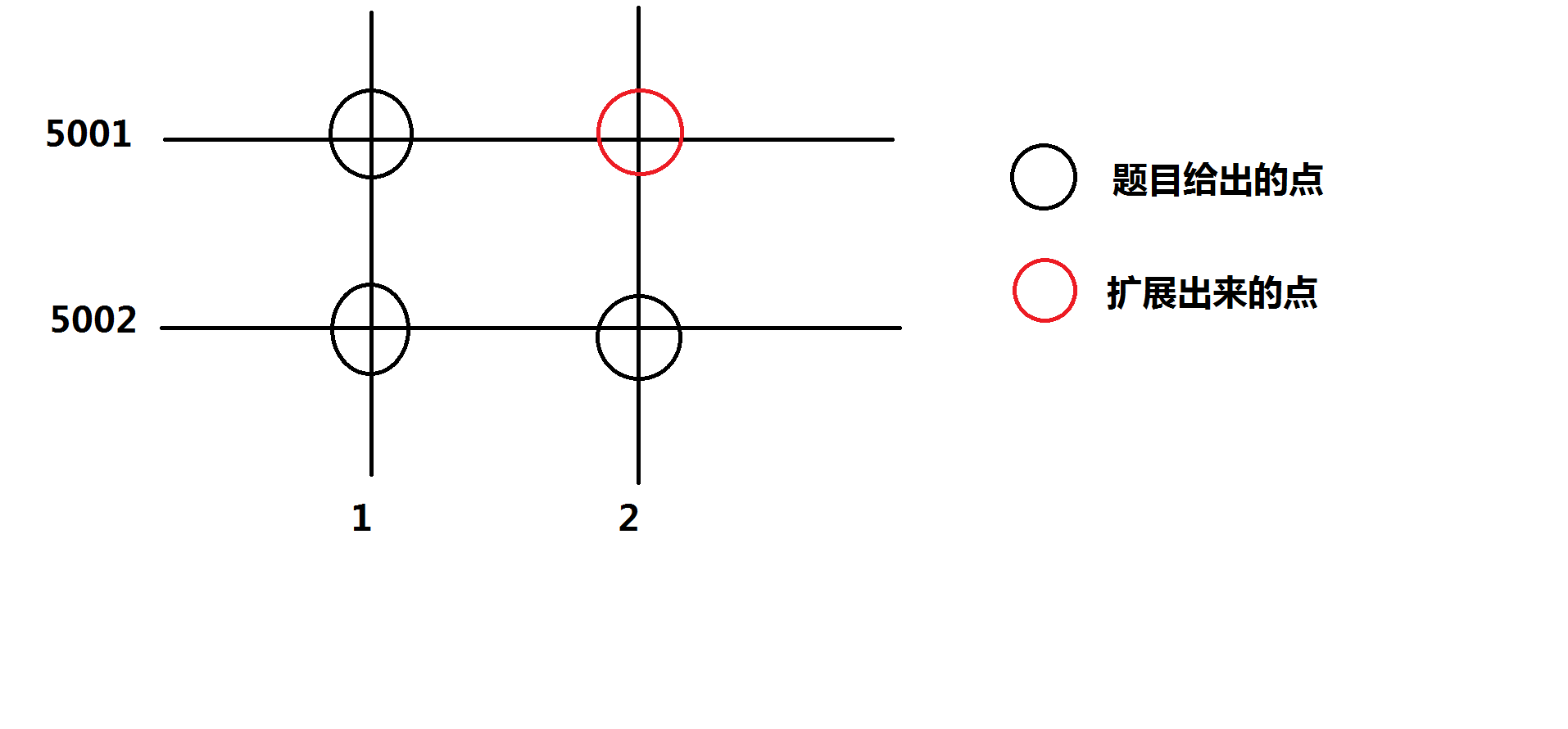
然后把所有点的坐标都列出来（1,5001）（1,5002）（2,5002）----->（2,5001），仔细一数好像每个数字都出现了俩次，然后如果把每个给定点的坐标都放到一个集合里就可以发现有这么一个集合{1,5001,2,5002}，然后把集合里的数排列一下，小于5000的当X，大于5000的当Y，会发现有四个坐标，其中三个是我们已知的，而另外一个就是我扩展出来的点的坐标。

　　再举个栗子

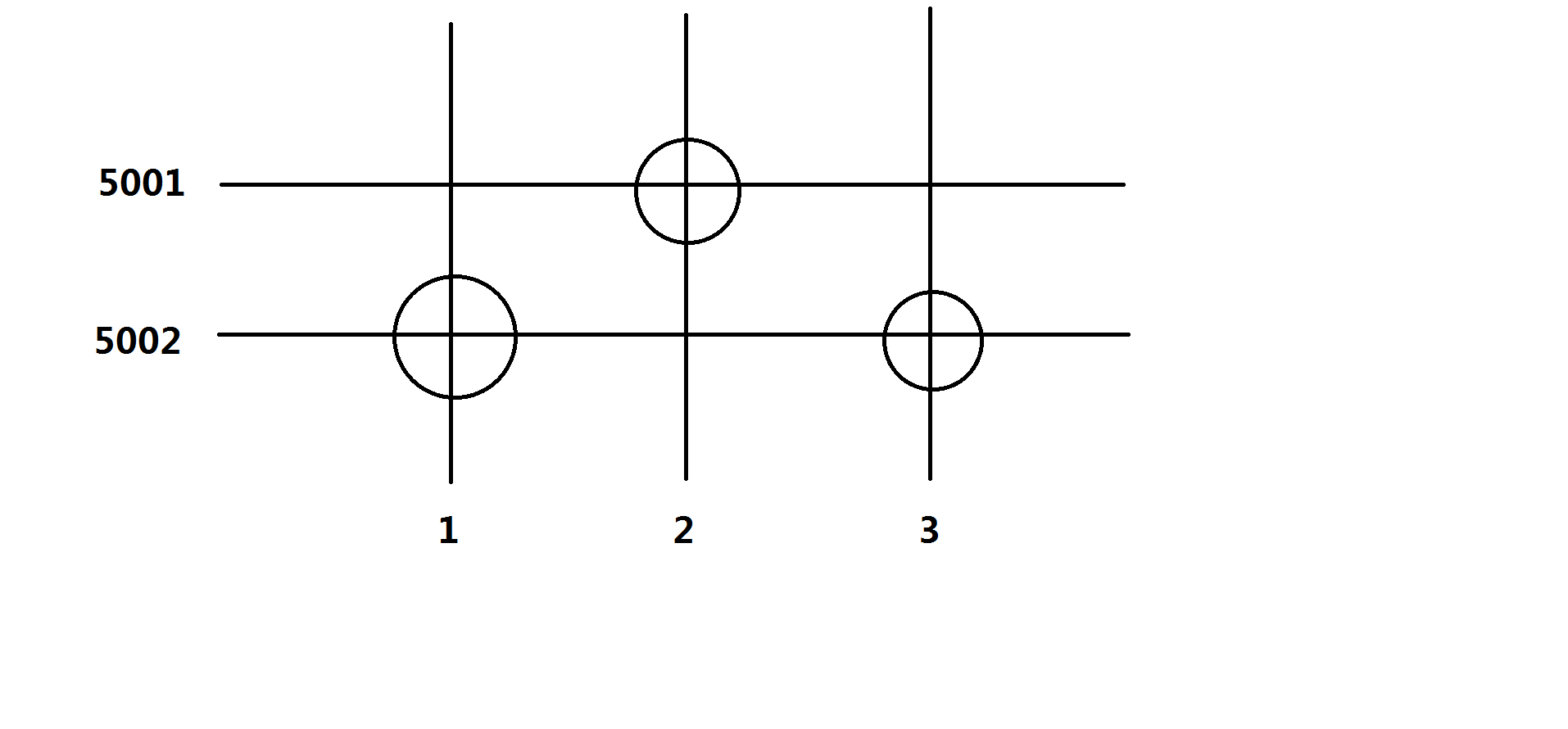
　　对于上面这个图，可以形成{2,5001}和{1,5002,3}两个集合，然而拆开之后就会发现最多只会形成3个点，没有新的点就意味着没有可以扩展出来的新点。

　　至于为什么一定要用冰茶姬，这个也不一定，只要能把坐标放到一个集合里都可以，大佬们也可以尝试其他算法，用它主要还是因为是无向的，判断联通也很方便，简而言之，就是因为太懒了。。。

• 由此我们可以得出结论只要把他给的点都放到一个集合中，然后在之后对整个矩阵遍历的时候判断i和j在不在同一个集合里，如果在一个集合里就会有一个标记，反之亦然。
• 然后就可以在5000*5000的矩阵里面跑DP，感觉DP也很好想。F【i】【j】表示从原点到（i，j）时的答案。
• 如果I和J在同一个集合里，说明这个地方有一个标记，此时F【i】【j】=F【i-1】【j-1】+1；因为无论是行还是列从-1传到这里是他最后的答案都要+1；
• 如果I和J不在同一个集合中，那说明此处没有标记，那此时F【i】【j】=max（F【i-1】【j】，F【i】【j-1】）；从上面的一次中无论是行还是列取一个最大值继承到当前点。
• 最后的答案就是F【maxn】【maxn】。

代码同样也很短：

 #include<bits/stdc++.h>
 using namespace std;
 inline int read()
 {
     int x=,f=;char c=getchar();
     for(;!isdigit(c);c=getchar()) if(c=='-') f=-;
     for(;isdigit(c);c=getchar()) x=x*+c-'';
     return x*f;
 }
 const int maxn=;
 int parents[maxn*+],f[maxn+][maxn+];
 inline int find(int x) {return parents[x]==x?x:parents[x]=find(parents[x]);}
 int main()
 {
     int n=read();
     for(int i=;i<=;i++) parents[i]=i;
     for(int i=;i<=n;i++)
     {
         int x=read(),y=read();
         parents[find(x)]=find(y+maxn);
     }
     for(int i=;i<=maxn;i++)
     {
         for(int j=;j<=maxn;j++)
         {
             if(find(i)==find(j+maxn))
             {
                 f[i][j]=f[i-][j-]+;
              }
             else
             {
                 f[i][j]=max(f[i][j-],f[i-][j]);
             }

         }
     }
     printf("%d\n",f[maxn][maxn]);
     return ;
 }