基于canvas二次贝塞尔曲线绘制鲜花

canvas中二次贝塞尔曲线参数说明：

• cp1x:控制点1横坐标
• cp1y:控制点1纵坐标
• x: 结束点1横坐标
• y:结束点1纵坐标
• cp2x:控制点2横坐标
• cp2y:控制点2纵坐标
• z:结束点2横坐标
• y:结束点2纵坐标

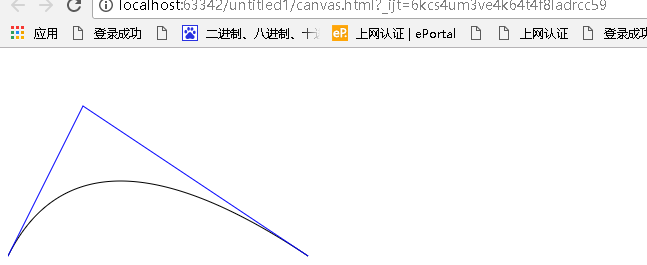
示例效果图如下：

示例代码如下：

var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');
var width = 0;
var height = 0;
var centerX = 0;
var centerY = 0;
var num = 6;
var maxSize = 200;
var flowerBranch = 300;
var range = 0;
var rangeType = 'up';
var grassNum = 1200;
var grassHeight = 50;
var grassArray = [];
var randomArray = [];
var petalArray = [];
getGrassArray();
draw();
function draw() {
      width = $('body').innerWidth();
      height = $('body').innerHeight();
      ctx.clearRect(0,0,width,height);
      centerX = width / 2 + range;
      centerY = height / 2 - flowerBranch / 2 + maxSize / 2 + Math.abs(range) / 5;
      canvas.width = width;
      canvas.height = height;
      drawFlowerBranch();
      drawFlowerSide();
      drawFlower(centerX,centerY,maxSize,'#ff0000');
      drawFlower(centerX,centerY,maxSize * 0.8,'#000000');
      drawFlower(centerX,centerY,maxSize * 0.6,'#ccc');
      drawFlowerCenter(maxSize * 0.2);
      drawGrass();
      if (range >= 20) {
          rangeType = 'down';
        petalArray.push({
              type: 'right',
              x: centerX,
              y: centerY,
              size: Math.random() * 100,
             color: 'rgb(' + parseInt(Math.random() * 255) + ',' + parseInt(Math.random() * 255) + ',' + parseInt(Math.random() * 255) + ')'
        });
     }
      if (range <= -20) {
          rangeType = 'up';
        petalArray.push({
              type: 'left',
              x: centerX,
              y: centerY,
              size: Math.random() * 100,
              color: 'rgb(' + parseInt(Math.random() * 255) + ',' + parseInt(Math.random() * 255) + ',' + parseInt(Math.random() * 255) + ')'
        });
    }
      if (rangeType == 'down') {
          range -= 0.4;
    } else {
        range += 0.4;
       }
      requestAnimationFrame(draw);
}
function drawFlowerBranch () {
      ctx.beginPath();
      ctx.fillStyle = '#b89909';
      ctx.moveTo(centerX,centerY);
      ctx.quadraticCurveTo(centerX + 25, (height + centerY) / 2,width / 2,height);
      ctx.lineTo(width / 2 - 20,height);
      ctx.quadraticCurveTo(centerX + 5, (height + centerY) / 2,centerX,centerY);
      ctx.fill();
}
function drawFlowerSide() {
      var _petalArray = [];
      petalArray.forEach(function (item) {
        if (item.type == 'left') {
            if (item.x > 0 || item.y < height) {
                  _petalArray.push(item)
            }
              item.x -= Math.random();
              item.y += Math.random();
              drawFlower(item.x,item.y,item.size,item.color);
        }
        if (item.type == 'right') {
            if (item.x < width || item.y < height) {
                  _petalArray.push(item)
            }
              item.x += Math.random();
              item.y += Math.random();
              drawFlower(item.x,item.y,item.size,item.color);
        }
      })
      petalArray = _petalArray;
}
function drawFlower(centerX,centerY,size,color) {
      for(var i = 0; i < num; i ++) {
        drawPetal(centerX,centerY,360 / num * i,size,color);
      }
}
function drawPetal(centerX,centerY,deg,size,color) {
      ctx.save();
      ctx.translate(centerX,centerY);
      ctx.fillStyle = color;
      ctx.beginPath();
      ctx.moveTo(0,0);
      ctx.rotate(Math.PI / 180 * deg);
      ctx.quadraticCurveTo(size / 2, -size / 4, size, 0);
      ctx.quadraticCurveTo(size / 2, size / 4, 0, 0);
      ctx.fill();
      ctx.restore();
}
function drawFlowerCenter(size){
      ctx.beginPath();
      ctx.fillStyle = '#edf01a';
      ctx.moveTo(centerX,centerY);
      ctx.arc(centerX,centerY,size,0,Math.PI * 2);
      ctx.fill();
      for (var i = size - 5; i > 0; i -= 8) {
        ctx.beginPath();
        ctx.strokeStyle = '#ff0000';
        ctx.moveTo(centerX,centerY);
        ctx.setLineDash([1,10]);
        ctx.linCap = 'round';
        ctx.arc(centerX,centerY,i,0,Math.PI * 2);
        ctx.stroke();
      }
}
function getGrassArray () {
      width = $('body').innerWidth();
      for (var i = 0; i < grassNum; i ++) {
        grassArray.push(Math.random() * width);
        randomArray.push(Math.random() * 3);
      }
}
function drawGrass() {
      for (var i = 0; i < grassNum; i ++) {
        var random = randomArray[i];
        var grassX = grassArray[i];
        ctx.fillStyle = '#0bad35';
        ctx.beginPath();
        ctx.moveTo(grassX,height);
        ctx.quadraticCurveTo(grassX + 5 + range * 0.4, height - grassHeight * random / 2, grassX + range * 0.4, height - grassHeight * random);
        ctx.quadraticCurveTo(grassX + 3 + range * 0.4, height - grassHeight * random / 2, grassX - 3, height);
        ctx.fill();
      }
}

示例代码下载地址：基于canvas二次贝塞尔曲线绘制鲜花