洛谷P4015 运输问题 网络流24题

看了下SPFA题解，一个一个太麻烦了，另一个写的很不清楚，而且注释都变成了"????"不知道怎么过的，于是自己来一发SPFA算法。

Part 1.题意

M 个仓库，卖给 N 个商店，两个问，第一问求运价最小值，第二问最大值。

显然是一个最小费用最大流(MCMF)。

Part 2.思路

1.连让每个仓库连接一个超级源点 SS ，费用(dis)为0，流量为仓库的流量，表示每个仓库最多可以运出多少货物。

2.让每一个仓库连接每一家商店，边权为 cost[i][j] ，其中，i为仓库编号，j为商店编号编号，流量为 need[j] ，其实流量可以取得范围是  [need[j]...INF] ，另外如果出现 need[j] <这个仓库货物量的情况也可以不怕(这时候取值的下限变成 min(hw[i],need[j]) ) hw指的是这家仓库的货物，还有注意编号的范围（我默认超级源点是 00 ，仓库是 1……n ,商店是 n+1……n+m ，超级汇点是 10000）

3.让每一家商店连接超级汇点 TT

图像帮助理解：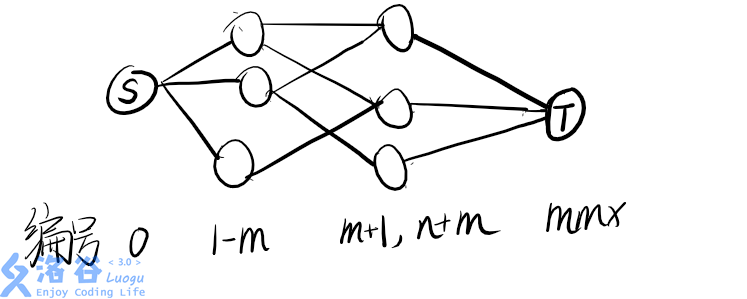 

Part 3.代码

现在代码就好办了 注释给的很清楚

 #include<iostream>
 #include<cmath>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 #include<stack>
 #include<vector>
 #include<map>
 #include<set>
 #include<algorithm>

 #define I_copy_this_answer return 0;

 using namespace std;

 int n,m,head[],size=;
 int mmx=,mincost,maxwater;
 int flow[];
 int need[],cost[][];
 int pre[],las[],dis[],vis[],hw[];

 struct edge{
     int next,to,dis,flow;
 }e[]; 

 void addedge(int next,int to,int dis,int flow)
 {
     e[++size].to=to;
     e[size].dis=dis;
     e[size].flow=flow;
     e[size].next=head[next];
     head[next]=size;
 }

 int spfa(int s)
 {
     memset(flow,0x3f,sizeof(flow));
     memset(dis,0x3f,sizeof(dis));
     memset(vis,,sizeof(vis));
     queue <int> q;
     q.push(s);
     dis[s]=;
     vis[s]=;
     pre[mmx]=-;  //（其实只要不是与p直接连的点(n+1......n+m)就可以了
     while(!q.empty())
     {
         int t=q.front();
         q.pop();
         vis[t]=;
         int i,j,k,l;
         for(i=head[t];i;i=e[i].next)
         {
             j=e[i].to;
             k=e[i].dis;
             l=e[i].flow;
             if(dis[t]+k<dis[j]&&l>)  //没有流量的话这条路就增广不了，最短距离是建立在增广路存在的基础上的
             {
                 dis[j]=dis[t]+k;
                 las[j]=i;  //las指的是这个点(j)与上个点(t)相连的边的编号
                 pre[j]=t;  //pre指的是这条路径上这个点(j)的上一个点
                 flow[j]=min(flow[t],l);  //把当前边流量与上个点的流量对比，解决出现仓库货物比需要的少的情况
                 if(!vis[j])
                 {
                     q.push(j);
                     vis[j]=;
                 }
             }
         }
     }
     return pre[mmx]!=-;  //如果不是这个值就说明这个点被刷新，增广成功
 }

 void mcmf()
 {
     while(spfa())
     {
         mincost+=dis[mmx]*flow[mmx];   //从源点出发到汇点的单位费用再乘以单位，由于每次只增广一条路，而且仓库和商店是直接连接的，可以这样写
         int t=mmx;
         while(t!=)
         {
             e[las[t]].flow-=flow[mmx];  //回溯，修改每条边的流量，因为该算法中途找到的增广路不是最后的增广路，所以这个要等到最后来改变
             e[las[t]^].flow+=flow[mmx];
             t=pre[t];
         }
     }
 }

 void build_edge(int t)
 {
     int i,j;
     for(i=;i<=m;i++)
     {
         addedge(,i,,hw[i]);
         addedge(i,,,);
     }
     for(i=;i<=m;i++)
     for(j=;j<=n;j++)
     {
         addedge(i,j+m,cost[i][j]*t,need[j]);
         addedge(j+m,i,-cost[i][j]*t,);
     }
     for(i=;i<=n;i++)
     {
         addedge(i+m,mmx,,need[i]);
         addedge(mmx,i+m,,);
     }
 }

 int main()
 {
     int i,j;
     scanf("%d %d",&m,&n);
     for(i=;i<=m;i++)
     {
         int t1;
         scanf("%d",&hw[i]);
     }
     for(i=;i<=n;i++)
         scanf("%d",&need[i]);
     for(i=;i<=m;i++)
     for(j=;j<=n;j++)
         scanf("%d",&cost[i][j]);  //读入，与上面的cost,need,hw如果不明白可以对照输入格式看代表什么意思
     build_edge();  //建立边权为正的边，跑最小费用最大流
     mcmf();//最小费用最大流(Min Cost Max Flow ）的缩写
     printf("%d",mincost);
     maxwater=;
     mincost=;
     size=;
     memset(head,,sizeof(head));
     build_edge(-);
     mcmf();
     printf("\n%d",-mincost);
     I_copy_this_answer
 }