不能走路（walk）

【题目背景】

小G 同学总是在树上走路。小S 看不下去了，决定阻止小G 同学。

【题目描述】

有一棵 n 个点的树，树上有 m 条路径，每条路径为 x[i]到y[i] 的树上最短路径（不经过相同的边），小 S 想要摧毁树上的 K 个点， 使得每一条路径上都有至少一个点被摧毁。

你只需要求出最小的K，而不用输出摧毁了哪些点。

数据点编号	n<=	m<=
1	15	15
2	100	15
3	100	15
4	100	100
5	1000	1000
6	5000	5000
7	5000	5000
8	100000	100000
9	100000	100000
10	100000	100000

【样例输入】

5 2

1 2

2 3

2 4

2 5

1 5

3 4

【样例输出】

1

【提示】

如果需要用到较大的栈空间。

可以在编译命令加上-Wl,--stack=2333333333。评测时开栈。

题解

受洛谷P1967 货车运输启发，这题很像LCA。

于是我们就尝试切LCA。

首先，不难发现阻断LCA是可行的，那么是最优的吗？

对于一颗子树内的点，如果从该子树的点要延伸出子树外，那必须经过最顶端的点。

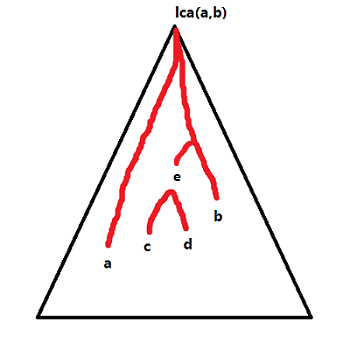
如图，对于一个点，若要与外面有联系，那必定要经过\(lca(a,b)\)。

那两点的联系在子树内呢？如果是\(c\to d\)，那显然是无关的，那\(e\to b\)呢？我们发现最优应该切\(lca(e, b)\)。

那不是就WA了吗？不。我们发现：如果我们先切\(lca(e, b)\)，到\(a\to b\)是特判一下即可。

由于数据很水，判是否联通用暴力爬就可以了。

下面上代码，刚学树剖，于是就打了个树剖。

#include <cstdio>
#include <algorithm>

using namespace std;

const int maxn = 100005;

struct Edge
{
	int to, nxt;
} e[maxn<<1];

int first[maxn];

int nowm;
inline void add_edge(int from, int to)
{
	e[++nowm].nxt = first[from];
	e[nowm].to = to;
	first[from] = nowm;
	e[++nowm].nxt = first[to];
	e[nowm].to = from;
	first[to] = nowm;
}

int fa[maxn], son[maxn], dep[maxn], val[maxn];

inline void dfs1(int x)//找重链，标记深度与父亲
{
	dep[x] = dep[fa[x]] + 1;
	val[x] = 1;
	for(int i = first[x], dd; i; i = e[i].nxt)
	{
		dd = e[i].to;
		if(dd == fa[x])
			continue;
		fa[dd] = x;
		dfs1(dd);
		val[x] += val[dd];
		if(!son[x] || val[dd] > val[son[x]])
			son[x] = dd;
	}
}

int top[maxn];

inline void dfs2(int x, int ff)//寻找重链的顶端
{
	top[x] = ff;
	if(son[x])
		dfs2(son[x], ff);
	for(int i = first[x], dd; i; i = e[i].nxt)
	{
		dd = e[i].to;
		if(dd != fa[x] && dd != son[x])
			dfs2(dd, dd);
	}
}

inline void init(int s)
{
	dfs1(s);
	dfs2(s, s);
}

inline int lca(int a, int b)
{
	while(top[a] != top[b])
	{
		if(dep[top[a]] >= dep[top[b]])
			a = fa[top[a]];
		else
			b = fa[top[b]];
	}
	return dep[a] < dep[b] ? a : b;
}

struct sxd
{
	int a, b, t;

	inline bool operator < (const sxd& other) const
	{
		return dep[t] > dep[other.t];
	}
} ask[maxn];

bool biao[maxn];

inline bool pan(int a, int b)
{
	for(; a != fa[b]; a = fa[a])
		if(biao[a])
			return true;
	return false;
}

int main()
{
	freopen("walk.in", "r", stdin);
	freopen("walk.out", "w", stdout);
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i = 1, f, t; i < n; ++i)
	{
		scanf("%d%d", &f, &t);
		add_edge(f, t);
	}
	init(1);
	for(int i = 1; i <= m; ++i)
	{
		scanf("%d%d", &ask[i].a, &ask[i].b);
		ask[i].t = lca(ask[i].a, ask[i].b);//树剖lca模板
	}
	sort(ask+1, ask+m+1);//将提问排序，从下往上阻断
	int ans = 0;
	for(int i = 1; i <= m; ++i)//暴力往上爬……（竟不会T，还是最优解）
	{
		if(pan(ask[i].a, ask[i].t) || pan(ask[i].b, ask[i].t))
			continue;
		ans++;
		biao[ask[i].t] = true;
	}
	printf("%d\n", ans);
	return 0;
}