「中山纪中集训省选组D4T1」折射伤害 高斯消元

题目描述

在一个游戏中有n个英雄，初始时每个英雄受到数值为ai的伤害，每个英雄都有一个技能“折射”，即减少自己受到的伤害，并将这部分伤害分摊给其他人。对于每个折射关系，我们用数对\((x_i,y_i,z_i)\)来表示\(x_i\)将自己受到伤害去掉\(z_i\)的比例，将这些伤害转移给\(y_i\)（\(x_i,y_i\)是整数，\(z_i\)是实数）。

求出经过反复折射后最后每个英雄受到的实际总伤害。

输入格式

第一行一个正整数：\(n\)，表示有\(n\)个英雄，第二行\(n\)个整数\(A_i\)，依次表示每个英雄受到的初始伤害。第三行一个正整数\(m\)，表示有\(m\)对折射关系。接下来\(m\)行，每行三个数\(x_i,y_i,z_i\)，表示\(x_i\)将自己受到伤害去掉\(z_i\)的比例，将这些伤害转移给\(y_i\)。

输出格式

输出\(n\)行，第\(i\)行表示第\(i\)个英雄最后受到的实际总伤害。保留六位小数。

样例

样例输入

3
1 0 2
3
1 2 0.3000
1 2 0.2000
2 1 0.5000

样例输出

0.666667
0.333333
2.000000

数据范围

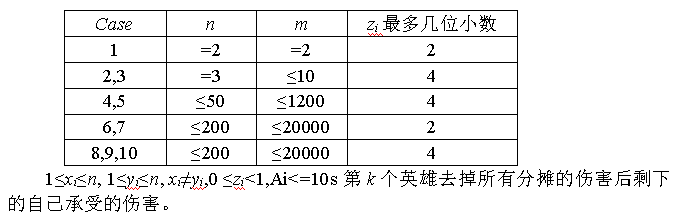
题解

设\(D_i\)为分摊伤害后\(i\)最终受到的伤害，\(C_i\)为\(i\)自己真实受到的的伤害占总伤害的比例，\(T_{i,j}\)表示\(i\)总共分给\(j\)的伤害的比例。

那么\(D_i\)中除了第一次天降的伤害\(A_i\)，其他伤害都是来源于别人的分摊，那么可以很轻松地推出一个式子：

\[\frac{D_i}{C_i}=\sum_{j≠i}\frac{D_j}{C_j}\cdot T_{j,i}+A_i
\]

直接按照这个式子建立关于\(D_i\)的方程组，然后高斯消元解方程即可。

\(Code:\)

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define N 205
#define M 20005
#define eps 1e-6
int n, m, A[N];
long double val[N][N], mat[N][N];
long double ans[N];
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		scanf("%d", &A[i]), val[i][i] = 1;
	int x, y;
	double c;
	scanf("%d", &m);
	for (int i = 1; i <= m; i++)
	{
		scanf("%d%d%lf", &x, &y, &c);
		val[x][y] += c;
		val[x][x] -= c;
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= n; j++)
			if (i != j)
				mat[i][j] = -val[j][i] / val[j][j];
		mat[i][i] = 1 / val[i][i];
		mat[i][n + 1] = -A[i];
	}
	for (int i = 1; i <= n; i++)
	{
		for (int j = i + 1; j <= n; j++)
			if (fabs(mat[j][i]) > eps)
			{
				for (int k = i; k <= n + 1; k++)
					swap(mat[i][k], mat[j][k]);
				break;
			}
		long double s = mat[i][i];
		for (int j = i; j <= n + 1; j++)
			mat[i][j] /= s;
		for (int j = i + 1; j <= n; j++)
		{
			s = mat[j][i];
			for (int k = i; k <= n + 1; k++)
				mat[j][k] -= s * mat[i][k];
		}
	}
	ans[n + 1] = 1;
	for (int i = n; i >= 1; i--)
		for (int j = i + 1; j <= n + 1; j++)
			ans[i] -= mat[i][j] * ans[j];
	for (int i = 1; i <= n; i++)
		printf("%.6lf\n", double(ans[i]));
}