LGOJ P2048 [NOI2010]超级钢琴

题目描述

小Z是一个小有名气的钢琴家，最近C博士送给了小Z一架超级钢琴，小Z希望能够用这架钢琴创作出世界上最美妙的音乐。

这架超级钢琴可以弹奏出n个音符，编号为1至n。第i个音符的美妙度为Ai，其中Ai可正可负。

一个“超级和弦”由若干个编号连续的音符组成，包含的音符个数不少于L且不多于R。我们定义超级和弦的美妙度为其包含的所有音符的美妙度之和。两个超级和弦被认为是相同的，当且仅当这两个超级和弦所包含的音符集合是相同的。

小Z决定创作一首由k个超级和弦组成的乐曲，为了使得乐曲更加动听，小Z要求该乐曲由k个不同的超级和弦组成。我们定义一首乐曲的美妙度为其所包含的所有超级和弦的美妙度之和。小Z想知道他能够创作出来的乐曲美妙度最大值是多少。

输入输出格式

输入格式：

输入第一行包含四个正整数n, k, L, R。其中n为音符的个数，k为乐曲所包含的超级和弦个数，L和R分别是超级和弦所包含音符个数的下限和上限。

接下来n行，每行包含一个整数Ai，表示按编号从小到大每个音符的美妙度。

输出格式：

输出只有一个整数，表示乐曲美妙度的最大值。

输入输出样例

输入样例#1：

复制

4 3 2 3
3
2
-6
8

输出样例#1：

复制

11

说明

共有5种不同的超级和弦：

1.    音符1 ~ 2，美妙度为3 + 2 = 5
2.    音符2 ~ 3，美妙度为2 + (-6) = -4
3.    音符3 ~ 4，美妙度为(-6) + 8 = 2
4.    音符1 ~ 3，美妙度为3 + 2 + (-6) = -1
5.    音符2 ~ 4，美妙度为2 + (-6) + 8 = 4

最优方案为：乐曲由和弦1，和弦3，和弦5组成，美妙度为5 + 2 + 4 = 11。

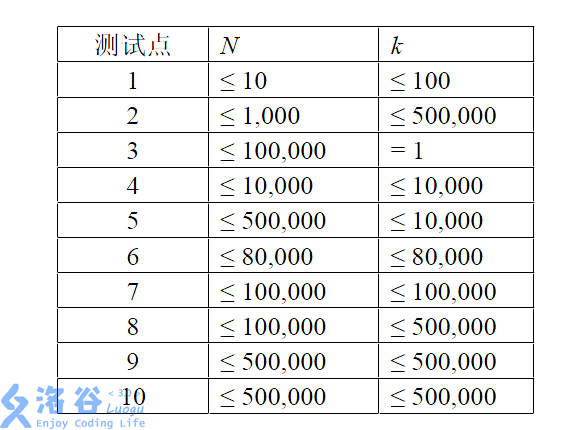
所有数据满足：-1000 ≤ Ai ≤ 1000，1 ≤ L ≤ R ≤ n且保证一定存在满足要求的乐曲。

题解

很有意思的一个题目。虽然没看题解我没想出来...

固定右端点，那么合法左端点就是连续的一段区间，子段和可以转换成前缀和相减的形式，那么就变成了在一段区间中求\(min\)的操作。这个用\(ST\)表维护。

用堆维护四元组\((val,id,l,r)\)(\(val\)区间最优答案，\(id\)为右端点的编号，\(l\)，\(r\)为合法左端点的区间)。按照\(val\)为关键字放进大根堆里面。

那么只要每次取出堆顶累计答案，找出使答案最大化的那个合法左端点x，再放\((newval_1,id,l,x)\)和\((newval_2,id,x+1,r)\)进去堆里就好了。

复杂度是\(O(n\log n)\)的

#include <bits/stdc++.h>
using namespace std;

namespace io {
char buf[1<<21], *p1 = buf, *p2 = buf;
inline char gc() {
    if(p1 != p2) return *p1++;
    p1 = buf;
    p2 = p1 + fread(buf, 1, 1 << 21, stdin);
    return p1 == p2 ? EOF : *p1++;
}
#define G gc

#ifndef ONLINE_JUDGE
#undef G
#define G getchar
#endif

#define I int
inline I read() {
    I x = 0, f = 1; char c = G();
    while(c < '0' || c > '9') {if(c == '-') f = -1; c = G(); }
    while(c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = G(); }
    return x * f;
}

inline void write(I x) {
    if(x == 0) {putchar('0'); return;}
    I tmp = x > 0 ? x : -x;
    if(x < 0) putchar('-');
    int cnt = 0;
    while(tmp > 0) {
        buf[cnt++] = tmp % 10 + '0';
        tmp /= 10;
    }
    while(cnt > 0) putchar(buf[--cnt]);
}
#undef I

#define in(x) x = read()
#define outn(x) write(x), putchar('\n')
#define out(x) write(x), putchar(' ')

} using namespace io;

#define ll long long
const int N = 500010;
const int inf = 1e9;

int n = read(), k = read(), L = read(), R = read();
ll s[N];
int a[N], lg[N];

struct node {
    ll v;
    int id;
}f[N][21];

struct task {
    int id, l, r;
};

node query(int l, int r) {
    int K = lg[r - l + 1];
    if(f[l][K].v > f[r - (1 << K) + 1][K].v) return f[r - (1 << K) + 1][K];
    return f[l][K];
}

bool operator < (task a, task b) {
    node v1 = query(a.l, a.r), v2 = query(b.l, b.r);
    return s[a.id] - v1.v < s[b.id] - v2.v;
}

priority_queue<task>q;

void init() {
    for(int i = 1; i <= n; ++i) {
        in(a[i]);
        s[i] = s[i - 1] + a[i];
        f[i][0].v = s[i];
        f[i][0].id = i;
    }
    for(int i = 2; i <= n; ++i) lg[i] = lg[i / 2] + 1;
    for(int j = 1; (1 << j) <= n; ++j) {
        for(int i = 0; i <= n; ++i) {
            if(i + (1 << j) - 1 > n) break;
            if(f[i][j - 1].v > f[i + (1 << (j - 1))][j - 1].v) f[i][j] = f[i + (1 << (j - 1))][j - 1];
            else f[i][j] = f[i][j - 1];
        }
    }
    for(int i = L; i <= n; ++i) {
        q.push({i, max(i - R, 0), i - L});
    }
}

int main() {
    init();

    ll ans = 0;
    while(k--) {
        task now = q.top(); q.pop();
        node x = query(now.l, now.r);
        ans += s[now.id] - s[x.id];
        if(now.l != x.id) q.push({now.id, now.l, x.id - 1});
        if(x.id != now.r) q.push({now.id, x.id + 1, now.r});
    }

    printf("%lld\n", ans);
}