实力封装：Unity打包AssetBundle（番外篇）

前情提要：第二种打包方式。

自定义AssetBundle包扩展名

在之前的教程中，我们已经多次提到过扩展名了，并且也已经说明了如何设置自定义的AssetBundle扩展名。至于为什么还要把它单独拿出来说一遍，自然是有它的道理的，因为这里面有一个巨大的坑...

注意，前方有坑。。。

根据前面的剧情，我们有三方式可以设置自定义的AssetBundle包扩展名，下面就来一一讲解：

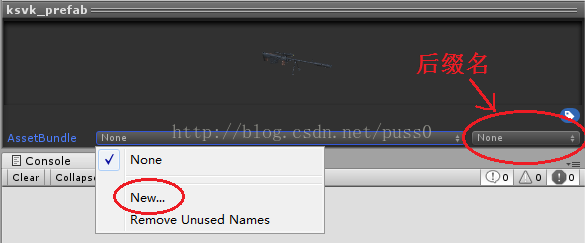
一、在Inspector面板中设置扩展名

这种设置AssertBundle包扩展名的方式可能是最简单的方式了，这里我把图片再放一遍↓↓

使用这种方式设置扩展名也有坑的地方，据我的尝试，也不是任意的扩展名都可以的，假如通过这种方式设置了扩展名，但是打包以后却没有看到扩展名，那么就换一个扩展名再试试。

二、通过AssetBundleName设置扩展名

意思是什么呢？就是我们在给AssetBundle包设置名字的时候，同时加入扩展名。

假如说，我们给AssetBundle包取名字叫做“MyAssetBundle”，那么这个时候，我们把名字换成“MyAssetBundle,assetbundle”，不用再设置扩展名，直接打包，我们会看到打包出来的AssetBundle包带上了扩展名。

其实这是一种讨巧的方式。用这种方式可以设置任何扩展名，都没有问题，而且可以被正确加载。

三、通过AssetBundleBuild.assetBundleVariant设置扩展名

兴许在我心里这种方式设置扩展名才是正统，也不知道为什么会有这种奇怪的念头。

我们可以在上一教程的代码基础上加上这样一句话↓↓

buildMap.assetBundleVariant = "assetbundle";

然后点击菜单，运行打包程序，虽然最后打包成功了，编辑器会报错，错误信息是这样的↓↓

1.  
   Error: Variant folder path cannot be empty
2.  
    

这是个死活找不出原因的错，明明都打包成功了，哪里报的错？？逗我来了吧？？

简直让人崩溃，问度娘，度娘说：我不知道...

哎，无奈之下只好问谷哥了，幸好谷哥给力了一把↓↓

总算是找到原因了，按照上图的方法添加这几行代码，再次运行打包，就不会再报错了，心好累...

但是你以为这样就完了？？那你就太年轻了...

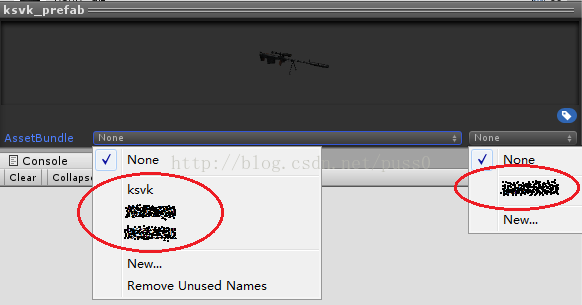
在添加了上面的代码之后，每次运行后，你设置的信息都会存储到Inspector面板中的这里↓↓还有这里↓↓

（用画图打的马赛克，将就着看吧）

也不能通过Remove Unused Names把它们删除掉，如果是处女座的话...

总结来看，最方便最保险最安全最**的设置AssetBundle后缀名的方式还是第二种方式。

最后非常非常非常感谢这位叫王思元的筒子给出的正解，它的博客里还有很多很多关于AssetBundle包和打包的知识，以及各种报错的解决方案，我只是截取了其中一段，欢迎大家去看看他的博客→→博客链接←←

下期见啦~