Python 数据结构 树

什么是树

数是一种抽象的数据类型（ADT）或是作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合，它是由n（n>1）的有限个节点和节点之间的边组成的一个有层次关系的集合。

树的组成元素：

• 根节点：树的最上层的节点，任何非空的树都有一个节点
• 路径：从起始节点到终止节点经历过的路径
• 父节点：除了根节点，每个节点的上一层边连接的节点就是它的父节点
• 子节点：每一节点由边指向的下一层节点
• 兄弟节点：同一父节点且处在同一层的节点
• 子树：每个节点包含它所有的后代组成的子树
• 叶子节点：没有子节点的节点，称为叶子节点
• 树的高度或深度：树中节点的最大层次

树具有以下的特点：

• 每个节点有零个或多个子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树。

树的种类

• 无序树：树中的任意节点的子节点之间没有顺序关系，也称为自由树。
• 有序树：树中的任意节点的子节点之间有顺序关系。
• 二叉树：每个节点最多含有两个子树
• 完全二叉树：当一个高度为h的完美二叉树减少到h-1，并且最底层的槽被毫无间隙地从左到右填充，我们就叫它完全二叉树
• 满二叉树：如果每个内部节点（非叶子节点）都有两个子节点，就成为满二叉树
• 完美二叉树：当所有的叶子节点都在同一层就是完美二叉树，毫无间隙填充了h层

　　如下图所示：

　　满二叉树：

　　

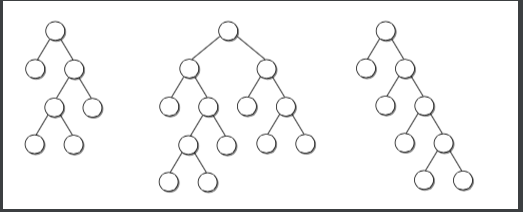
　　完美二叉树：

　　

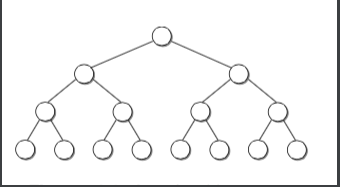
　　完全二叉树：

　　

数的存储和表示

顺序存储：将数据结构存储在固定的数组中，所以在遍历速度上有一定的优势，同时所占用的空间比较大，是非主流二叉树。二叉树通常以链式方式存储：

如下图所示是简单的顺序存储：

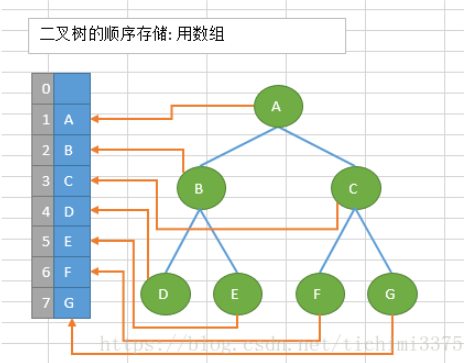
链式存储： 结构采用链表存储二叉树中的数据元素，用链表建立二叉树中节点之间关系，二叉树最常用的链式存储结构是二叉链，每个节点包含三个域，分别是数据元素域data,

左还在链域Child和右孩子链域Child，与单链表头结点和不带头节点的两种情况相似，二叉链存储结构的二叉树也有带头节点和不带头结点两种。

树的常用场景

• xml，html等，那么编写这些东西的解析器的时候，不可避免用到树
• 路由协议就是使用了树的算法
• mysql数据库索引
• 文件系统的目录结构
• 所以很多经典的AI算法其实都是树搜索，此外机器学习中的decision tree也是树结构

二叉树

二叉树的基本概念

二叉树是由n(n>=0)个节点组成的集合，每个节点最多有两个子树的有序树，它或者是空集，或者是一个根和左右子树的两个不相交的二叉树组成。

二叉树的特点：

二叉树是有序树，即使是只有一个子树，也必须区分左右树。

二叉树的每个节点的的度，不能大于2.

二叉树的遍历

前序遍历：先访问根节点， 然后前序遍历左子树，再前序遍历右子树

中序遍历：中序遍历根节点的左子树，然后再访问根节点，最后遍历右子树

后序遍历：从左到右叶子节点的方式遍历访问左子树，最后访问根节点

层序遍历：从根节点从上往下逐层遍历，在同一层，按从左到右的顺序对节点逐个访问

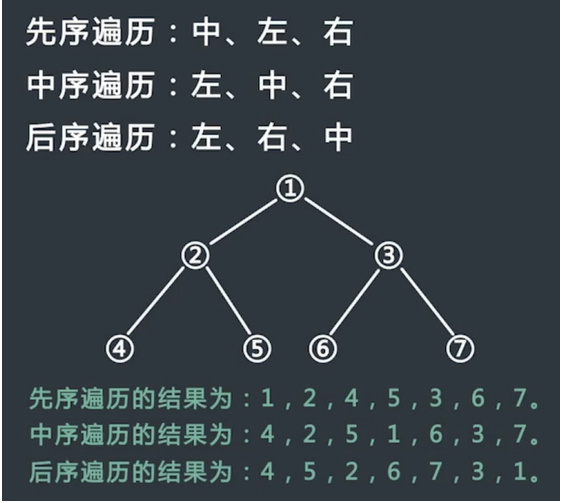
二叉树实现方式：

# 节点定义
class Node(object):
    def __init__(self, value, left_child, right_child):
        self._value = value
        self._left_child = left_child
        self._right_child = right_child

    @property
    def value(self):
        return self._value

    @value.setter
    def value(self, value):
        self._value = self.value

    @property
    def left_child(self):
        return self._left_child

    @left_child.setter
    def left_child(self, value):
        self._left_child = value

    @property
    def right_child(self):
        return self._right_child

    @right_child.setter
    def right_child(self, value):
        self._right_child = value

# 树的定义
class Tree(object):
    def __init__(self, value):
        self._root = Node(value, None, None)

    @property
    def root(self):
        return self._root

遍历树的代码实现：以下遍历方式亲测有效

# 递归后续遍历

def pre_order(root):
    if not isinstance(root, Node):
        return []
    pre_order_tmp = []
    if root is not None:
        pre_order_tmp.append(root.value)
        pre_order_tmp += pre_order(root.left_child)
        pre_order_tmp += pre_order(root.right_child)
    return pre_order_tmp

# 非递归后续遍历
def pre_order_not_recursion(root):
    if not isinstance(root, Node):
        return None
    stack = [root]
    result = []
    while stack:
        node = stack.pop(-1)
        if node:
            if isinstance(node, Node):
                result.append(node.value)
                stack.append(node.right_child)
                stack.append(node.left_child)
            else:
                result.append(node)
    return result

# 递归中序遍历
def middle_order(root):
    if not isinstance(root, Node):
        return []
    middle_order_tmp = []
    if root is not None:
        middle_order_tmp += middle_order(root.left_child)
        middle_order_tmp.append(root.value)
        middle_order_tmp += middle_order(root.right_child)
    return middle_order_tmp

# 非递归中序遍历
def middle_order_not_recursion(root):
    if not isinstance(root, Node):
        return None
    stack = [root.right_child, root.value, root.left_child]
    result = []
    while stack:
        node = stack.pop(-1)
        if node:
            if isinstance(node, Node):
                stack.append(node.left_child)
                stack.append(node.value)
                stack.append(node.right_child)
            else:
                result.append(node)
    return result

# 递归后续遍历
def post_order(root):
    if not isinstance(root, Node):
        return []

    post_order_tmp=[]
    if root is not None:
        post_order_tmp += pre_order(root.left_child)
        post_order_tmp += pre_order(root.right_child)
        post_order_tmp.append(root.value)
    return post_order_tmp

# 非递归后续遍历
def post_order_recursion(root):
    if not isinstance(root, Node):
        return None
    stack = [root.value, root.right_child, root.left_child]
    result = []
    while stack:
        node = stack.pop(-1)
        if node:
            if isinstance(node, Node):
                result.append(node.value)
                stack.append(node.right_child)
                stack.append(node.left_child)
            else:
                result.append(node)
    return result

# 分层遍历
def layer_order(root):
    if not isinstance(root, Node):
        return []

    queue = [root.value, root.left_child, root.right_child]
    result = []
    while queue:
        tmp = queue.pop(0)
        if tmp:
            if isinstance(tmp, Node):
                queue.append(tmp.value)
                queue.append(tmp.left_child)
                queue.append(tmp.right_child)
            else:
                result.append(tmp)
    return result

二叉树的其他方法：

# 递归方式计算节点个数
def node_count(root):
    if not isinstance(root, Node):
        return None
    else:
        if root:
            return node_count(root.left_child)+node_count(root.right_child)+1
        else:
            return None

# 借用分层遍历实现
def node_count_not_recursion(root):
    if not isinstance(root, Node):
        return None

    return len(layer_order(root))

# 计算二叉树深度
def tree_deep(root):
    if not isinstance(root, Node):
        return None

    if root:
        return 1+max(tree_deep(root.left_child), max(root.right_child))
    else:
        return 0

# 非递归方式实现
def tree_deep_not_recursion(root):
    if not isinstance(root, Node):
        return None

    stack = [(root, 1)]
    result = 0
    while stack:
        tmp_node, tmp_layer = stack.pop(0)
        if tmp_node:
            stack.append((tmp_node.left_child, tmp_layer+1))
            stack.append((tmp_node.ritht_child, tmp_layer+1))
            result = tmp_layer+1
    return result

# 计算第K层节点的个数
def kth_node_count(root, k):
    if not isinstance(root, Node):
        return None

    if not root or k <=0:
        return 0
    if k == 1:
        return 1
    return kth_node_count(root.left_child, k-1)+kth_node_count(root.right_child, k-1)

# 计算二叉树叶子节点的个数
def leaf_account(root):
    if not isinstance(root, Node):
        return None

    if not root:
        return 0
    if not root.left_child and not root.right_child:
        return 1
    return leaf_account(root.left_child)+leaf_account(root.right_child)

# 判断是否为二分查找树BST
# 判断是否为二分查找树BST，递归方式
# 二分查找树的定义搞清楚，二分查找树的中序遍历结果为递增序列
def is_bst_tree(root):
    if not isinstance(root, Node):
        return []

    def is_asc(order):
        for i in range(len(order)-1):
            if order[i] > order[i+1]:
                return False
        return True
    return is_asc(middle_order_not_recursion(root))

if __name__ == '__main__':
    tree = Tree(1)
    tree1 = Tree(1)
    node7 = Node(5, None,None)
    node6 = Node(4, None,None)
    node5 = Node(3, None,None)
    node4 = Node(2, None,None)
    node3 = Node(1, None,None)
    node2 = Node(3, node5, node6)
    node1 = Node(4, node3, node4)

    tree.root.left_child = node1
    tree.root.right_child = node2
    tree1.root.left_child = node2
    tree1.root.right_child = node2

    print (post_order_recursion(tree.root))

    print(is_bst_tree(tree.root))
    print(is_bst_tree(tree1.root))