POJ 3693 Maximum repetition substring（连续重复子串）

http://poj.org/problem?id=3693

题意：
给定一个字符串，求重复次数最多的连续重复子串。

思路：

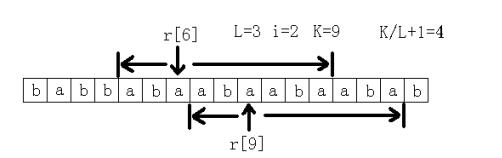
这道题确实是搞了很久，首先枚举连续子串的长度L，那么子串肯定包含了r[k]，r[k+2*L]，r[k+3*L].....（k是某个数）中相邻的两个。现在我们只需要枚举这相邻的两个，求出它们的最长公共前缀M，那么重复次数就是M/L+1。

由于要求的是字典序最小，最后再用sa数组从最前面的子串去找即可，符合条件的第一个即是答案。

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 int n;
 char s[maxn];
 int sa[maxn],t[maxn],t2[maxn],c[maxn];
 int Rank[maxn],height[maxn];
 int d[maxn][];
 int ans[maxn];

 void build_sa(int m)
 {
     int *x=t,*y=t2;
     //基数排序
     for(int i=;i<m;i++)    c[i]=;
     for(int i=;i<n;i++)    c[x[i]=s[i]]++;
     for(int i=;i<m;i++)    c[i]+=c[i-];
     for(int i=n-;i>=;i--) sa[--c[x[i]]]=i;
     for(int k=;k<=n;k<<=)
     {
         int p=;
         //直接利用sa数组排序第二关键字
         for(int i=n-k;i<n;i++)  y[p++]=i;
         for(int i=;i<n;i++)    if(sa[i]>=k)    y[p++]=sa[i]-k;
         //基数排序第一关键字
         for(int i=;i<m;i++)    c[i]=;
         for(int i=;i<n;i++)    c[x[y[i]]]++;
         for(int i=;i<m;i++)    c[i]+=c[i-];
         for(int i=n-;i>=;i--) sa[--c[x[y[i]]]]=y[i];
         //根据sa和y计算新的x数组
         swap(x,y);
         p=;
         x[sa[]]=;
         for(int i=;i<n;i++)
             x[sa[i]]=y[sa[i-]]==y[sa[i]]&&y[sa[i-]+k]==y[sa[i]+k]?p-:p++;
         if(p>=n)
             break;
         m=p;                //下次基数排序的最大值
     }
 }

 void getHeight(int n)
 {
     int i,j,k=;
     for(i=;i<=n;i++)  Rank[sa[i]]=i;
     for(i=;i<n;i++)
     {
         if(k)  k--;
         int j=sa[Rank[i]-];
         while(s[i+k]==s[j+k])  k++;
         height[Rank[i]]=k;
     }
 }

 void RMQ(int n)
 {
     for(int i=;i<=n;i++)  d[i-][]=height[i];
     for(int j=;(<<j)<=n;j++)
         for(int i=;i+(<<j)-<n;i++)
         d[i][j]=min(d[i][j-],d[i+(<<(j-))][j-]);
 }

 int query(int L, int R)
 {
     int k=;
     while((<<(k+))<=R-L+)  k++;
     return min(d[L][k],d[R-(<<k)+][k]);
 }

 int LCP(int a, int b)
 {
     int x=Rank[a],y=Rank[b];
     if(x>y)  swap(x,y);
     x--; y--;
     if(y<)  return ;
     return query(x+,y);
 }

 void solve(int n)
 {
     int MAX=-;
     int len = ;
     for(int l=;l<n;l++)   //枚举子串长度
     {
         for(int i=;i+l<n;i+=l)  //枚举起点
         {
             int k=LCP(i,i+l);
             int m=k/l+;
             int t=l-k%l;  //如果不是l的倍数，则往前几位再匹配，往后匹配已经匹配不上了
             t=i-t;
             if(t>= && k%l)
             {
                 if(LCP(t,t+l)>=k)  m++;
             }
             if(m>MAX)
             {
                 len=;
                 ans[len++]=l;
                 MAX=m;
             }
             else if(m==MAX)
                 ans[len++]=l;
         }
     }
     int l, start;  //寻找字典序最下的答案
     bool flag=false;
     for(int i=;i<=n;i++)
     {
         if(flag)  break;
         for(int j=;j<len;j++)
         {
             int tmp=ans[j];
             if(LCP(sa[i],sa[i]+tmp)>=(MAX-)*tmp)
             {
                 start=sa[i];
                 l=tmp*MAX;
                 flag=true;
                 break;
             }
         }
     }
     for(int i=start;i<start+l;i++)
         printf("%c",s[i]);

     printf("\n");
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     int kase=;
     while(~scanf("%s",s))
     {
         if(s[]=='#')  break;
         printf("Case %d: ",++kase);
         n=strlen(s);
         if(n==)  {printf("%c\n",s[]);continue;}
         n=strlen(s);
         s[n]='';
         s[n+]='\0';
         n=strlen(s);
         n++;
         build_sa();
         getHeight(n-);
         RMQ(n-);
         solve(n-);
     }
     return ;
 }