20172302 《Java软件结构与数据结构》第六周学习总结

2018年学习总结博客总目录：[第一周](https://www.cnblogs.com/hzy0628/p/9606767.html) [第二周](https://www.cnblogs.com/hzy0628/p/9655903.html) [第三周](https://www.cnblogs.com/hzy0628/p/9700082.html) [第四周](https://www.cnblogs.com/hzy0628/p/9737321.html) [第五周](https://www.cnblogs.com/hzy0628/p/9786586.html) [第六周](https://www.cnblogs.com/hzy0628/p/9825081.html)

教材学习内容总结

1.树的概述及基本概念

（1）树是一种非线性数据结构，其中的元素被组织成了一个层次结构.

（2）树由一个包含结点和边的集构成，其中元素被存储在这些结点中，边则将一个结点和另一个结点连接起来。每一结点都位于该树层次结构中的某一特顶层上。

（3）树的根式位于该树顶层的唯一结点。一棵树只有一个根结点。

（4）位于树中较底层的结点是上一层的孩子。一个结点只有一个双亲，但一个结点可以有很多孩子。同一双亲的两个结点互称兄弟（sibling）

（5）根结点是唯一没有双亲的结点。没有任何孩子的结点称为叶子，一个至少有一个孩子的非根结点称为一个内部节点。

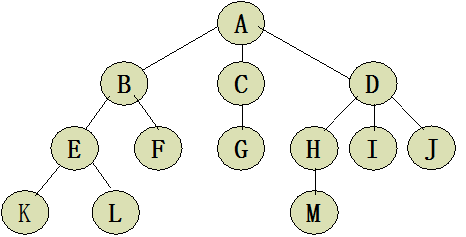
（6）一个结点在从根开始的路径中位于另一结点之上，那么该结点就是它的祖先。根是树中所有节点的最终祖先。沿着起始自某一特定结点的路径可以到达的结点是该结点的子孙（descendant）。

（7）结点的层也就是从根结点到该结点的路径长度。通过计算从根到该结点所必须穿过的边的数目，即是路径长度。根位于0层。

（8）树的高度是指从根到叶子之间最远路径的长度。

2.树的分类

树有多种分类方式，最重要的一个是树中任一结点可以具有的最大孩子的数目。这个值也称为树的度（order）。

按度来分类

对结点所含有孩子数目无限制的树称为广义树。

将每一节点限制为不超过n个孩子的树称为n元树。结点有不超过两个孩子的树称为二叉树。
按平衡来分类

（1）平衡树：树的所有叶子位于同一层或至少是彼此相差不超过一个层。

在此定义下，一个含有m个元素的平衡n元树具有的高度为log（n）m。

（2）非平衡树
按有无序分类

树中任意一个结点的各子树按从左到右是有序的，称为有序树，否则称为无序树。

一些概念

完全树

若某树是平衡的，且底层所有叶子都位于树的左边，则该树是完全的。
满树

如果一棵n元树的所有叶子都位于同一层且每一结点要么是一片叶子要么正好具有n个孩子，则该树是满的。

2.实现树的策略

（1）树的数组实现之计算策略

对于二叉树而言，一种策略是：对于任何存储在数组位置n处的元素而言，该元素的左孩子存储在位置（2n+1）处，右孩子存储在（2（n+1））处。但这样做会出现大量浪费存储空间的状况，比如这棵树不是完全的或只是相对完全的。

（2）树的数组实现之链接策略

如图：

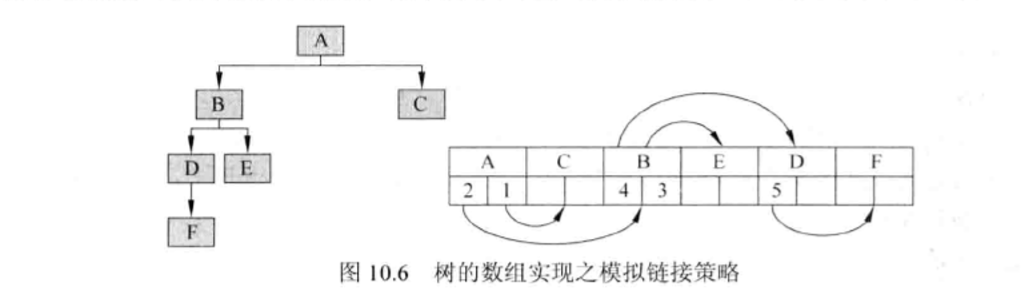
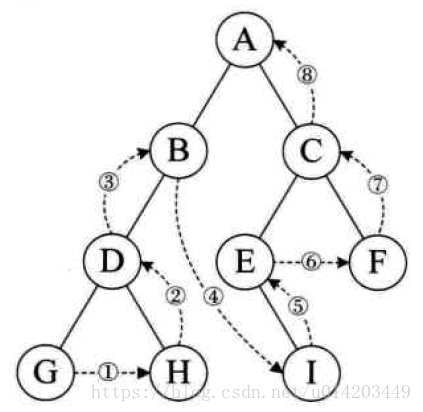
3.树的遍历

对于这样一棵树，我们对它进行四种遍历

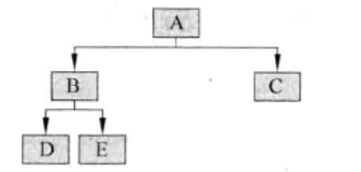
（1）前序遍历：从根节点开始，访问每一结点及其孩子

访问顺序为：A→B→D→E→C

伪代码为

Visit node

Traverse(left child)

Traverse(right child)

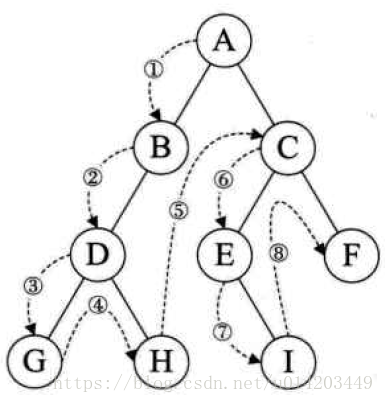
（2）中序遍历：从根结点开始，访问结点的左孩子，然后是该结点，最后是任何剩余结点

访问顺序为：D→B→E→A→C

伪代码为：

Traverse(left child)

Visit node

Traverse(right child)

（3）后序遍历：从根结点开始，访问节点的孩子，然后是该结点

访问顺序为：D→E→B→C→A

伪代码为：

Traverse(left child)

Traverse(right child)

Visit node

（4）层序遍历：从根结点开始，访问每一层的所有结点，一次一层

访问顺序为：A→B→C→D→E

4.二叉树

二叉树是树的特殊一种，具有如下特点：1、每个结点最多有两颗子树，结点的度最大为2。2、左子树和右子树是有顺序的，次序不能颠倒。3、即使某结点只有一个子树，也要区分左右子树。

特殊二叉树
- 斜树：所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树，线性表结构其实可以理解为树的一种树表达形式。
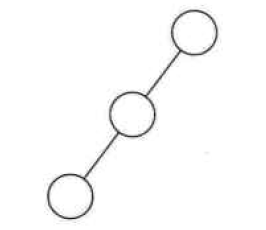
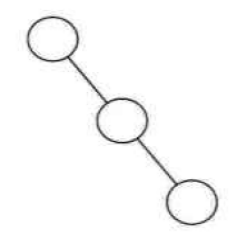
- 满二叉树：
  
  所有的分支结点都存在左子树和右子树，并且所有的叶子结点都在同一层上，这样就是满二叉树。就是完美圆满的意思，关键在于树的平衡。
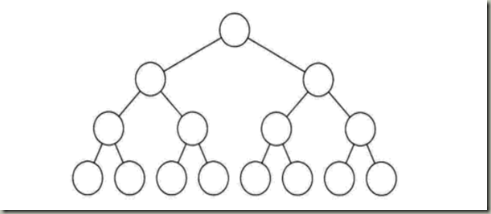
- 完全二叉树：
  
  对一棵具有n个结点的二叉树按层序排号，如果编号为i的结点与同样深度的满二叉树编号为i结点在二叉树中位置完全相同，就是完全二叉树。满二叉树必须是完全二叉树，反过来不一定成立。
二叉树的性质：

性质1：在二叉树的第i层上至多有2^i-1个结点（i>=1）。

性质2：深度为k的二叉树至多有2^k-1个结点（k>=1）。

性质3：对任何一颗二叉树T，如果其终端结点数为n0,度为2的结点数为n2，则n0 = n2+1.

性质4：具有n个结点的完全二叉树深度为[log2n]+1 ([x]表示不大于 x的最大整数)。

性质5：如果对一颗有n个结点的完全二叉树（其深度为[log2n]+1）的结点按层序编号（从第1层到第[log2n]+1层，每层从左到右），对任意一个结点i(1<=i<=n)有：

1）.如果i=1,则结点i是二叉树的根，无双亲；如果i>1,则其双亲是结点[i/2]

2）.如果2i>n,则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i。

3）.如果2i+1>n,则结点i无右孩子；否则其右孩子是结点2i+1。
二叉树的接口类——BinaryTreeADT

import java.util.Iterator;

public interface BinaryTreeADT<T>

{

    public T getRootElement();//返回二叉树根引用指向的元素

    public boolean isEmpty();//判定该树是否为空

    public int size();//判定树中元素数目

    public boolean contains(T targetElement);//判定指定目标是否在该树中

    public T find(T targetElement);//如果找到指定元素，则返回指向其的引用

    public String toString();//返回树的字符串表示

    public Iterator<T> iterator();

    public Iterator<T> iteratorInOrder();//为树的中序遍历返回一个迭代器

    public Iterator<T> iteratorPreOrder(); //为树的前序遍历返回一个迭代器

    public Iterator<T> iteratorPostOrder();//为树的后序遍历返回一个迭代器

    public Iterator<T> iteratorLevelOrder();//为树的层序遍历返回一个迭代器

}

5.使用二叉树：表达式树、背部疼痛诊断器

6.用链表实现二叉树

先要构建一个BinaryTreeNode类，它负责跟踪存储在每个位置上的元素，以及指向每个结点的左右子树或孩子的指针。然后构建实现了BinaryTreeADT接口的LinkedBinaryTree类，需要跟踪位于树的根节点，以及树的元素数目。

教材学习中的问题和解决过程

问题1：关于书上代码很难理解，尤其是Expressiontree类下的printTree()方法。
问题1解决方案：这一章的代码都不太容易看懂，关于printTree()方法我一开始想就了解它是打印树的一个方法就算了，不太愿意细扣它是怎么输出的，后面还是拿着纸把它从头到尾推了一遍，弄懂了这里，这里分享一下。

拿最简单的 1+1为例，我们知道，通过eveluate方法后，栈顶元素已经是一个树的结构了，其中存储“+”的结点是为根节点，而两个1分别是+的左结点和右结点。初始构建两个无序列表，分别存储结点、层数。创建一个当前结点，和result结果，树的高度为1（因为根结点处于第0层，其两个子结点处于第1层），可能的结点数为2^{2，因为二叉树前n层有不高于2}（n+1）个元素。继续定义当前结点数为0，进入循环。

public String printTree()

    {

        UnorderedListADT<BinaryTreeNode<ExpressionTreeOp>> nodes =new ArrayUnorderedList<BinaryTreeNode<ExpressionTreeOp>>();

        UnorderedListADT<Integer> levelList =new ArrayUnorderedList<Integer>();

        BinaryTreeNode<ExpressionTreeOp> current;

        String result = "";

        int printDepth = this.getHeight()-1;

        int possibleNodes = (int)Math.pow(2, printDepth + 1);

        int countNodes = 0;

        nodes.addToRear(root);

        Integer currentLevel = 0;

        Integer previousLevel = -1;

        levelList.addToRear(currentLevel);

        while (countNodes < possibleNodes)

        {

            countNodes = countNodes + 1;

            current = nodes.removeFirst();

            currentLevel = levelList.removeFirst();

            if (currentLevel > previousLevel)

            {

                result = result + "\n\n";

                previousLevel = currentLevel;

                for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)

                    result = result + " ";

            }

            else

            {

                for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)

                {

                    result = result + " ";

                }

            }

            if (current != null)

            {

                result = result + (current.getElement()).toString();

                nodes.addToRear(current.getLeft());

                levelList.addToRear(currentLevel + 1);

                nodes.addToRear(current.getRight());

                levelList.addToRear(currentLevel + 1);

            }

            else {

                nodes.addToRear(null);

                levelList.addToRear(currentLevel + 1);

                nodes.addToRear(null);

                levelList.addToRear(currentLevel + 1);

                result = result + " ";

            }

        }

        return result;

    }

第一次循环：countNodes=1；current=“+”所在结点，currentLevel = 0，此时currentLevel>previousLevel，result = “\n\n”，previousLevel = 0，进入循环，循环一次，result = “\n\n空”，然后current不等于null，进入，得result=“\n\n空+”，nodes中元素1所在结点、1所在结点，levelList中元素1、1。

第二次循环：countNodes=2；current=“1”所在结点，currentLevel = 1，此时currentLevel>previousLevel，result = “\n\n\空+\n\n”，previousLevel = 1，不能进入循环，result = “\n\n\n\n空+\n\n”，然后current不等于null，进入，得result=“\n\n\n\n空+\n\n1”，nodes中1所在结点、null、null，levelList中元素1、2、2。

第三次循环：countNodes=3；current=“1”所在结点，currentLevel = 1，此时currentLevel不大于previousLevel，故调用else中代码，循环次数1次，得result=“\n\n\n\n空+\n\n1空”，然后current不等于null，进入，得result=“\n\n\n\n空+\n\n1空1”，nodes中null、null、null、null，levelList中元素2、2、2、2。

第四次循环：countNodes=4；current =null，currentLevel = 2，此时currentLevel>previousLevel，result=“\n\n空+\n\n1空1\n\n”，previousLevel = 2，不能进入循环，此时current等于null，故调用else中代码，nodes中null、null、null、null、null，levelList中元素2、2、2、3、3。result=“\n\n空+\n\n1空1\n\n空”。

第五次，不能进入循环，输出结果：result=“\n\n空+\n\n1空1\n\n空”，即result=“\n\n +\n\n1 1\n\n ”。IDEA运行结果如图，与计算一致。

循环完成之后，就该试着解释每个变量的在整个打印树中的作用，nodes是用作存储树中各个结点所指向的元素，levelList是用作存储各个元素它所对应的层数位置变量，currentLevel和previousLevel共同在决定着是否该换行，即是否该跳至下一行。第一个if-else语句中循环是用作控制着空格的打印，以及该空几格。第二个if-else语句是在将该结点的子结点及其层数分别添加到nodes和levelList中去。

问题2：在运行背部疼痛诊断器时，总是出错，后面才发现循环不能进行。
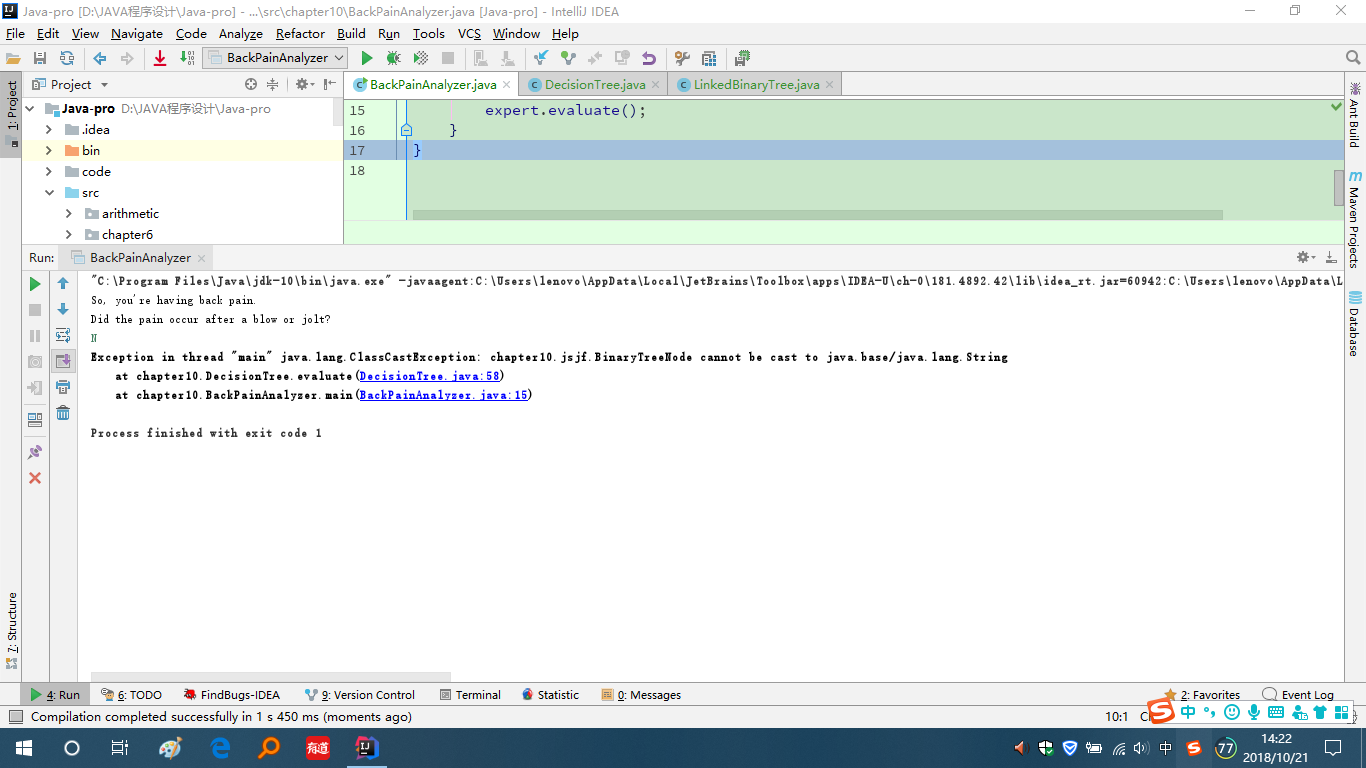
问题2解决方案：这里进行了一次之后，循环就会跳出，于是我就设置一个显示，显示当前current的size()，发现if (scan.nextLine().equalsIgnoreCase("N"))current = current.getLeft(); else current = current.getRight();运行后current.size()变为1，这里可以看出应该是getLeft和getRight方法有问题，于是找到LinkedBinaryTree中的对应方法：

public LinkedBinaryTree<T> getLeft()

    {

        return  new LinkedBinaryTree(this.root.getLeft());

    }

public LinkedBinaryTree<T> getRight()

    {

        return  new LinkedBinaryTree(this.root.getRight());

    }

这个代码是从那里直接拿过来的，以为它是对的，也就没有改动，再看才发现问题，按照这个代码相当于是在取出root的左右孩子的结点元素，然后再拿它创建一个新的LinkedBinaryTree类的对象，这就是没有了之前的树的结构了，只是单单取出这一个结点元素创建新对象返回。而这样，显然，它是没有之前本该有的孩子了。知道了是这样，就把这个方法做了修改，如图，(是修改的那部分)

protected LinkedBinaryTree<T> left,right;//定义两个LinkedBinaryTree类型的初始变量left、right

// 修改构造函数，初始化两个变量

public LinkedBinaryTree(T element, LinkedBinaryTree<T> left,

                            LinkedBinaryTree<T> right)

    {

        root = new BinaryTreeNode<T>(element);

        root.setLeft(left.root);

        root.setRight(right.root);

        this.left = left;

        this.right = right;

    }

//修改后的方法

public LinkedBinaryTree<T> getLeft()

    {

        return left;

    }

    public LinkedBinaryTree<T> getRight()

    {

       return right;

    }

改完之后，问题就解决了。

代码调试中的问题和解决过程

问题1：书上的“使用二叉树：表达式树”这里想要运行书上的代码，需要自己在LinkedBinaryTree类中添加getHeight()方法，遇到的问题见下：
问题1解决方案：在我补全了getHeight()方法后，再去运行程序，始终会抛出错误StackOverflowError，查API文档

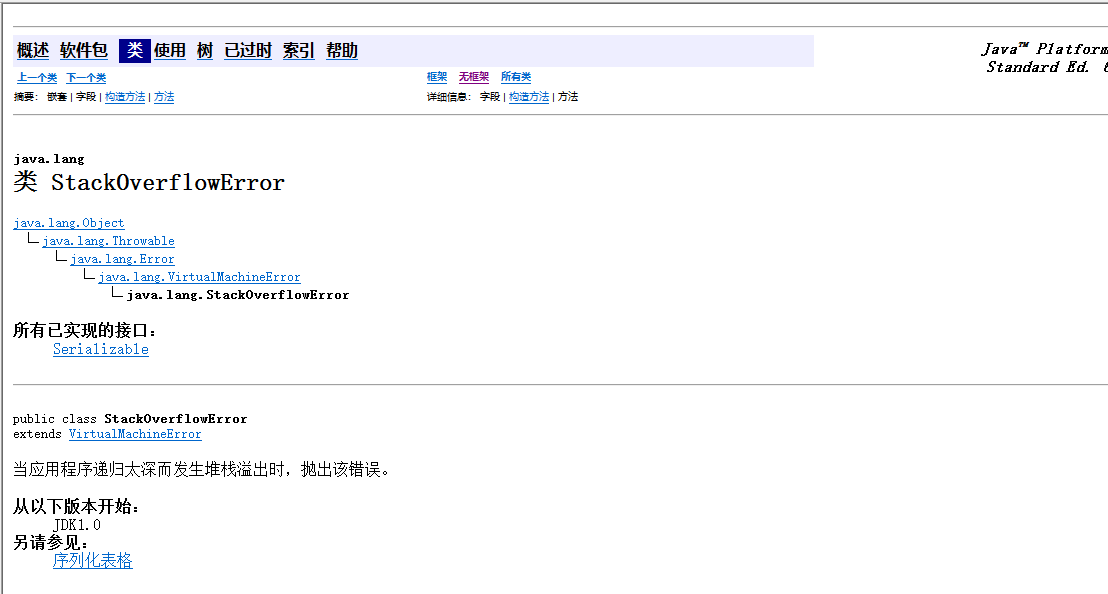
注意到了“当应用程序递归太深而发生堆栈溢出时，抛出该错误”，但不明白什么叫递归太深。就又搜索了这个错误。

StackOverflowError是由于当前线程的栈满了，也就是函数调用层级过多导致。

比如死递归。

以上是网上查阅的资料。

死递归，这个知道一些，就是递归无法挑出来，if条件给的不对，于是就从递归下手，认真看了两遍，找到了错误。

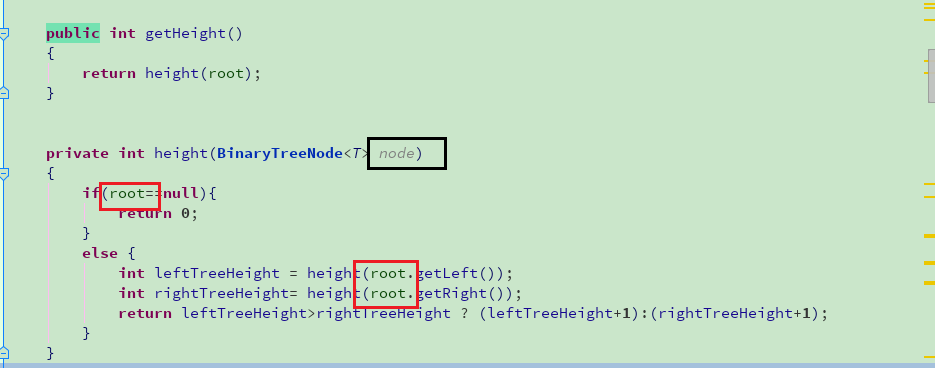
圈红地方就是出错的地方，每次的递归我都是在用root这个，根本无法跳出递归，将root改为node，即可运行。

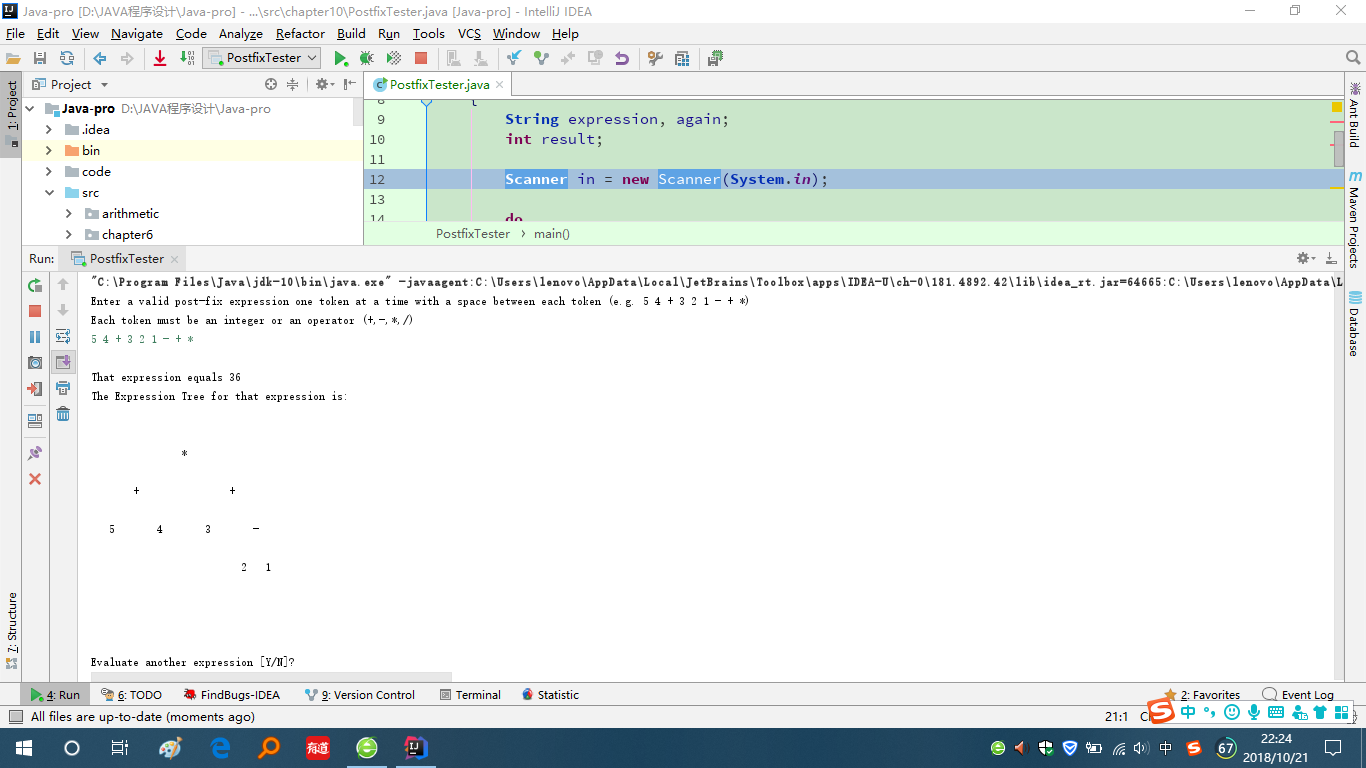
问题2：在测试contains方法时，它始终的结果是false，明明包含该元素也会显示为false。
问题2解决方案：如图，进行了单步调试，可以看出next.getElement()和targetElement中元素均为“+”，可是却判定条件不成立。

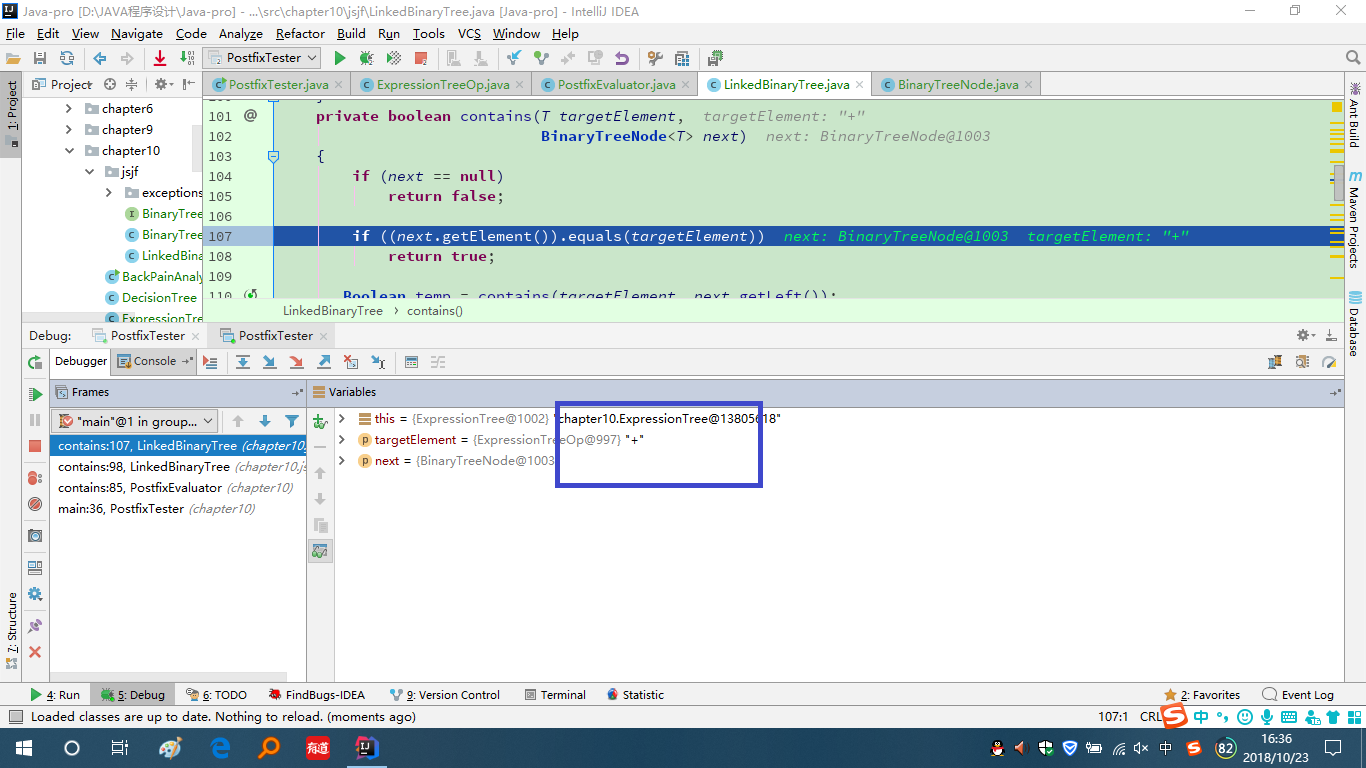
抱着试一试的心态，就把next.getElement()和targetElement都使用了String.valueOf()，输出的就是true了，可能是因为之前的元素类型不同吧，或者可以在next.getElement()前加个强制类型转换，转换为T，试了一下返回的结果又变回false了，有点奇怪。

代码托管

上周代码行数为11412行，现在为12499行，本周共1087行。

上周考试错题总结

上周未进行考试

结对及互评

本周结对学习情况
- 20172308
- 博客中值得学习的或问题：
- 结对学习内容：第十章——树。

其他（感悟、思考等）

感悟

树这一章可以感觉是到目前为止学起来最为困难的一章，一开始看表达式树时，整个都是混乱的，因为它调用后面的链表创建树，包括表达式树中的方法，理解起来都有困难。后面靠看着UML类图，对整个结构才算明白了一些，然后才去试着把每个类下面的方法弄明白。最为困惑的就是背部疼痛诊断器，它是从文件中读取，然后输出，可是我弄了好久它就只能输出一个问题，循环不了，这里还是有问题。下一章依然与树有关，希望能把树这一部分完全弄懂。

同时本周对博客园的博客样式进行了较大的改动。不改感觉不好看，改起来又很麻烦，最后改这一次了。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	0/0	1/1	15/15
第二周	572/572	1/2	16/31
第三周	612/1184	1/3	13/44
第四周	1468/2652	2/5	13/57
第五周	1077/3729	1/6	14/71	初步理解各个排序算法
第六周	1087/4816	1/7	17/88	认识树结构

参考资料