manifold learning

MDS, multidimensional scaling, 线性降维方法, 目的就是使得降维之后的点两两之间的距离尽量不变（也就是和在原是空间中对应的两个点之间的距离要差不多）。只是 MDS 是针对欧氏空间设计的，对于距离的计算也是使用欧氏距离来完成的。如果数据分布在一个流形上的话，欧氏距离就不适用了。

1. 所谓 Machine Learning 里的 Learning ，就是在建立一个模型之后，通过给定数据来求解模型参数。

2. Riemannian geometry;

from here.

黎曼空间就是弯曲的空间, 而欧氏空间只算是黎曼空间的一种特例。

在黎曼空间里，坐标线不一定是直的，坐标线的尺规可以不是单位1（可以每个地方都不同），坐标线之间也不一定是垂直的。

流形：流形是啥呢？大家知道足球吧，就那个黑白花纹的，一块一块皮缝出来的球形物体。其实每一块皮基本上都是平的（就是你能理解的那种“平”），但是缝起来就是个足球。流形也是一样，它的比较数学化的表述是，有一个点组成的集合M，M中每一个点的附近都有一个邻域，那个邻域和欧式空间“长”的差不多（数学术语叫同胚，很形象的一个词）。还是刚刚的足球，足球上每一个点都在某块皮上，那块皮扯下来就是个平坦的东西。

直观上来讲，一个流形好比是一个 d 维的空间，在一个 m 维的空间中 (m > d) 被扭曲之后的结果。需要注意的是，流形并不是一个“形状”，而是一个“空间”，如果你觉得“扭曲的空间”难以想象，那么请再回忆之前一块布的例子。

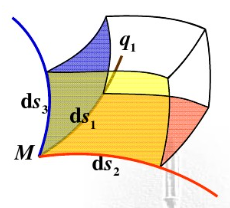
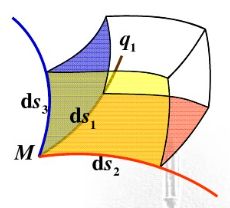
当然，这些都是直观上的概念，其实流形并不需要依靠嵌入在一个“外围空间”而存在，稍微正式一点来说，一个 d 维的流形就是一个在任意点出局部同胚于（简单地说，就是正逆映射都是光滑的一一映射）欧氏空间  。实际上，正是这种局部与欧氏空间的同胚给我们带来了很多好处，这使得我们在日常生活中许许多多的几何问题都可以使用简单的欧氏几何来解决，

度量: 其实度量从它名字来看就能理解，度量度量，就是量一量长度嘛。人类规定了单位米尺的长度，所以我们就可以度量北京到上海的距离，可以度量你一根手指的长度，一根发丝的长度。对于这种规定了怎么量长度的空间，数学上称为度量空间。而我们最熟悉的那种量长度的方式（其实你只知道这一种，相信我），称为欧氏度量。一个例子就是初中的二维的笛卡尔坐标，两个点之间的距离就是他们横纵坐标的差平方和再开方，那就是二维的欧式度量，也是我们认为最自然的度量。但是（凡事都要有个但是），度量并不是唯一的，就是说还存在其他量距离的方式。事实上有无穷多种方式来量，但是它们之中有很多是很无聊的，大家不去研究它们.

事实上，欧氏空间也不过是一种特殊的流形，流形才是最本质的概念。黎曼在一般的流形上定义了一类特殊的度量（就是规定了一种特殊的但是会比较有意思的怎么量距离的方式），我们称为黎曼度量。有了黎曼度量，我们就可以研究这个流形到底是不是弯的？有多弯？我们可以研究上面的“直线”是什么东西，从而我们可以研究怎么才能最短的从一个点到另一个点。

流形没有坐标轴，它的坐标都是局部的。

在流形空间的直线： 测地线。如何测量曲线长度：一条曲线的长度，就是通过它每一点 切向量大小 的积分得到的。

而流形上的“直线”，其实就是这两点间距离最短的那条曲线。既然这么一条曲线是最短的，那我们知道在它周围生活的曲线们都比它长，所以在连接这两个点的所有曲线生活的空间上定义一个函数叫做 求曲线长度函数，那么我们的测地线就是这个 求曲线长度函数 的最小值点。一般来说数学上对于这种最小值，最大值的点，都有办法描述他们，通常是用一些方程来描述。于是，我们的测地线的定义的终极版本粗线了：就是满足某一组特定方程的流形上的曲线。

最短的是测地线，测地线不一定是最短的。

其实很简单，想象一下，你要从北京飞到上海，结果你先从北京飞到了北极，然后越过北极沿着经线继续飞到了南极，再越过南极回到上海。这条路径是大圆上的一段弧，自然是测地线，可是！假如你真这么干……你还说自己走的路最短……我就不做评价了……

测地线是局部最短的。

3. 莫比乌斯环和克莱因瓶

莫比乌斯环是只有一面的曲目。

克莱因瓶：一条边没有，是一个完整的曲面。 克莱因瓶其实在我们的世界里并不存在，存在于四维空间，

References:

Riemannian Geometry:

1. 浅谈流形学习
2. Zero谈数学——黎曼几何(1)

3. Zero谈数学——黎曼几何（2）

4. Zero谈数学——黎曼几何（3）

5. 神奇的克莱因瓶和莫比乌斯环