Lindström–Gessel–Viennot lemma定理 行列式板子

https://blog.csdn.net/qq_37025443/article/details/86537261 博客

下面是wiki上的讲解，建议耐心地看一遍...虽然看了可能还是不懂

https://en.wikipedia.org/wiki/Lindström–Gessel–Viennot_lemma

Lindström–Gessel–Viennot lemma定理是

起点集合A=(a1,a2,a3..an)，终点集合B=(b1.b2,b3,..bn)

假定P是从一条从一个点到另一个点的路径，定义w(P)=路径上经过的边的权值积

定义一个n元组P‘=(P1,P2,P3...PN)

Pi: -> 的路径

是{1,2,3,...n}的一种排列(类似于置换群的概念)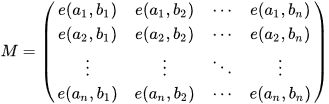

M行列式所求的值代表...(那句话我也不知道怎么翻译直接看原文吧)

下面这句话就是讲我们真正的用处——当所有边的权值都为1，并且 只有一种排列组合是可以的(即ai->bi)

那么M计算出来的值就是ai->bi不相交路径的方案数。此时e(a,b)就是a->b的合法路径的方案数

看了上面你可能还是不懂，其实在实际题目中用一下，你就可以知道他的套路了

Intersection is not allowed!
Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 602    Accepted Submission(s): 195

Problem Description

There are K pieces on the chessboard.

The size of the chessboard is N*N.

The pieces are initially placed on the top cells of the board.

A piece located on (r, c) can be moved by one cell right to (r, c + 1) or one cell down to (r+1, c).

Your task is to count how many different ways to move all pieces to the given positions at the bottom of the board.

Furthermore, the paths of the pieces mustn’t intersect each other.

Input

The first line of input contains an integer T-the number of test cases.

Each test case begins with a line containing two integers-N(1<=N<=100000) and K(1<=K<=100) representing the size of the chessboard and the number of pieces respectively.

The second line contains K integers: 1<=a1<a2< …<aK<=N representing the initial positions of the pieces. That is, the pieces are located at (1, a1), (1, a2), …, (1, aK).

Next line contains K integers: 1<=b1<b2<…<bK<=N representing the final positions of the pieces. This means the pieces should be moved to (N, b1), (N, b2), …, (N, bK).

Output

Print consecutive T lines, each of which represents the number of different ways modulo 1000000007.

Sample Input

1

5 2

1 2

3 4

Sample Output

50

题意:

给你一个n*n的矩阵，再第一行一次有k个起点1<=a1<a2<a3<...<ak<=n

最后一行有n个终点1<=b1<b2<b3<...<bk<=n

你只能向右或向下走，问你有多少种路线方案，使得ai->bi  i=1...n

答案mod 1e9+7

解析:

e(a,b)是合法路径的方案数，那么我们就先将这个行列式填好

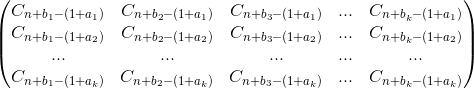
然后我们只需要用高斯消元法求出这个行列式的值就可以得出答案了。

也就是把通过行列式行变换把行列式转换成上(下)三角矩阵，然后将对角线上的元素乘起来就是答案了

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long int ll;

const int MAXN = 2e5+;
ll jc[MAXN];
ll inv[MAXN];

const ll MOD = 1e9+;
const int N = 1e2+;
ll a[N][N];

ll pow(ll a, ll n, ll p)    //快速幂 a^n % p
{
    ll ans = ;
    while(n){
        if(n & ) ans = ans * a % p;
        a = a * a % p;
        n >>= ;
    }
    return ans;
}

ll niYuan(ll a, ll b)   //费马小定理求逆元
{
    return pow(a, b - , MOD);
}

inline ll C(int a, int b)    //计算C(a, b),a下，b上
{
    if(b>a) return ;
    return jc[a] * inv[b] % MOD
        * inv[a-b]%MOD;
}

void init()
{
    ll p=;
    jc[]=;
    jc[]=;
    inv[]=;
    inv[]=;
    for(int i=;i<MAXN;i++){
        p=(p*i)%MOD;
        jc[i]=p;
        //inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;
    }

    for(int i=;i<MAXN;i++) inv[i]=inv[MOD%i]*(MOD-MOD/i)%MOD;   //O(n)求逆元
    for(int i=;i<MAXN;i++) inv[i]=inv[i-]*inv[i]%MOD;   //扩展到i!的逆元
}

ll determinant(int n)
{
    //a为方阵
    //MOD根据实际情况而定
    ll ans=;
    for(int k=;k<=n;k++)  //将a[k+1..n][k]都变成0
    {
        ll pos=-;
        for(int i=k;i<=n;i++)  //找到a[k..n][k]中第一个非0元素
            if(a[i][k])
            {
                pos=i;
                break;
            }
        if(pos==-)return ;  //没有的话行列式值为0
        if(pos!=k)  //将找到的那一行换到第k行，swap(a[k],a[pos])
            for(int j=k;j<=n;j++)swap(a[pos][j],a[k][j]);
        ll inv=niYuan(a[k][k],MOD);
        for(int i=k+;i<=n;i++)
            if(a[i][k])
            {
                ans=ans*inv%MOD;   //下面的计算中第i行提高a[k][k]倍，所以答案需要除以a[k][k]才是正解
                for(int j=k+;j<=n;j++)
                    a[i][j]=((a[i][j]*a[k][k]%MOD-a[k][j]*a[i][k]%MOD)%MOD+MOD)%MOD;
                a[i][k]=;
            }
    }
    for(int i=;i<=n;i++)
        ans=ans*a[i][i]%MOD;
    return ans;
}

int A[N],B[N];

int main()
{
    int t;
    init();
    scanf("%d",&t);
    while (t--)
    {
        int n,k;
        scanf("%d%d",&n,&k);
        for(int i=;i<=k;i++) scanf("%d",&A[i]);
        for(int i=;i<=k;i++) scanf("%d",&B[i]);

        for(int i=;i<=k;i++)
        {
            for(int j=;j<=k;j++)
            {
                a[i][j]=C(n+B[j]-(+A[i]),n-);
            }
        }
        printf("%lld\n",determinant(k));
    }
}

https://blog.csdn.net/qq_36368339/article/details/81133921

题意：给你一个矩阵(#表示不可走)，两只乌龟从左上角出发到达右下角，中间不能相遇，存在多少种不同的方案，也就是两条不相交的路径的方案数.
分析：
LGV：(https://en.wikipedia.org/wiki/Lindstr%C3%B6m%E2%80%93Gessel%E2%80%93Viennot_lemma)
ps：我自己也不是很懂原理，但是知道怎么用，就说一下吧.
给定n个起点，n个终点(一个终点对应一个起点)，LGV主要解决n∗nn∗n条路径不相交的方案数.
LGV是一个n阶的行列式，行代表起点，列代表终点，(i, j)表示第i个起点到第j个终点的方案数，最后行列式的值就是n条不相交路径的方案数.

有了LGV，这个题最大的麻烦解决了。两只乌龟同起点同终点，要分离出来，也就等价一只乌龟从(1, 2)出发，到(n - 1, m)，另一只从(2, 1)到(n, m - 1)，因为路径不相交，不懂得可以仔细想想。
有了起点，有了终点，每个起点对应每个终点的方案数，用DP转移一下行了，然后就套LGV问题解决.
相当于两个起点，两个终点的题，且起点的横坐标都是1，终点的横坐标都是n。

#include <stdio.h>
#include <cstring>
typedef unsigned long long LL;

const int MAXN = 3e3 + ;
const int mod = 1e9 + ;
LL dp[MAXN][MAXN];
char ma[MAXN][MAXN];

int main() {
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = ; i <= n; ++i) {
        getchar();
        for(int j = ; j <= m; ++j) {
            ma[i][j] = getchar();
        }
    }
    if(ma[][] == '#' || ma[][] == '#') {
        puts("");
        return ;
    }
    if(ma[][] != '#') dp[][]++;
    for(int i = ; i <= n; ++i) {
        for(int j = ; j <= m; ++j) {
            if(ma[i][j] != '#') dp[i][j] = (dp[i][j] + dp[i - ][j] + dp[i][j - ]) % mod;
        }
    }
    LL ans1 = dp[n - ][m] % mod, ans2 = dp[n][m - ] % mod;
    memset(dp, , sizeof(dp));
    if(ma[][] != '#') dp[][]++;
    for(int i = ; i <= n; ++i) {
        for(int j = ; j <= m; ++j) {
            if(ma[i][j] != '#') dp[i][j] = (dp[i][j] + dp[i - ][j] + dp[i][j - ]) % mod;
        }
    }
    LL ans3 = dp[n - ][m] % mod, ans4 = dp[n][m - ] % mod;
    printf("%lld\n", ((ans4 * ans1) % mod - (ans2 * ans3) % mod + mod) % mod);
    return ;
}

https://blog.csdn.net/ftx456789/article/details/81132126

牛客上的一个题。